Geometria Plana
Matemática
A geometria plana é a área de estudos que se volta para os objetos pertencentes ao plano, ou seja, todos os seus elementos (ponto, reta e polígonos) estão “dentro” do plano. A geometria teve seu início na Grécia Antiga e é conhecida também como geometria euclidiana plana, em homenagem a um grande estudioso da área chamado Euclides. Matemático de Alexandria, Euclides é conhecido como o “pai da geometria”.
Leia também: Geometria espacial – estudo das figuras com três dimensões
Conceitos da geometria plana
Alguns conceitos são essenciais para que se entenda a geometria plana, mas não são demonstráveis, sendo chamados de conceitos primitivos. São eles:
-
Ponto
O ponto não possui dimensão e vamos representá-lo por uma letra maiúscula.
-
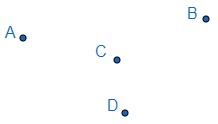
Reta
A reta possui uma dimensão, o comprimento, e é representada por uma letra minúscula. A reta é infinita.
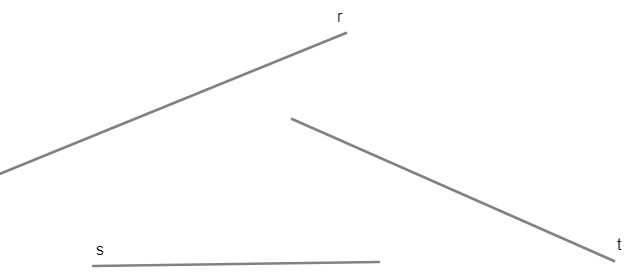
A partir do conceito de reta, podemos definir três outros conceitos: segmento de reta, semirreta e ângulo.
– Segmento de reta
O segmento de reta é definido por uma reta delimitada por dois pontos distintos, ou seja, uma reta com começo e fim.
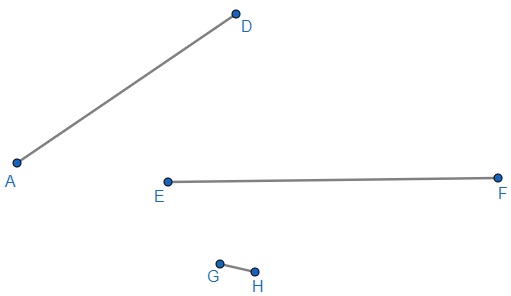
– Semirreta
A semirreta é definida como sendo uma reta com começo e sem fim, ou seja, ela será infinita em uma das direções.
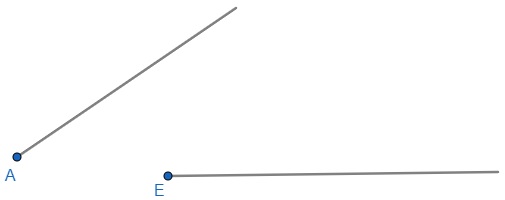
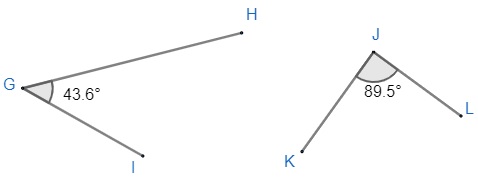
– Ângulo
O ângulo é utilizado para medir o espaço entre duas retas, semirretas ou segmentos de retas. Quando medimos um ângulo, estamos determinando sua amplitude.
-
Plano
O plano apresenta duas dimensões e é representado por uma letra grega (α, β, γ, … ).
Veja também: Ponto, reta, plano e espaço: fundamentos da geometria plana
Fórmulas e figuras principais da geometria plana
Agora veremos as principais fórmulas para calcular áreas de figuras planas.
-
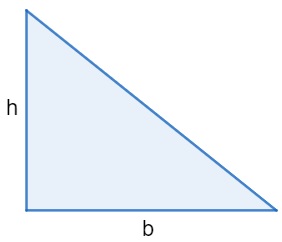
Triângulo
Para calcular a área de um triângulo, basta multiplicar a medida da base (b) com a medida da altura (h) e dividir o resultado por dois.
-
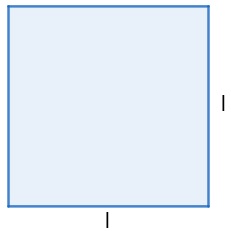
Quadrado
Sabemos que os lados do quadrado são todos iguais. Para calcular sua área, multiplicamos a medida da base com a medida altura. Como as medidas são as mesmas, multiplicá-las é o mesmo que elevar o lado ao quadrado.
-
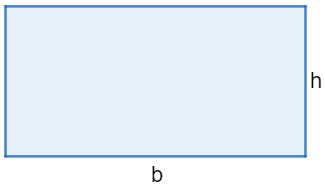
Retângulo
A área do retângulo é dada pela multiplicação da base pela altura.
-
Losango
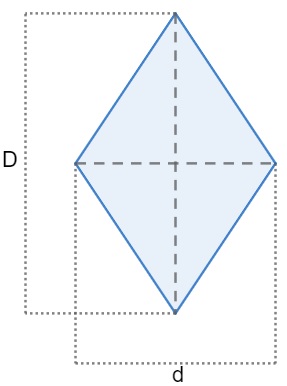
A área do losango é dada pelo produto da diagonal maior (D) com a diagonal menor (d) dividido por dois.
-
Trapézio
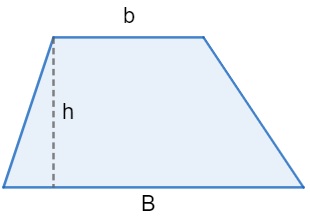
A área do trapézio é dada pelo produto da altura com a soma da base maior (B) e a base menor (b) dividido por dois.
-
Círculo
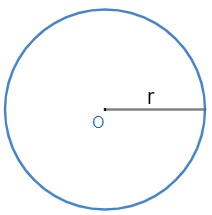
A área do círculo de raio r é dada pelo produto do raio ao quadrado com o número irracional ℼ (em geral utilizamos o valor ℼ = 3,14).
Veja também: Área dos sólidos geométricos – fórmulas e exemplos
Geometria plana e espacial
A geometria plana é caracterizada por ter todos os seus elementos contidos no plano. Assim, nenhum objeto na geometria plana tem volume, e sim área. Mas o mundo real não possui apenas duas dimensões, certo? Você, neste exato momento, consegue se mexer para frente e para trás (uma dimensão), para a direita e para a esquerda (mais uma dimensão) e, por fim, girar em uma cadeira de escritório (mais uma dimensão), ou seja, três dimensões.
A geometria espacial trata de estudar justamente objetos que estão na terceira dimensão. Algumas das estruturas estudadas na geometria espacial estão presentes em nosso dia a dia, como esferas, cones, cilindros e paralelepípedos.
Geometria plana no Enem
A geometria plana possui diversas aplicações em nosso cotidiano. Em razão da vasta aplicabilidade, existe uma gama de problemas que podem ser explorados e, consequentemente, esse assunto aparece com frequência em questões de vestibulares e Enem.
Questões de geometria plana exigem do aluno um raciocínio construtivo e lógico. A grande dificuldades das questões não é com os conceitos geométricos em si, e sim com o envolvimento de temas como equação do primeiro grau, equação do segundo grau, operações com frações, porcentagem e proporção. Vejamos alguns exemplos.
→ Exemplo 1
(Enem/2012) Em 20 de fevereiro de 2011, ocorreu a grande erupção do vulcão Bulusan nas Filipinas. A sua localização geográfica no globo terrestre é dada pelo GPS com longitude de 124° 3’ 0’’ a leste do Meridiano de Greenwich. (Dado: 1° equivale a 60’ e 1 equivale a 60″.)
PAVARIN, G. Galileu, fev. 2012 (adaptado)
A representação angular da localização do vulcão com relação a sua longitude de forma decimal é:
a) 124,02°
b) 124,05°
c) 124,20°
d)124,30°
e)124,50°
Solução
Para resolver o exercício, devemos transformar 124° 3’ e 0″ (lê-se: cento e vinte e quatro graus, três minutos e zero segundos) para graus. Para isso, basta escrevermos os 3 minutos em graus e, já que a localização possui 0″, não há nada a fazer.
Foi fornecido pelo exercício que 1° equivale a 60’. Vamos utilizar uma regra de três simples para determinar quantos graus temos em 3 minutos.
1° – – – 60’
x° – – – 3’
60x = 3
x = 3 ÷ 60
x = 0,05°
Assim, 124° 3’ e 0″ é equivalente a escrever:
124° + 0,05° + 0°
124,05°
Resposta: alternativa b.
→ Exemplo 2
(Enem/2011) Uma escola tem um terreno vazio no formato retangular cujo perímetro é de 40 m, onde se pretende realizar uma única construção que aproveite o máximo de área possível. Após a análise realizada por um engenheiro, este concluiu que, para atingir o máximo de área do terreno com uma única construção, a obra ideal seria:
a) um banheiro com 8 m2.
b) uma sala de aula com 16 m2.
c) um auditório com 36 m2.
d) um pátio com 100 m2.
e) uma quadra com 160 m2.
Solução
Como desconhecemos as dimensões do terreno retangular, vamos nomeá-las por x e y.
De acordo com o enunciado, o perímetro é igual a 40 m, ou seja, a soma de todos os lados é igual a 40 m, logo:
x + x + y + y = 40
2x + 2y = 40
2(x +y) = 40
x + y = 20
y = 20 – x
Sabemos também que a área de um retângulo é dada pelo produto da base com a altura, assim:
A = x · y
Substituindo o valor de y, isolado anteriormente, temos:
A = x · (20 – x)
A = – x2 + 20x
Agora, para sabermos qual é a área máxima, basta determinar o valor máximo da função A, ou seja, determinar o vértice da parábola. O valor de xv é dado por:
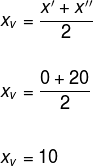
Para determinar o valor do yv, vamos substituir o valor de xv na função A.
A = – x2 + 20x
A = – (10)2 + 20(10)
A = – 100 + 200
A = 100 m2
Portanto, a área máxima é de 100 m2.
Resposta: alternativa d.
Exercícios resolvidos
Questão 1 – Sabendo que área do trapézio abaixo é de 18 m2, determine o valor de x.
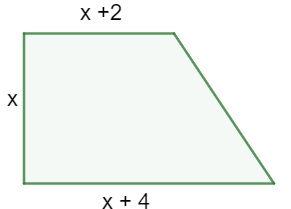
Resolução
Como a área é igual a 18 m2, podemos substitui-la na fórmula da área do trapézio, bem como os valores das medidas dados pelo problema. Veja:
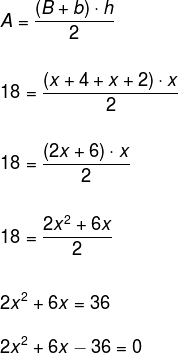
Solucionando agora a equação do segundo grau, temos:
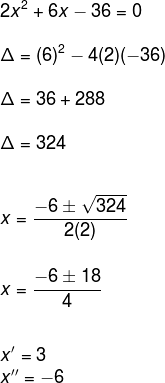
Note que o valor de x no problema retrata uma medida de comprimento, logo só pode assumir um valor positivo, portanto:
x = 3
Questão 2 – Calcule a área do losango que possui a diagonal maior como o dobro da menor.
Resolução
Como desconhecemos os valores das diagonais, vamos nomeá-las por x.
Diagonal menor (d) → x
Diagonal maior (D) → 2x
E substituindo essas informações na fórmula, temos:
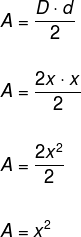
Por Robson Luiz
Professor de Matemática
Artigos Geometria Plana
.jpg "Teorema de Tales")
.jpg "Medidas")
.jpg "Teorema de Tales")
Proibida a reprodução total ou parcial sem prévia autorização (Inciso I do Artigo 29 Lei 9.610/98)