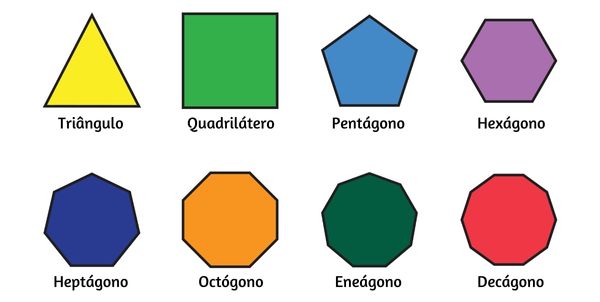
Polígono regular

Polígono regular é o polígono convexo que possui todos os lados congruentes e todos os ângulos internos congruentes, ou seja, os lados possuem a mesma medida e os ângulos internos também possuem a mesma medida. O triângulo equilátero e o quadrado são alguns dentre os polígonos regulares conhecidos.

Leia também: Quais são os elementos de um polígono?

Tópicos deste artigo

• 1 - Resumo sobre polígono regular
• 2 - Videoaula sobre polígonos regulares
• 3 - O que são polígonos regulares?
• 4 - Perímetro do polígono regular
• 5 - Ângulos internos de um polígono regular
• 6 - Ângulos externos de um polígono regular
• 7 - Apótema do polígono regular
• 8 - Área do polígono regular
• 9 - Diferença entre o polígono regular e o polígono irregular
• 10 - Exercícios sobre polígono regular

Resumo sobre polígono regular

• Polígono regular é aquele que possui lados e ângulos congruentes.

• O perímetro de um polígono regular é o comprimento do lado vezes a quantidade de lados:

\(P = n ⋅l \)

• A medida de cada ângulo interno do polígono regular é dada pela seguinte fórmula:

\(α=\frac{S_i}n\)

• A medida do ângulo externo de um polígono regular é dada pela seguinte fórmula:

\(e=\frac{360}n\)

• O apótema de um polígono regular é igual à medida do raio de uma circunferência circunscrita.

• A área de um polígono regular é dada pela seguinte fórmula:

\(A=a⋅p\)

• Enquanto o polígono regular possui todos os seus lados e ângulos congruentes, o polígono irregular não possui todos os lados congruentes ou não possui todos os ângulos congruentes.

Videoaula sobre polígonos regulares

O que são polígonos regulares?

Polígonos regulares são os polígonos convexos que são equiláteros e equiângulos, ou seja, possuem lados congruentes e também possuem ângulos com a mesma medida. Lembre-se que polígonos são convexos quando qualquer segmento de reta que possui extremidades em seu interior está totalmente contido no polígono. O triângulo equilátero e o quadrado são casos de polígonos regulares, mas há pentágonos, hexágonos, entre outros polígonos que também são regulares.

Perímetro do polígono regular

Para calcular o perímetro de um polígono regular, basta multiplicar a medida do seu lado pela quantidade de lados que esse polígono possui. Já que ele é equilátero, o perímetro do polígono regular é calculado pela fórmula:

\(P=n⋅l\)

• n → número de lados do polígono

• l → comprimento do lado do polígono

Exemplo:

Qual é o perímetro de um pentágono regular que possui lados medindo 8 cm?

Resolução:

Calculando o perímetro, sabendo que o pentágono é regular, temos que:

\(P=5⋅8=40\ cm\)

Ângulos internos de um polígono regular

O polígono regular é equiângulo, ou seja, todos os ângulos internos possuem a mesma medida. Sendo assim, para calcular o valor de cada ângulo podemos utilizar a fórmula da soma dos ângulos internos e dividir pelo número de lados do polígono.

De modo geral, para calcular o valor da soma dos ângulos internos de um polígono, utilizamos a fórmula:

\(S_i=180⋅(n-2)\)

• \(S_i\) → soma dos ângulos internos do polígono

• n → número de lados do polígono

Sabemos que em um polígono regular todos os ângulos são congruentes. Sendo assim, a fórmula para calcular a medida de cada um dos ângulos de um polígono regular é:

\(a_i=\frac{180⋅(n-2)}{n}\)

• \(a_i\) → medida do ângulo interno do polígono

Exemplo:

Qual é a medida de cada lado de um octógono regular?

Resolução:

Substituindo n = 8 na fórmula, temos que:

\(a_i=\frac{180⋅(8-2)}{8}\)

\(a_i=\frac{180⋅6}{8}\)

\(a_i=\frac{1080}8\)

\(a_i=135°\)

Ângulos externos de um polígono regular

A soma dos ângulos externos de qualquer polígono é 360°. Para calcular a medida de cada ângulo externo de um polígono regular, basta dividir 360° pelo número de lados desse polígono.

\(a_e=\frac{360}n\)

Exemplo:

Qual é a medida do ângulo externo de um triângulo equilátero?

Resolução:

Substituindo n = 5 na fórmula:

\(a_e=\frac{360}3\)

\(a_e=120°\)

Apótema do polígono regular

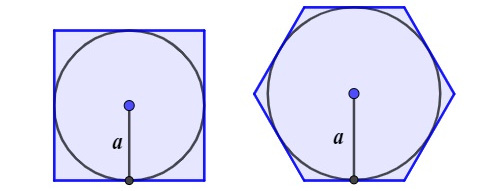
O apótema de um polígono regular é igual à medida do raio de uma circunferência circunscrita, sendo que o apótema é o comprimento do segmento que vai do centro do polígono até o lado, formando um ângulo de 90°.

Área do polígono regular

Para calcular a área de um polígono regular, além das fórmulas existentes específicas de cada polígono, há uma fórmula que podemos utilizar para todo polígono regular:

\(A=a⋅p\)

• a → apótema

• p → semiperímetro (metade do perímetro)

Exemplo:

Um pentágono possui lados medindo 4 cm e apótema igual a 2,75 cm. Qual o valor de sua área?

Resolução:

Sabemos que:

\(A=a⋅p\)

Calculando o perímetro:

P = \(4⋅5\)

P = 20

Então o semiperímetro é:

20 : 2 = 10

Logo, para calcular a área, temos que:

\(A=a⋅p\)

\(A=2,75⋅10\)

\(A=27,5\ cm^2\)

Diferença entre o polígono regular e o polígono irregular

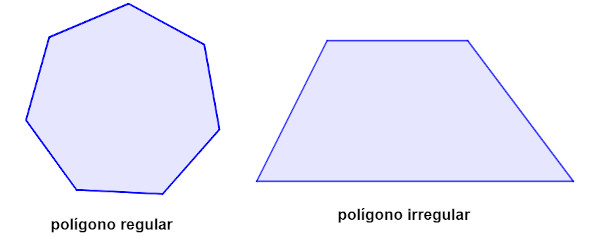
O polígono regular é um polígono que é equilátero e equiângulo ao mesmo tempo. Caso contrário, o polígono seria irregular. Então, o polígono irregular é o aquele que não possui todos os lados congruentes ou não possui todos os ângulos congruentes.

Como o polígono irregular possui pelo menos um dos lados com medida distinta, as propriedades para encontrar a medida de cada ângulo interno ou cada ângulo externo, por exemplo, não são válidas para o polígono regular.

Acesse também: Poliedros — as figuras tridimensionais formadas pela união de polígonos regulares

Exercícios sobre polígono regular

Um polígono que possui 12 lados é conhecido como dodecágono. Caso esse polígono seja regular, a medida de cada um dos seus ângulos internos é:

A) 100°

B) 125°

C) 150°

D) 175°

E) 200°

Resolução:

Alternativa C

Calculando a medida de cada ângulo interno, sabemos que n = 12:

\(a_i=\frac{180⋅(12-2)}{12}\)

\(a_i=\frac{180⋅10}{12}\)

\(a_i=\frac{1800}{12}\)

\(a_i=150°\)

Questão 2

O polígono é considerado regular se:

A) possuir lados paralelos congruentes entre si.

B) for um polígono equilátero.

C) for um polígono equiângulo.

D) for um polígono equilátero e equiângulo.

E) for um polígono com pelo menos um lado com medida diferente.

Resolução:

Alternativa D

O polígono é regular se ele é simultaneamente equilátero e equiângulo, ou seja, possuir lados congruentes entre si e ângulos congruentes entre si.

 

Por Raul Rodrigues de Oliveira
Professor de Matemática