Área do triângulo retângulo

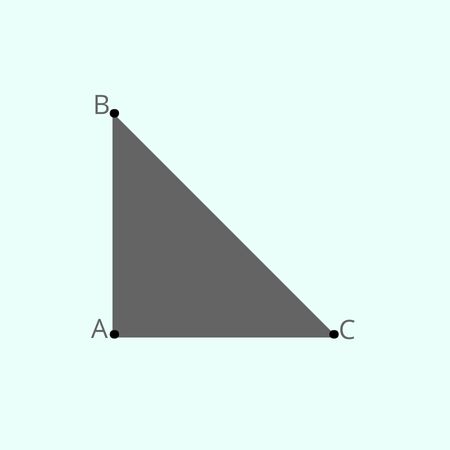
A área do triângulo retângulo é a medida de sua superfície. Essa área, assim como a de qualquer triângulo, corresponde à metade do produto entre a base e a altura. Como os catetos do triângulo retângulo formam 90°, é conveniente considerar um dos catetos como base, uma vez que o outro cateto será a altura.

Leia também: Área da pirâmide — como calcular?

Tópicos deste artigo

• 1 - Resumo sobre área do triângulo retângulo
• 2 - Qual a fórmula da área do triângulo retângulo?
• 3 - Como se calcula a área do triângulo retângulo?
• 4 - Exercícios resolvidos sobre área do triângulo retângulo

Resumo sobre área do triângulo retângulo

• O triângulo retângulo possui dois lados que formam 90° entre si (os catetos) e um terceiro lado, oposto ao ângulo de 90° (a hipotenusa).

• A área do triângulo retângulo é metade do produto entre a base e a altura.

• Se um dos catetos for a base do triângulo, a altura será o outro cateto.

• Se a base do triângulo for a hipotenusa, a altura será a distância entre a hipotenusa e o vértice oposto.

Qual a fórmula da área do triângulo retângulo?

A área de qualquer triângulo é dada pela metade do produto entre a base e a altura:

\(Área\ do\ triângulo =\frac{base\cdot altura}2\)

Considere ABC um triângulo retângulo com C =90°. Observe que podemos considerar o cateto BC como a base do triângulo. Consequentemente, o cateto AC será a altura desse triângulo. Essa estratégia é uma maneira de encontrar com facilidade a área de um triângulo retângulo, supondo que seus lados sejam conhecidos.

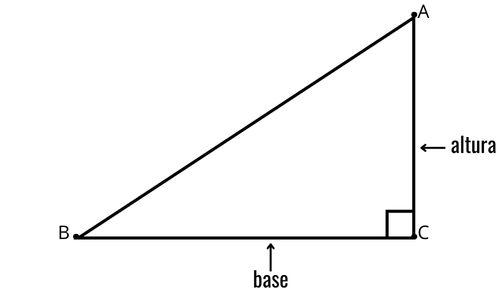
O mesmo raciocínio pode ser feito considerando o cateto AC como base, o que resulta no cateto BC como altura. A fórmula é aplicada da mesma maneira.

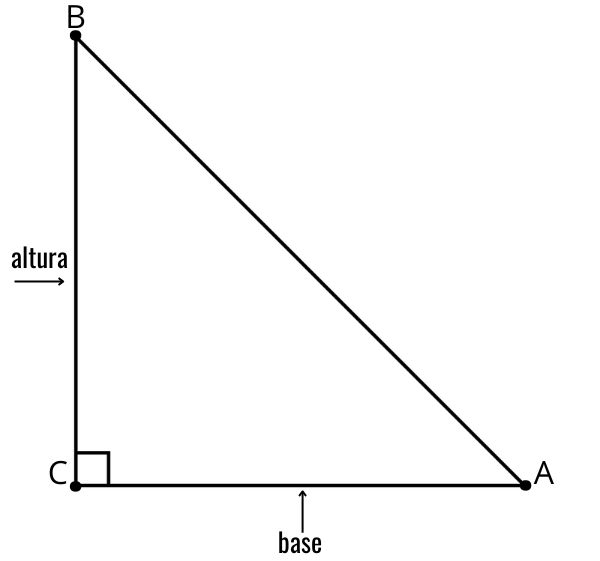
Também é possível tomar a hipotenusa AB como base do triângulo. Nesse caso, a altura do triângulo será o segmento com origem em \(\hat{C}\) que forma um ângulo reto com a base em um ponto D, sendo h a medida da altura CD.

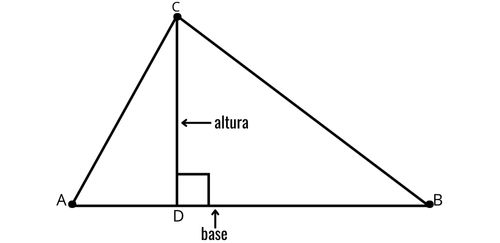
Nesse caso, a altura h pode ser determinada por meio da semelhança de triângulos entre ABC e um dos triângulos retângulos formados por CD. Considere a como a medida do lado BC, b como a medida do lado AC e c como a medida do lado AB. A semelhança de triângulos resulta na seguinte relação:

\(h=\frac{a ‧ b}c\)

Após obter o valor de h por essa expressão, basta aplicar a fórmula da área de um triângulo qualquer.

Como se calcula a área do triângulo retângulo?

Para calcular a área do triângulo retângulo, é necessário utilizar sua fórmula. Veja o exemplo a seguir.

• Exemplo:

Considere um triângulo retângulo com catetos medindo 6 cm e 8 cm. Determine a área desse triângulo.

Resolução:

Para simplificar, podemos tomar um dos catetos como base. Assim, o outro cateto será a altura.

Tomando o cateto de 6 cm como base e, portanto, o cateto de 8 cm como altura, temos

\(Área\ do\ triângulo = \frac{base ‧ altura}2=\frac{6 ‧ 8}2 = 24\ cm^2\)

Veja também: Área do trapézio — como calcular?

Exercícios resolvidos sobre área do triângulo retângulo

Questão 1

Sendo ABC um triângulo retângulo com catetos medindo x cm e (2x - 1) cm e hipotenusa de medida (x + 1) cm, qual a área desse triângulo?  

Resolução:

Utilizando um dos catetos como base (e, portanto, o outro como altura):

\(Área\ do\ triângulo=\frac{base ‧ altura}2=\frac{x ‧ (2x-1)}2=\frac{2x^2-x}2=x^2-\frac{x}2 cm^2\)

Questão 2

Considere um terreno em formato de triângulo retângulo. A frente desse terreno corresponde a um dos catetos e tem medida de 5 metros. Sabendo que a distância da frente até a extremidade dos fundos do terreno é de 12 metros, determine a área do terreno.

Resolução:

Um dos catetos (a frente) mede 5 metros. Note que a distância entre a frente e o ponto mais extremo dos fundos (12 metros) corresponde ao outro cateto e, portanto, indica a altura do triângulo retângulo. Logo:

\(Área\ do\ triângulo=\frac{base ‧ altura}2=\frac{5 ‧ 12}2=30\ m^2\)

Por Maria Luiza Alves Rizzo
Professora de Matemática