Hexágono é o polígono que possui 6 lados. Ele é regular quando possui todos os lados e ângulos internos congruentes entre si. É irregular quando não possui essas características. O primeiro caso é o mais amplamente estudado, pois quando o hexágono é regular, ele possui propriedades específicas e fórmulas que nos permitem calcular sua área, perímetro e apótema.
Leia também: O que é um losango?
Tópicos deste artigo
- 1 - Resumo sobre hexágono
- 2 - O que é hexágono?
- 3 - Elementos do hexágono
- 4 - Classificação dos hexágonos
- 5 - Propriedades do hexágono
- 6 - Hexágono inscrito em uma circunferência
- 7 - Hexágono circunscrito em uma circunferência
- 8 - Prisma de base hexagonal
- 9 - Pirâmide de base hexagonal
- 10 - Exercícios resolvidos sobre hexágono
Resumo sobre hexágono
-
O hexágono é um polígono de 6 lados.
-
Ele é regular quando possui todos os lados congruentes.
-
É irregular quando não possui todos os lados congruentes.
-
Em um hexágono regular, cada ângulo interno mede 120°.
-
A soma dos ângulos externos de um hexágono regular é sempre 360°.
-
Para calcular a área de um hexágono regular, utilizamos a fórmula:
Anuncie aqui
\(A=\frac{3L^2\sqrt3}{2}\)
-
O perímetro de um hexágono é a soma dos seus lados. Quando ele é regular, temos:
P = 6L
-
O apótema de um hexágono regular é calculado pela fórmula:
\(a=\frac{\sqrt3}{2}L\)
O que é hexágono?
Hexágono é qualquer polígono que possui 6 lados, consequentemente 6 vértices e 6 ângulos. Como se trata de um polígono, ele é uma figura plana fechada com lados que não se cruzam. O hexágono é uma forma recorrente na natureza, como nos favos de mel, em estruturas da química orgânica, nos cascos de certas tartarugas e em flocos de neve.
-
Videoaula sobre polígonos
Elementos do hexágono
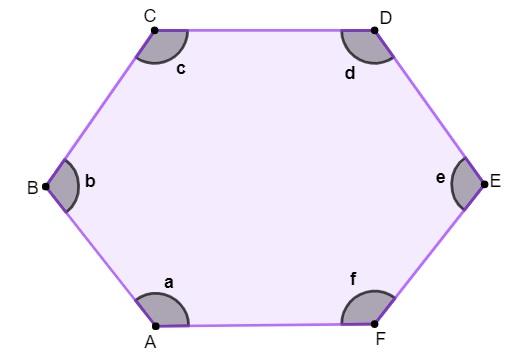
Um hexágono é composto por 6 lados, 6 vértices e 6 ângulos internos.
-
Vértices: os pontos A, B, C, D, E, F.
-
Lados: os segmentos \(\overline{AB},\overline{BC},\overline{CD},\overline{DE},\overline{EF},\ \overline{AF}\).
-
Ângulos internos: os ângulos a, b, c, d, f.
Classificação dos hexágonos
Os hexágonos, assim como os demais polígonos, podem ser classificados de duas formas.
-
Hexágono regular
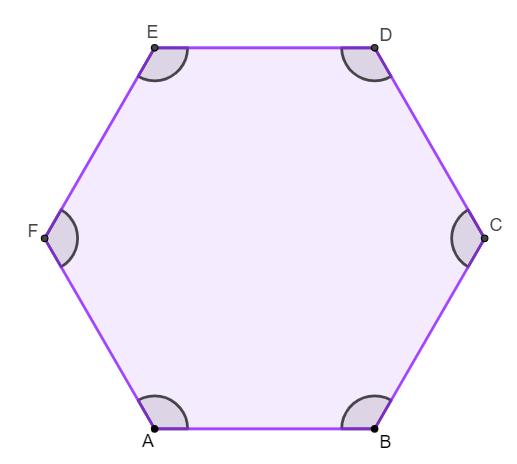
O hexágono é regular quando ele possui todos os seus lados congruentes — consequentemente, seus ângulos também serão congruentes. O hexágono regular é o mais importante dentre todos, sendo o mais amplamente estudando. É possível calcular vários de seus aspectos, como a área, com fórmulas específicas.
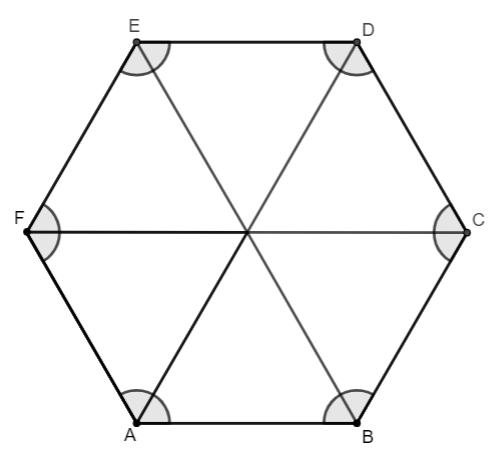
Observação: O hexágono regular pode ser dividido em 6 triângulos equiláteros, isto é, triângulos com todos os lados iguais.
→ Hexágono irregular
Hexágono irregular é aquele que possui lados com medidas diferentes. Ele pode ser convexo ou não convexo.
-
Hexágono irregular convexo
O hexágono é convexo quando possui todos os ângulos internos menores que 180°.
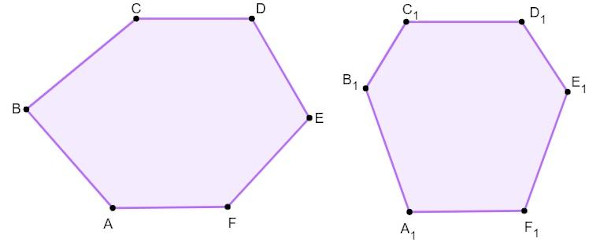
→ Hexágono irregular não convexo
O hexágono é não convexo quando possui ângulos internos maiores que 180°.
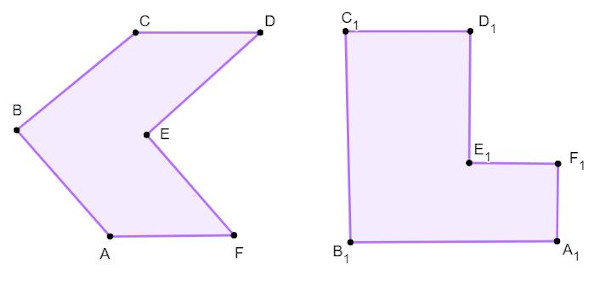
Propriedades do hexágono
→ Número de diagonais de um hexágono
A primeira propriedade importante é que em um hexágono convexo, há sempre 9 diagonais. Podemos encontrar essas 9 diagonais geometricamente:
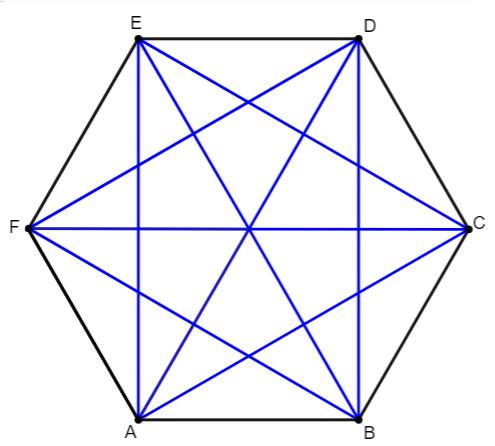
Também podemos encontrar as diagonais algebricamente, por meio da seguinte fórmula:
\(d=\frac{n\left(n-3\right)}{2}\)
Se substituirmos 6 na equação, temos que:
\(d=\frac{6\cdot\left(6-3\right)}{2}\)
\(d=\frac{6\cdot3}{2}\)
\(d=\frac{18}{2}\)
\(d=9\)
Então, um hexágono convexo sempre terá 9 diagonais.
Saiba mais: Diagonal do bloco retangular — segmento que liga dois de seus vértices que não estão na mesma face
→ Ângulos internos de um hexágono
Em um hexágono, a soma dos seus ângulos internos é igual a 720°. Para realizar essa soma, basta substituir 6 na fórmula:
\(S_i=180\left(n-2\right)\)
\(S_i=180\left(6-2\right)\)
\(S_i=180\cdot4\)
\(S_i=720\)
Em um hexágono regular, os ângulos internos sempre medirão 120° cada, pois
720° : 6 = 120°
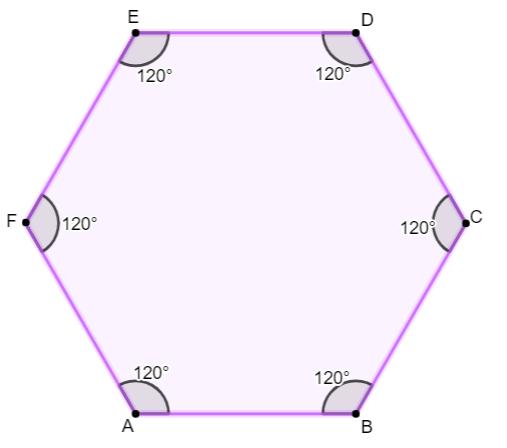
→ Ângulos externos de um hexágono regular
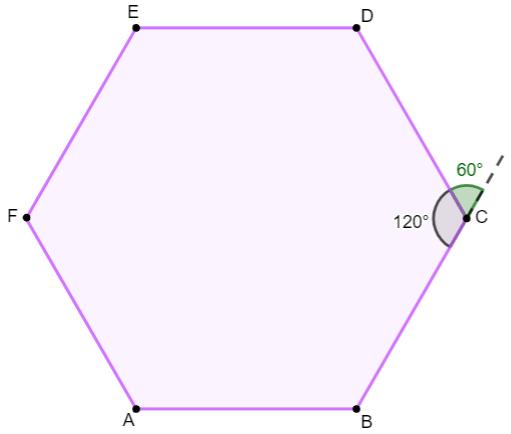
Quanto aos ângulos externos, sabemos que a soma deles é sempre igual a 360°. Como há 6 ângulos externos, cada um deles medirá 60°, pois
360° : 6 = 60°
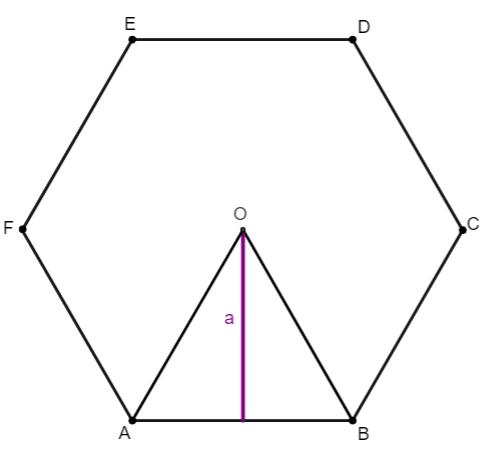
→ Apótema do hexágono regular
Considera-se apótema de um polígono regular o segmento de reta que liga o centro do polígono até o ponto médio do seu lado. Como sabemos, o hexágono regular é composto por 6 triângulos equiláteros, portanto, o apótema corresponde à altura de um desses triângulos equiláteros. O valor desse segmento pode ser calculado pela fórmula:
\(a=\frac{L\sqrt3}{2}\)
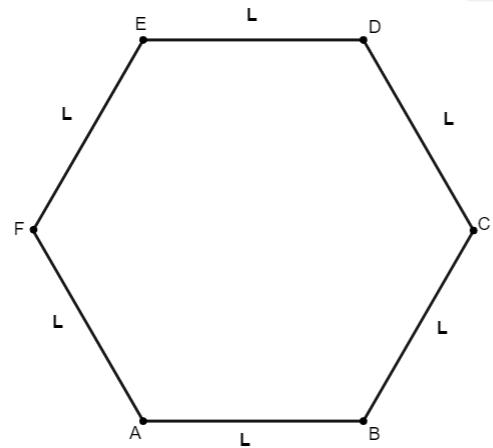
→ Perímetro do hexágono
Para calcular o perímetro de um hexágono, basta realizar a soma dos seus 6 lados. Quando o hexágono é regular, seus lados são congruentes, logo, é possível calcular o perímetro do hexágono por meio da fórmula:
P = 6L
→ Área do hexágono regular
Como sabemos que o hexágono regular é composto por 6 triângulos equiláteros de lado medindo L, é possível deduzir uma fórmula para o cálculo de sua área, utilizando o cálculo da área de um triângulo equilátero multiplicada por 6.
\(A=6\cdot\frac{L^2\sqrt3}{4}\)
Note que é possível fazer a simplificação dividindo por 2, gerando, então, a fórmula para o cálculo da área do hexágono:
\(A=3\cdot\frac{L^2\sqrt3}{2}\)
Hexágono inscrito em uma circunferência
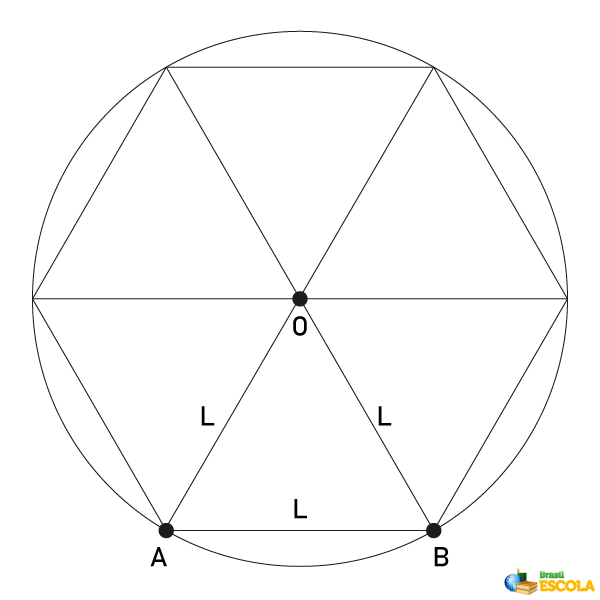
Dizemos que um polígono está inscrito em uma circunferência quando ele está dentro da circunferência, e os seus vértices são pontos desta. Podemos representar o hexágono regular inscrito em uma circunferência. Quando fazemos essa representação, é possível verificar que o comprimento do raio da circunferência é igual ao comprimento do lado do hexágono.
Saiba também: Círculo e circunferência — qual a diferença?
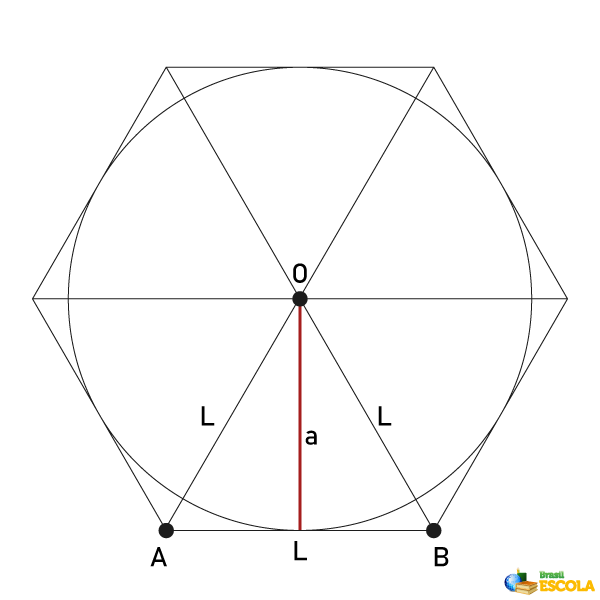
Hexágono circunscrito em uma circunferência
Dizemos que um polígono está circunscrito a uma circunferência quando a circunferência está dentro desse polígono. Podemos representar o hexágono regular circunscrito. Nesse caso, a circunferência é tangente ao ponto médio de cada um dos lados do hexágono, o que faz com que o raio da circunferência seja igual ao apótema do hexágono.
Prisma de base hexagonal
A Geometria Plana é a base para os estudos da Geometria Espacial. O hexágono pode estar presente na base de sólidos geométricos, como nos prismas.
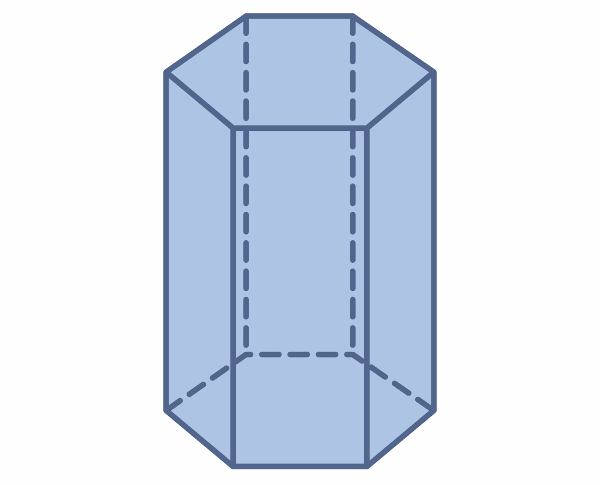
Para descobrir o volume de um prisma, calculamos o produto entre a área da base e a altura. Como a sua base é um hexágono, seu volume pode ser calculado por:
\(V=3\cdot\frac{L^2\sqrt3}{2}\cdot h\)
Leia também: Volume dos sólidos geométricos — como calcular?
Pirâmide de base hexagonal
Além do prisma de base hexagonal, existem também as pirâmides de base hexagonal.
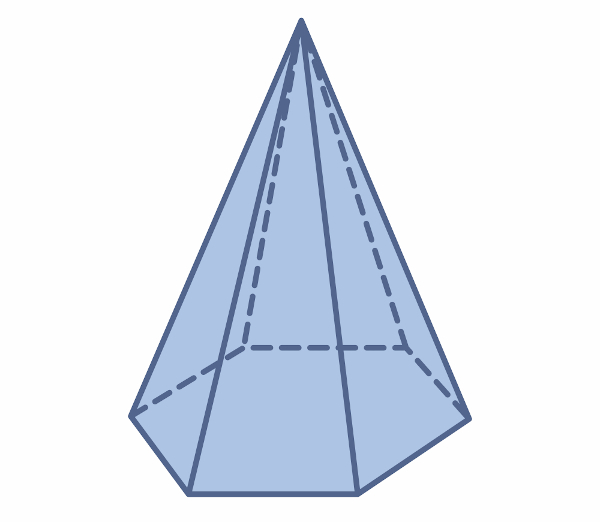
Para descobrir o volume de uma pirâmide de base hexagonal, calculamos o produto entre a área da base, a altura e dividimos por 3.
\(V=3\cdot\frac{L^2\sqrt3}{2}\cdot h:3\)
Note que multiplicamos e dividimos por três, o que possibilita uma simplificação. Então, o volume de uma pirâmide de base hexagonal é calculado pela fórmula:
\(V=\frac{L^2\sqrt3}{2}\cdot h\)
Exercícios resolvidos sobre hexágono
Questão 1
Um terreno possui formato de um hexágono regular. Deseja-se cercar essa área com arame farpado, de maneira que o arame dê 3 voltas em torno do território. Sabendo que foram gastos, ao todo, 810 metros de arame para cercar todo o terreno, a área desse hexágono mede, aproximadamente:
(Use \(\sqrt3=1,7\))
A) 5102 m²
B) 5164 m²
C) 5200 m²
D) 5225 m²
E) 6329 m²
Resolução:
Alternativa B
O perímetro do hexágono regular é
\(P=6L\)
Como foram dadas 3 voltas, para dar uma só volta foi gasto o total de 270 metros, pois sabemos que:
810 : 3 = 270
Então, temos:
\(6L=270\)
\(L=\frac{270}{6}\)
\(L=45\ metros\)
Conhecendo a medida do lado, calcularemos a área:
\(A=3\cdot\frac{L^2\sqrt3}{2}\)
\(A=3\cdot\frac{{45}^2\sqrt3}{2}\)
\(A=3\cdot\frac{2025\sqrt3}{2}\)
\(A=3\cdot1012,5\sqrt3\)
\(A=3037,5\sqrt3\)
\(A=3037,5\cdot1,7\)
\(A=5163,75m^2\)
Arredondando, obtemos:
\(A\approx5164m^2\)
Questão 2
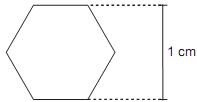
(PUC - RS) Para uma engrenagem mecânica, deseja-se fazer uma peça de formato hexagonal regular. A distância entre os lados paralelos é de 1 cm, conforme a figura abaixo. O lado desse hexágono mede ______ cm.
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt3}{3}\)
C) \(\sqrt3\)
D) \(\frac{\sqrt5}{5}\)
E) 1
Resolução:
Alternativa B
Em relação ao hexágono regular, sabemos que seu apótema é a medida do centro até o ponto médio de um dos lados. Assim, o apótema é a metade da distância indicada na imagem. Logo, temos que:
\(2a=1cm\)
\(a=\frac{1}{2}\)
O apótema é, então, igual a \(\frac{1}{2}\). Existe uma relação entre os lados do hexágono e o apótema, pois em um hexágono regular, temos:
\(a=\frac{L\sqrt3}{2}\)
Como conhecemos o valor do apótema, podemos substituir \(a=\frac{1}{2}\) na equação:
\(\frac{1}{2}=\frac{L\sqrt3}{2}\)
\(1=L\sqrt3\)
\(L\sqrt3=1\)
\(L=\frac{1}{\sqrt3}\)
Racionalizando a fração:
\(L=\frac{1}{\sqrt3}\cdot\frac{\sqrt3}{\sqrt3}\)
\(L=\frac{\sqrt3}{3}\)