O que é círculo?

Círculo é uma figura geométrica plana composta por todos os pontos a uma distância igual ou menor que r de determinado centro P. Muitos objetos têm o formato de círculo: relógios, espelhos, pratos, botões, chaveiros, adesivos, etc.

Leia também: O que é um polígono?

Tópicos deste artigo

• 1 - Resumo sobre círculo
• 2 - Círculo e circunferência
  • â? Diferença entre círculo e circunferência
  • → Videoaula sobre círculo e circunferência
• 3 - Elementos do círculo
• 4 - Fórmulas do círculo
  • Fórmula do perímetro do círculo
  • Fórmula da área do círculo
• 5 - Exercícios resolvidos sobre círculo

Resumo sobre círculo

• O círculo de centro P e raio r é o conjunto de pontos no plano que estão a uma distância igual ou menor que r de P.

• A circunferência de centro P e raio r é o conjunto de pontos no plano que estão a uma distância igual a r de P.

• O círculo é a região interna da circunferência.

• Centro e raio são os elementos fundamentais do círculo.

• O perímetro de um círculo de raio r é o comprimento da circunferência de raio r, cuja fórmula é

\(C = 2\pi r\)

• A fórmula da área de um círculo de raio r é

\(A=\pi r^2\)

Círculo e circunferência

Dado um ponto P e um número real positivo r, a circunferência de centro P e raio r é o conjunto de pontos no plano que está exatamente a uma distância r de P. Na imagem abaixo, a circunferência é a curva em verde.

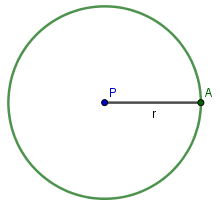
Círculo e circunferência não são a mesma figura geométrica. Vejamos a seguir o que isso significa.

➝ Diferença entre círculo e circunferência

O círculo e a circunferência estão relacionados, mas são figuras diferentes. Considere um ponto P e um raio de medida r. A circunferência é formada por todos os pontos cuja distância ao ponto P seja igual a r. Formalmente, escrevemos que, se A pertence à circunferência, então

\(d(A,P) = r\)

Já o círculo é formado por todos os pontos cuja distância ao ponto P seja igual ou menor que r. Formalmente, escrevemos que, se A pertence ao círculo, então

\(d(A,P)\le r\)

Em resumo: a circunferência é o contorno, a borda, o limite do círculo. Na imagem abaixo, temos uma circunferência (à esquerda) e um círculo (à direita) de mesmo raio. O círculo é a região interna da circunferência.

→ Videoaula sobre círculo e circunferência

Elementos do círculo

Os elementos mais importantes do círculo são o centro e o raio. O centro, como o nome sugere, é o ponto central do círculo. Já o raio é a distância entre o centro do círculo e sua borda.

Ao escrever sobre um círculo (ou circunferência), normalmente indicamos o centro e o raio entre parênteses e separados por vírgula. Assim, um círculo c de centro P e raio r é representado por

\(c\ (P,r)\)

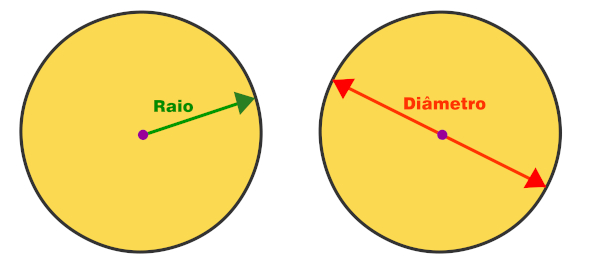
Outro elemento do círculo é o diâmetro, que corresponde ao segmento que cruza o centro do círculo e tem extremidades em dois pontos do círculo. Assim, a medida do diâmetro é o dobro da medida do raio.

Fórmulas do círculo

• Fórmula do perímetro do círculo

O perímetro do círculo corresponde ao comprimento da circunferência de mesmo raio. A medida do comprimento C de uma circunferência de raio r é dada por

\(C = 2\pi r\)

Exemplo:

Qual o perímetro aproximado de um círculo com 3 cm de raio? (Utilize π=3,14).

\(C = 2\cdot 3,14\cdot 3\)

\(C = 18,84\ cm\)

Curiosidade: o número irracional π é a razão entre o comprimento de uma circunferência e seu raio.

• Fórmula da área do círculo

A área do círculo é a medida de sua região interior. Em um círculo de raio r, sua área A é dada por

\(A=\pi r^2\)

Exemplo:

Qual a área de um círculo com 7 cm de raio? (Utilize π = 3,1).

\(A=3,1\cdot 7^2\)

\(A = 3,1\cdot 49\)

\(A=151,9\ cm^2\)

Saiba mais: Como calcular o perímetro de um polígono?

Exercícios resolvidos sobre círculo

Questão 1

A razão entre o perímetro e a área de um círculo com 5 de raio é

a) 0,4

b) 1,0

c) 1,5

d) 2,5

e) 3,4

Resolução

O perímetro do círculo (comprimento da circunferência correspondente) é

\(C = 2\pi \cdot 5 = 10\pi \)

A área do círculo é

\(A=\pi \cdot 5^2=25\pi \)

Logo,

\(\frac{C}A=\frac{10\pi }{25\pi}=0,4\)

Alternativa A.

Questão 2

Se a área de círculo é 196π, a medida d do diâmetro é

a) 12

b) 14

c) 28

d) 49

e) 98

Resolução

\(A=\pi \cdot r^2\)

\(196\pi =\pi \cdot r^2\)

\(196=r^2\)

\(r=\sqrt{196}=14\)

Como a medida do diâmetro é o dobro da medida do raio, tem-se que d = 28.

Alternativa C.

Fontes

LIMA, E. L. Geometria Analítica e Álgebra Linear. Rio de Janeiro: IMPA, 2014.

REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.

Por Maria Luiza Alves Rizzo
Professora de Matemática