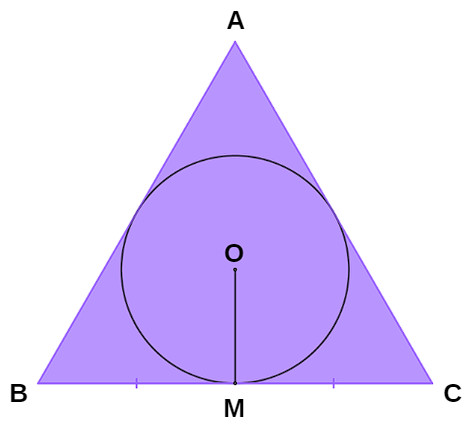
O apótema de um polígono é um segmento com extremidades no centro do polígono e no ponto médio de um dos lados. Esse segmento forma um ângulo de 90° com o respectivo lado do polígono.
Para calcular a medida do apótema, é necessário considerar as características do polígono em questão. Dependendo da forma geométrica, é possível construir uma fórmula para obter essa medida. Uma observação importante é que a medida do apótema de um polígono regular é igual à medida do raio da circunferência inscrita no polígono.
Leia também: O que é a bissetriz?
Tópicos deste artigo
- 1 - Resumo sobre o apótema
- 2 - Exemplos de apótema
- 3 - Quais as fórmulas do apótema?
- 4 - Como se calcula o apótema?
- 5 - Exercícios resolvidos sobre o apótema
Resumo sobre o apótema
-
O apótema é o segmento de um polígono que liga o centro (ponto de encontro das mediatrizes) ao ponto médio de um dos lados.
-
O ângulo entre o apótema e o respectivo lado do polígono mede 90°.
-
A medida do apótema de um polígono regular é igual à medida do raio da circunferência inscrita no polígono.
-
O apótema OM de um triângulo equilátero de lado l é dado pela fórmula
\(OM = \frac{l\sqrt3}6\)
-
O apótema OM de um quadrado de lado l é dado pela fórmula
\(OM = \frac{l}2\)
-
O apótema OM de um hexágono regular de lado l é dado pela fórmula
\(OM = \frac{l\sqrt3}2\)
-
O apótema de uma pirâmide é o segmento que une o vértice ao ponto médio de uma das arestas da base, e sua medida pode ser obtida pelo teorema de Pitágoras.
Exemplos de apótema
Para encontrar o apótema de um polígono, devemos construir o segmento de reta que une o centro do polígono com o ponto médio de um dos lados. Lembre-se de que o centro de um polígono é o ponto de encontro das mediatrizes.
Nesses exemplos, o apótema foi considerado em polígonos no plano. Entretanto, existe um objeto espacial que possui um tipo diferente de apótema: a pirâmide.
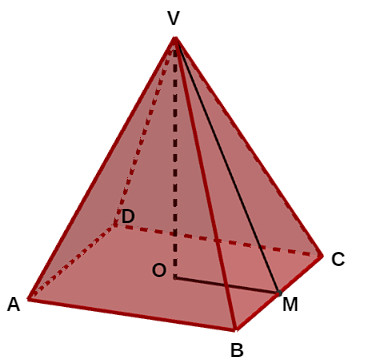
Em uma pirâmide, há dois tipos de apótema: o apótema da base, que é o apótema do polígono que forma a base da pirâmide, e o apótema da pirâmide, que é o segmento que une o vértice ao ponto médio de uma aresta da base (ou seja, é a altura de uma face lateral da pirâmide).
No exemplo de base quadrada abaixo, o segmento OM é o apótema da base e o segmento VM é o apótema da pirâmide, sendo M o ponto médio de BC.
Quais as fórmulas do apótema?
Conhecendo as características de um polígono, em especial dos polígonos regulares, podemos desenvolver fórmulas para o cálculo da medida do apótema. Vejamos quais são essas fórmulas para os principais polígonos regulares.
-
Fórmula do apótema do triângulo equilátero
No caso do triângulo equilátero, a altura e a mediana relativas a um determinado lado são coincidentes. Isso significa que o centro do polígono coincide com o baricentro do triângulo. Assim, o ponto O divide a altura AM da seguinte forma:
\(AO = \frac{2}3 AM\) e \(OM=\frac{1}3 AM\)
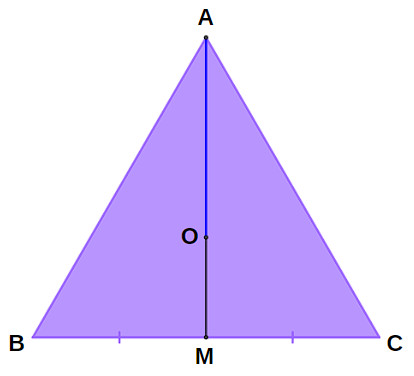
Lembre-se de que a medida da altura de um triângulo equilátero de lado l é dada por:
\(Altura\ triângulo\ equilátero=\frac{l\sqrt3}2\)
Portanto, como a AM é altura do triângulo equilátero ABC e o segmento OM é o apótema do triângulo, podemos elaborar a seguinte expressão para a medida de OM, considerando que o lado do triângulo mede l:
\(OM =\frac{1}3 AM = \frac{1}3 ⋅\frac{l\sqrt3}2\)
\(OM = \frac{l\sqrt3}6\)
-
Fórmula do apótema do quadrado
No caso do quadrado, a medida do apótema corresponde à metade do comprimento do lado. Assim, se O é o centro do quadrado, M é o ponto médio de um dos lados e l é a medida do lado do quadrado, então a fórmula do apótema OM é
\(OM=\frac{l}2\)
-
Fórmula do apótema do hexágono regular
No hexágono regular, o apótema corresponde à altura de um triângulo equilátero com vértices em duas extremidades de um dos lados e no centro do polígono. No exemplo abaixo, o apótema OM do hexágono regular é a altura do triângulo equilátero OCD, em que M é o ponto médio de CD.
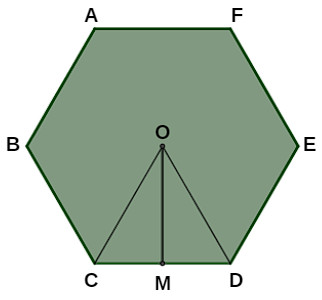
Como comentamos antes, a altura de um triângulo equilátero é conhecida. Assim, se o lado do hexágono regular mede l, então a fórmula do apótema OM é
\(OM =\frac{l\sqrt3}2\)
-
Fórmula do apótema da pirâmide
A medida do apótema da pirâmide pode ser obtida com o auxílio do teorema de Pitágoras. No exemplo abaixo, em uma pirâmide quadrada, o triângulo VOM é retângulo, com catetos VO e OM e hipotenusa VM. Perceba que VO é a altura da pirâmide, OM é o apótema da base e VM é o apótema da pirâmide.
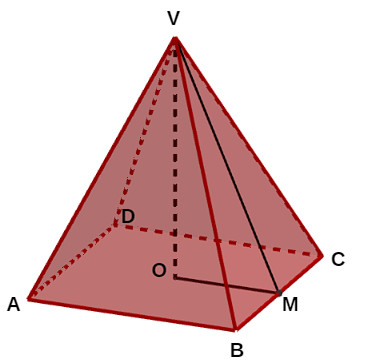
Assim, para determinar a medida do apótema da pirâmide, devemos aplicar o teorema de Pitágoras:
\((VM)^2=(VO)^2+(OM)^2\)
Cuidado! VM é a altura de um triângulo isósceles, não de um triângulo equilátero. Assim, nesse caso, não podemos utilizar a fórmula da altura de um triângulo equilátero.
Como se calcula o apótema?
Para calcular o apótema de um polígono ou da pirâmide, podemos utilizar as fórmulas construídas ou associar o apótema ao raio da circunferência inscrita.
-
Exemplo 1: Considere que uma circunferência de raio 3 cm está inscrita em um triângulo equilátero. Qual a medida do apótema desse triângulo?
Como o apótema de um polígono possui a mesma medida que o raio da circunferência inscrita, o apótema do triângulo mede 3 cm.
-
Exemplo 2: Qual a medida do apótema de um hexágono regular com 4 cm de lado?
Anuncie aqui
Utilizando a fórmula para o apótema de um hexágono regular com \(l=4 \) cm, temos que
\(Medida\ do\ apótema=\frac{4\sqrt3}2=2\sqrt3\ cm\)
Leia também: Tudo sobre os pontos notáveis de um triângulo
Exercícios resolvidos sobre o apótema
Questão 1
Se uma pirâmide com 4 cm de altura possui um apótema da base com 3 cm, então a medida do apótema da pirâmide é
a) 5 cm
b) 6 cm
c) 7 cm
d) 8 cm
e) 9 cm
Resolução:
Em uma pirâmide, podemos construir um triângulo retângulo em que um cateto é o apótema da base, o outro cateto é a altura da pirâmide e a hipotenusa é o apótema da pirâmide. Assim, aplicando o teorema de Pitágoras para hipotenusa de medida x,
\(x^2=3^2+4^2\)
\(x = 5\ cm\)
Alternativa A.
Questão 2
Se o apótema de um quadrado mede y cm, então o lado do quadrado mede
a) \(\frac{1}3y \) cm
b) \(\frac{1}2y \) cm
c) y cm
d) 2y cm
e) 3y cm
Resolução
O apótema de um quadrado possui metade da medida do lado do quadrado. Portanto, se o apótema mede y cm, o quadrado mede 2y cm.
Alternativa D.
Por Maria Luiza Alves Rizzo
Professora de Matemática