Simetria

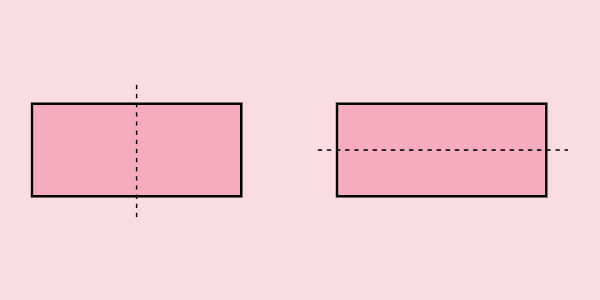
A simetria é tudo aquilo que pode ser divido em partes, de forma que as partes coincidam perfeitamente quando sobrepostas. Trata-se de um importante conceito estudado na geometria. Podemos perceber a presença da simetria na arte, na geometria, na biologia e em outras áreas do conhecimento.

Existem diferentes tipos de simetria: a reflexiva, a de translação, e a rotacional. Simetria e assimetria são conceitos contrários, ou seja, ou uma figura é simétrica ou é assimétrica. Para verificar se uma figura é simétrica ou assimétrica, traçamos uma reta, dividindo-a. Caso ela seja formada de duas formas que se coincidam perfeitamente quando sobrepostas, então essa figura é simétrica, e a reta é conhecida como eixo de simetria; caso contrário, a figura será assimétrica.

Leia também: Planificação de sólidos geométricos

Tópicos deste artigo

• 1 - Resumo sobre simetria
• 2 - O que é simetria?
• 3 - Quais são os tipos de simetria?
  • Simetria reflexiva
  • Simetria de translação
  • Simetria de rotação
• 4 - Diferença entre simetria e assimetria
• 5 - Importância da simetria

Resumo sobre simetria

• Uma forma é conhecida como simétrica se, ao ser dividida em partes, estas se coincidam perfeitamente quando sobrepostas.
• Uma figura pode ser simétrica ou assimétrica.
  • A figura simétrica pode transladar ou rotacionar sem alterar a figura.
  • A figura assimétrica é oposta, sua rotação ou translação altera a figura.  
• Existem três tipos de simetria, são elas:
  • Simetria reflexiva: quando a forma pode ser dividida em duas partes iguais.
  • Simetria de translação: quando uma figura é movida sem rotacionar, em qualquer direção.
  • Simetria de rotacional: quando uma figura é rotacionada em relação a um de seus pontos.

O que é simetria?

A simetria é um dos primeiros conceitos estudados na geometria. Ela está ligada à harmonia da forma, ao belo; a simetria é tudo aquilo que podemos dividir em partes, de forma que as partes coincidam perfeitamente quando sobrepostas, o que quer dizer que, ao dividirmos essa forma, encontraremos duas formas idênticas.

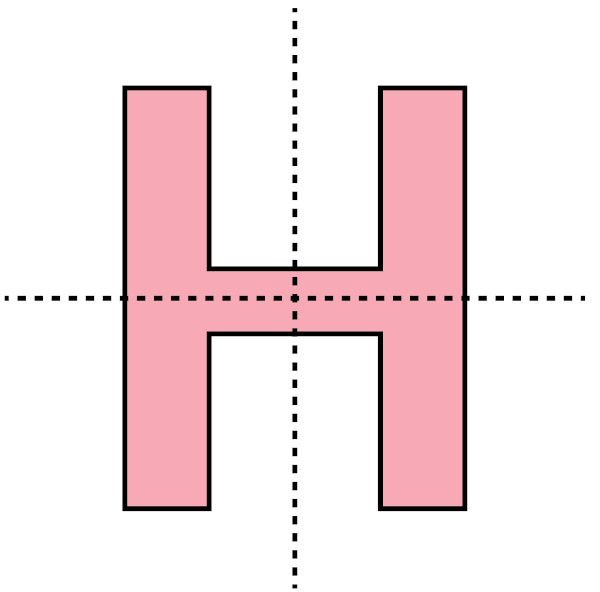
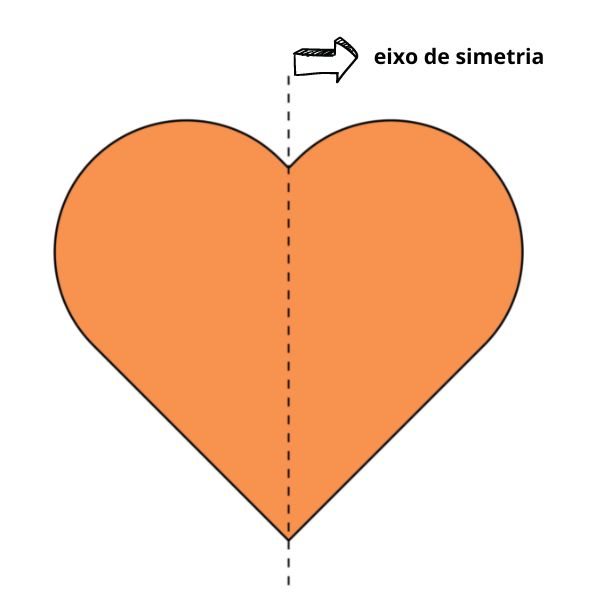
Podemos perceber a presença da simetria na geometria, na arte, na arquitetura, na natureza, entre outros lugares do nosso cotidiano. O eixo de simetria de uma figura é uma reta que passa pelo centro da figura, dividindo-a em partes simétricas.

Quais são os tipos de simetria?

Existem três tipos de simetria, a reflexiva, a de translação e a rotacional.

• Simetria reflexiva

Como o nome sugere, está ligada ao reflexo; é quando uma imagem é o reflexo da outra.

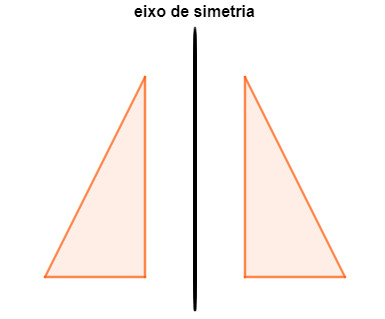
É importante perceber que, na reflexão, o triângulo muda a oposição dos lados, pois, nesse caso, é como se o primeiro triângulo estivesse sendo refletido em um espelho pelo segundo triângulo.

Podemos verificar essa simetria na natureza, em paisagens com água por exemplo:

A simetria de reflexão também pode ser conhecida como simetria do espelho ou simetria axial, nesse caso, é como se o eixo fizesse o mesmo que o espelho.

• Simetria de translação

Conhecemos como translação quando há um deslocamento da figura. Nesse caso, a figura só se deslocará para frente, para trás, para os lados, de forma que não pode rotacionar.

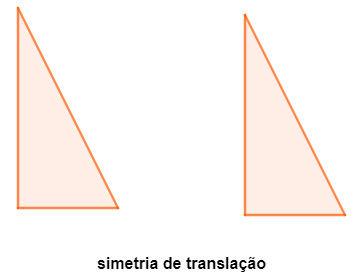
É importante ressaltar que, na translação, as figuras possuem mesma área, logo, não pode ocorrer aumento de área, mudanças em sua forma, ou mesmo uma rotação, pois a rotação da figura é um outro caso de simetria.

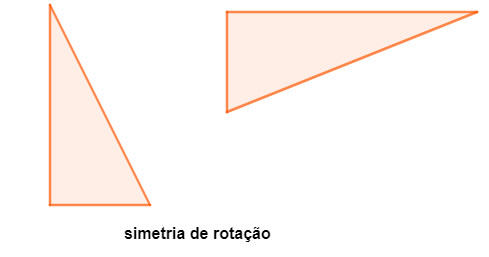
• Simetria de rotação

É a transformação geométrica em que a figura é obtida após girar-se a figura principal. A rotação pode ser feita no sentido horário ou no anti-horário.

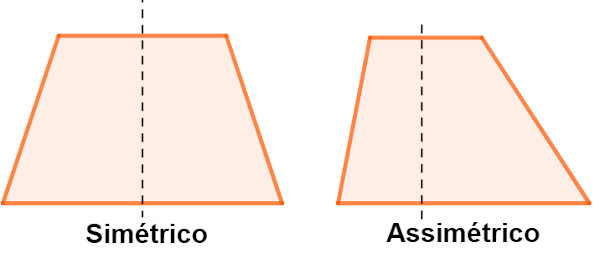
Diferença entre simetria e assimetria

Como vimos, a simetria é quando temos duas figuras que se sobrepõem perfeitamente; já uma assimetria é o caso contrário, ou seja, quando não há padrão ou semelhança entre as partes da figura. Então podemos dizer que os conceitos de simetria e assimetria são contrários, ou temos simetria ou temos assimetria. Cada um dos casos possui função importante no estudo da geometria.

Importância da simetria

O estudo da simetria está presente em várias áreas de conhecimento, como na biologia, mais especificamente no estudo da simetria corporal dos seres vivos e na natureza. Essa é uma área importante de estudo da biologia, pois é com base nela que surgem algumas classificações zoológicas.

Podemos perceber também a importância da simetria na arte e na arquitetura. A simetria está ligada ao belo e ao harmônico, por isso ela está presente em várias obras de arte e construções.

Por Raul Rodrigues de Oliveira
Professor de Matemática