Ao comparar figuras geométricas existem algumas conclusões possíveis: As figuras são congruentes, ou seja, seus lados e ângulos possuem as medidas iguais; as figuras são diferentes ou as figuras são semelhantes, isto é, possuem ângulos correspondentes com medidas iguais e lados correspondentes com medidas proporcionais.
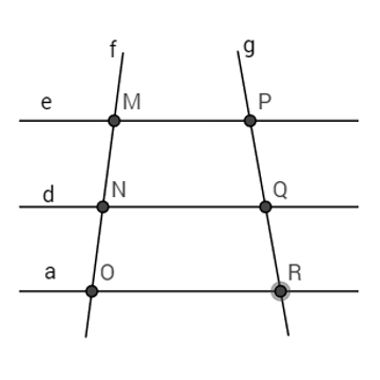
Um matemático chamado Tales de Mileto observou que existe proporcionalidade entre os segmentos de reta formados por um feixe de retas paralelas cortadas por retas transversais. Observe a imagem seguinte:
A proporcionalidade válida observada por Tales é a das igualdades:
MN = PQ = NO
MO PR QR
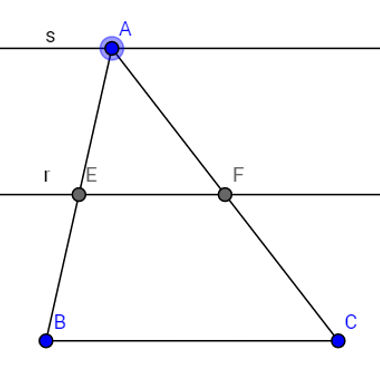
Essa importante descoberta logo foi observada nos triângulos. Quando um triângulo ABC é intersectado em dois de seus lados, AB e AC, por uma reta r e essa reta é paralela ao lado restante, BC, do triângulo, então valem essas mesmas proporcionalidades, uma vez que o vértice A desse triângulo pode ser visto como ponto pertencente a uma reta também paralela a r. Observe:
Nesse triângulo, valem as seguintes proporcionalidades:
AE = AF = EB
AB AC FC
Uma vez observadas essas proporcionalidades, e considerando os triângulos AEF e ABC como triângulos distintos, basta observar que o ângulo interno do vértice A é comum aos dois triângulos para afirmar que eles são semelhantes, pelo caso de semelhança Lado – ângulo – lado (LAL). Mais especificamente:
-
O Ângulo interno do vértice A é comum aos dois triângulos, por isso é igual na comparação entre os dois.
-
Os lados AE e AF pertencentes ao triângulo AEF são proporcionais aos lados AC e AB pertencentes ao triângulo ABC.
Portanto, pelo caso LAL de semelhança de triângulos, os triângulos são semelhantes.
Em resumo, tendo um triângulo qualquer como base, pode-se chegar à seguinte propriedade: Em um triângulo ABC, uma reta r intersecta os lados AB e AC nos pontos E e F de forma que a reta r é paralela ao lado BC, Então os triângulos ABC e AEF são semelhantes.
Essa propriedade ficou conhecida como o teorema fundamental da semelhança.
Por Luiz Paulo Moreira
Graduado em Matemática