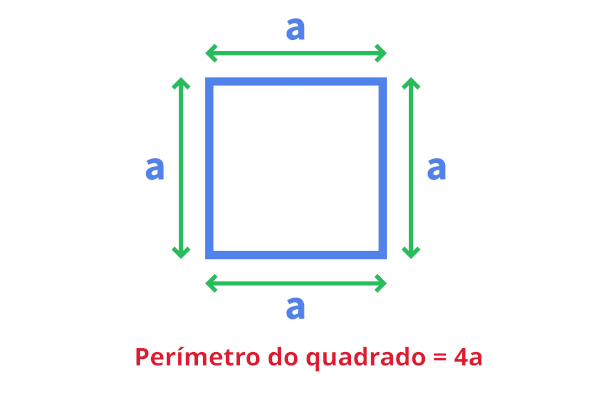
O perímetro do quadrado é a medida do contorno dessa figura geométrica. Lembre-se de que o quadrado é um polígono formado por quatro lados de mesma medida. Isso significa que seu perímetro será a soma entre quatro lados congruentes.
Considere a a medida do lado de um quadrado. Assim, o perímetro desse quadrado será \(a+a+a+a = 4a\).
Leia também: O que são quadriláteros?
Tópicos deste artigo
- 1 - Resumo sobre perímetro do quadrado
- 2 - Como calcular o perímetro do quadrado?
- 3 - Perímetro do quadrado com lados desconhecidos
- 4 - Como calcular o perímetro do quadrado inscrito em uma circunferência?
- 5 - Como calcular a área do quadrado?
- 6 - Exercícios resolvidos sobre perímetro do quadrado
Resumo sobre perímetro do quadrado
-
O quadrado é um polígono com quatro lados congruentes e quatro ângulos retos.
-
O perímetro de um quadrado é a soma dos quatro lados.
-
Se o lado do quadrado mede a, o perímetro é dado por
\(P_{quadrado} =a+a+a+a=4a\)
-
A diagonal de um quadrado de lado a é dada por
Anuncie aqui
\(d_{quadrado} =a\sqrt2\)
-
A área de um quadrado de lado a é dada por
\(A_{quadrado} =a⋅a=a^2\)
Como calcular o perímetro do quadrado?
Para calcular o perímetro do quadrado, basta conhecer a medida de seu lado a e substituir na soma dos lados da figura.
-
Exemplo:
Qual o perímetro de um quadrado com 3 cm de lado?
\(P_{quadrado} =3+3+3+3 = 4 ⋅3 = 12\ cm\)
Perímetro do quadrado com lados desconhecidos
Mas e se o lado do quadrado for desconhecido, ou seja, se o valor de a não estiver expresso? Nesse caso, é necessário utilizar outras informações sobre o quadrado para determinar primeiro a medida do lado e depois calcular o perímetro.
Vejamos um exemplo de como calcular o perímetro do quadrado a partir da medida da diagonal. Lembre-se de que a diagonal do quadrado é o segmento com extremidades em vértices não consecutivos.
-
Exemplo:
Determine o perímetro de um quadrado cuja diagonal mede 52 cm.
A diagonal de um quadrado de lado a é obtida pela expressão
\(d_{quadrado} =a\sqrt2\)
Portanto,
\(5\sqrt2 \ cm=a\sqrt2\)
\(a = 5\ cm\)
Logo, o perímetro desse quadrado é
\(P_{quadrado} = 4⋅5 = 20\ cm\)
Veja também: Polígonos inscritos em circunferências
Como calcular o perímetro do quadrado inscrito em uma circunferência?
Se um quadrado está inscrito em uma circunferência, então os quatro vértices do quadrado pertencem à circunferência. Observe a imagem abaixo, em que um quadrado de lado a está inscrito em uma circunferência de raio R.
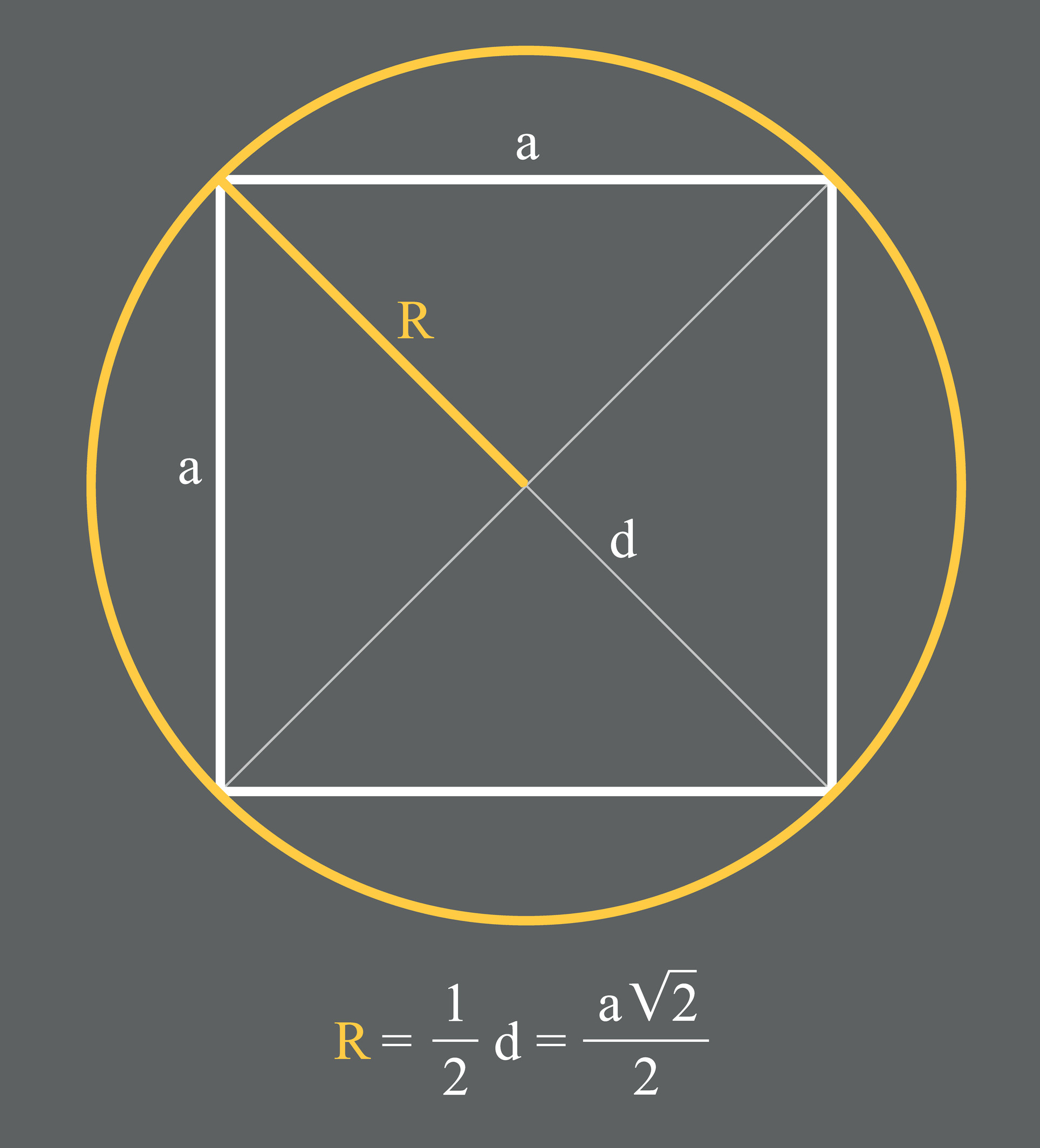
Note que o raio R da circunferência corresponde à metade da diagonal do quadrado. Ou seja,
\(R=\frac{d}2\)
Como \(d_{quadrado} =a\sqrt2\), temos que
\(R=\frac{a\sqrt2}2\)
Assim, dado um quadrado inscrito em uma circunferência de raio R, podemos utilizar essa expressão para determinar o lado a. A partir disso, podemos calcular o perímetro do quadrado.
-
Exemplo:
Qual o perímetro de um quadrado inscrito em uma circunferência de raio \(R=4\sqrt2\ cm\)?
\(R=\frac{a\sqrt2}2\)
\(4\sqrt2=\frac{a\sqrt2}2\)
\(8\sqrt2=a\sqrt2\)
\(a=8\ cm\)
Portanto,
\(P_{quadrado} = 4⋅8 = 32\ cm\)
Como calcular a área do quadrado?
A área de um quadrado é a região que esse polígono ocupa no plano. Para calcular essa medida, basta multiplicar os comprimentos dos lados adjacentes:
\(A_{quadrado} =a⋅a=a^2\)
-
Exemplo:
Anuncie aqui
Qual a área de um quadrado com 7 cm de lado?
\(A_{quadrado} =a^2\)
\(A_{quadrado} =7^2=49\ cm^2\)
Saiba mais: Fórmulas para calcular a área de figuras planas
Exercícios resolvidos sobre perímetro do quadrado
Questão 1
Se a área de um quadrado é 81 cm², o perímetro é igual a
a) 9 cm
b) 18 cm
c) 27 cm
d) 36 cm
e) 45 cm
Resolução
\(A_{quadrado} =a^2\)
\(81=a^2\)
\(a=\sqrt{81}=9\ cm\)
Portanto,
\(P_{quadrado} = 4⋅9 = 36\ cm\)
Alternativa D.
Questão 2
Considere um quadrado inscrito em uma circunferência cujo diâmetro mede \(10\sqrt2\). O perímetro do quadrado, em cm, é igual a
a) 10
b) 12
c) 22
d) 30
e) 40
Resolução
O diâmetro de uma circunferência é o dobro do raio. Assim, o diâmetro corresponde à medida da diagonal do quadrado inscrito:
\(d_{quadrado} =10\sqrt2\)
\(a\sqrt2=10\sqrt2\)
\(a=10\ cm\)
Logo,
\(P_{quadrado} = 4⋅10 = 40\ cm\)
Alternativa E.
Fontes
LIMA, E. L. Geometria Analítica e Álgebra Linear. Rio de Janeiro: IMPA, 2014.
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.
Por Maria Luiza Alves Rizzo
Professora de Matemática