Os estudos referentes a ângulos na circunferência auxiliaram e auxiliam até hoje a geometria plana. Com aplicações na astronomia e em outras áreas do conhecimento, esse estudo foi se aprofundando e desenvolvendo relações e propriedades diferentes para cada um dos casos. Os casos são:
-
ângulo central;
-
ângulo inscrito;
-
ângulo interno;
-
ângulo excêntrico interno;
-
ângulo excêntrico externo;
-
ângulo de segmento.
Para cada um dos casos, existem propriedades específicas que relacionam o arco da circunferência com o ângulo.
Leia também: Quais as diferenças entre círculo e circunferência?
Tópicos deste artigo
Elementos da circunferência
A circunferência possui elementos importantes para a compreensão dessa forma geométrica. Conhecemos como circunferência o conjunto de pontos que estão equidistantes do ponto C, conhecido como centro.
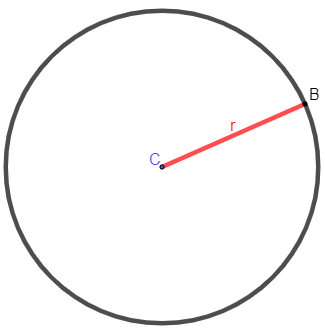
C → centro
r → raio
Além do centro e do raio, a circunferência possui também como elemento importante a corda, que são os segmentos que ligam uma extremidade à outra da circunferência.
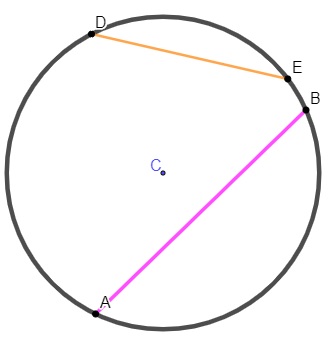
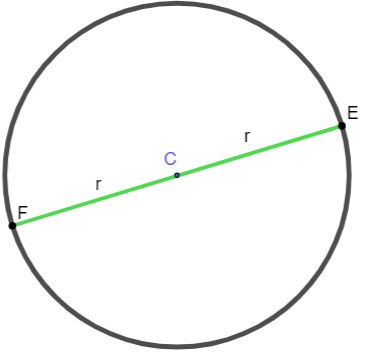
Quando essa corda passa pelo centro, ela é conhecida como diâmetro. O diâmetro de uma circunferência possui comprimento igual ao comprimento de dois raios e é um caso especial de corda.
Casos de ângulos na circunferência
Os estudos dos ângulos na circunferência relacionam os arcos formados pelos ângulos com o próprio ângulo.
-
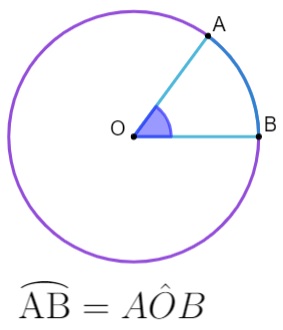
Ângulo central
Ocorre quando o ângulo está no centro da circunferência. Quando isso acontece, podemos dizer que a amplitude do ângulo central é igual à amplitude do arco.
Exemplo:
Calcule o valor do arco d.
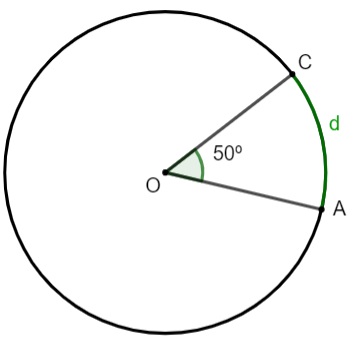
Como o ângulo central é igual a 50º, a amplitude do arco denotado por d também possui 50º.
Veja também: Como encontrar o centro de uma circunferência?
-
Ângulo inscrito na circunferência
Um ângulo é conhecido como inscrito quando o seu vértice for um ponto da circunferência. Quando isso ocorre, a amplitude do arco é igual à metade da medida do ângulo.
Exemplo:
Calcule o valor de α na imagem.
O arco é igual ao dobro do ângulo, ou seja, para encontrar o valor de α, basta dividir 72 por 2.
α = 72º : 2
α = 36º
-
Ângulo excêntrico interno
Um ângulo é conhecido como excêntrico interno quando ele não está no centro da circunferência, mas está localizado na parte interior da circunferência, não podendo ser um ângulo inscrito. Quando isso ocorre, podemos definir dois arcos. O ângulo será a média aritmética entre eles, ou seja, a soma dividida por dois.
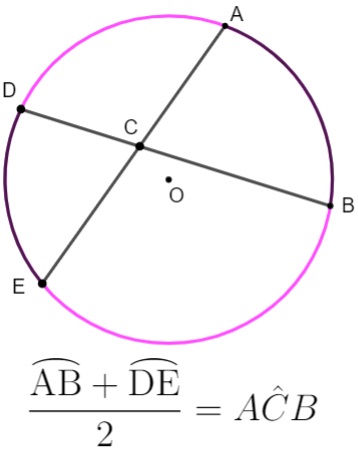
Exemplo:
Calcule o valor do ângulo α na circunferência sabendo que C não é o centro da circunferência.
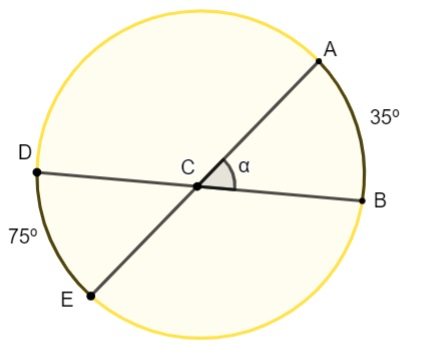
![]()
Acesse também: Como construir polígonos circunscritos?
-
Ângulo excêntrico externo
Conhecemos como excêntrico externo o ângulo que é externo à circunferência. Quando isso ocorre, ele forma dois arcos, e o valor do ângulo é calculado pela metade da diferença entre o arco maior e o arco menor.
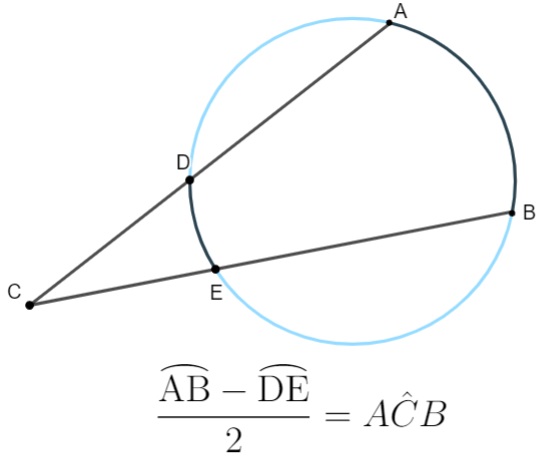
Exemplo:
Calcule o valor do ângulo α.
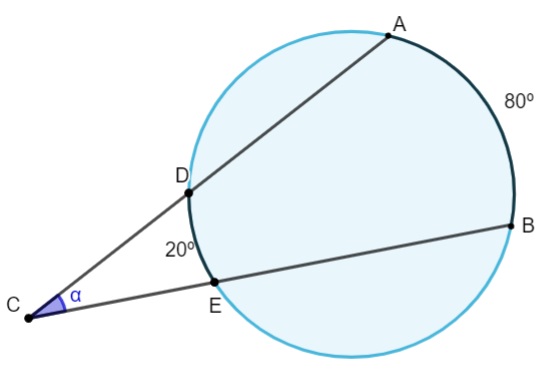
![]()
-
Ângulos de segmento
O ângulo é conhecido como ângulo de segmento quando ele é formato por um segmento de reta tangente à circunferência e o outro não. Quando isso ocorre, o ângulo é igual à metade do arco.
Exemplo:
Qual é o valor do ângulo α na circunferência a seguir?
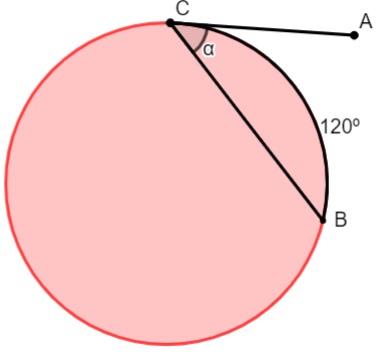
Analisando a imagem, sabemos que o ângulo α é igual à metade do arco, ou seja, metade de 120º, então α = 60º.
Veja também: Cálculos e fórmula da equação reduzida da circunferência
Exercícios resolvidos
Questão 1 – Podemos afirmar que o valor do ângulo BÂC no triângulo a seguir é:
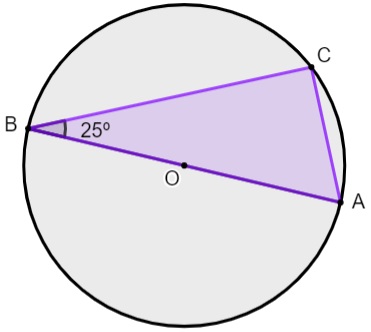
A) 60º
B) 65º
C) 70º
D) 75º
E) 90º
Resolução
Alternativa B.
Analisando a circunferência, o arco formado pelos pontos AB tem amplitude igual à meia circunferência, ou seja, 180º.Como o ângulo C é inscrito, então ele corresponde à metade de 180º, logo o ângulo C é igual a 90º.
A soma dos ângulos internos do triângulo é sempre igual a 180º, então temos que:
25º + BÂC + 90º = 180º
BÂC = 180º – 90º – 25º
BÂC = 90º – 25º
BÂC = 65º
Questão 2 – Calcule o valor de x na circunferência a seguir.
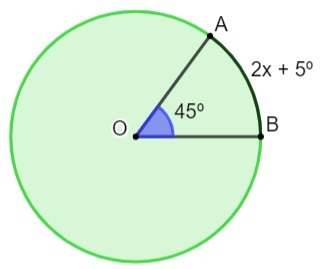
A) 10
B) 15º
C) 20º
D) 40º
E) 45º
Resolução
Alternativa C.
Sabendo que AÔB é o ângulo central e que ele corresponde ao valor do arco, então temos que:
2x + 5º = 45º
2x = 45º – 5º
2x = 40º
x = 40º: 2
x = 20º


