Área de sólidos geométricos

A área de um sólido geométrico pode ser obtida pela soma das áreas de cada uma das figuras geométricas que o compõem. Um tetraedro, por exemplo, é uma pirâmide de base triangular. Essa pirâmide é formada por quatro triângulos: uma base e três faces laterais. Somando as áreas de cada um desses triângulos, teremos a área do tetraedro.
 

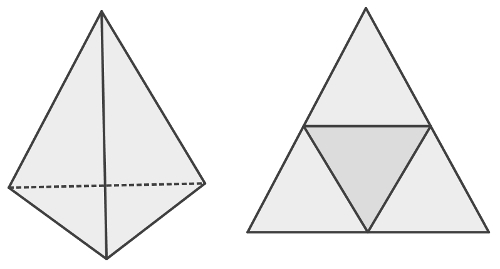
                                                                                           Tetraedro regular à direita e sua planificação à esquerda

A seguir veja as fórmulas usadas para o cálculo de área de alguns sólidos geométricos e exemplos de como usá-las.

Tópicos deste artigo

• 1 - Área do paralelepípedo
• 2 - Área do cilindro
• 3 - Área do cone
• 4 - Área da esfera
• 5 - Área da pirâmide
• 6 - Área do prisma

Área do paralelepípedo

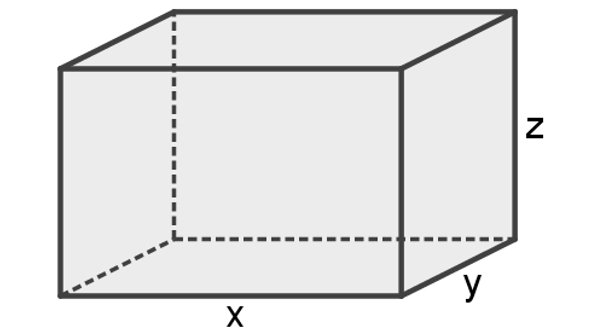
Considere um paralelepípedo cujo comprimento mede “x”, a largura mede “y” e a altura mede “z”, como o da figura a seguir:
 

A fórmula usada para calcular sua área é:

A = 2xy + 2yz + 2xz

Essa mesma fórmula vale para a área do cubo, que é um caso especial de paralelepípedo. Entretanto, como todas as arestas do cubo são iguais, essa fórmula pode ser reduzida. Assim, a área de um cubo de aresta L é determinada por:
 

A = 6L²

Exemplo 1

Qual é a área de um bloco retangular com comprimento e largura iguais a 10 cm e com altura igual a 5 cm?

Como comprimento = largura = 10 cm, teremos x = 10 e y = 10. Como altura = 5 cm, teremos z = 5. Usando a fórmula da área do paralelepípedo, teremos:
 

A = 2xy + 2yz + 2xz

A = 2·10·10 + 2·10·5 + 2·10·5

A = 200 + 100 + 100

A = 400 cm²

Exemplo 2

Qual a área de um cubo cuja aresta mede 10 cm?

A = 6L²

A = 6·10²

A = 6·100

A = 600 cm²

Área do cilindro

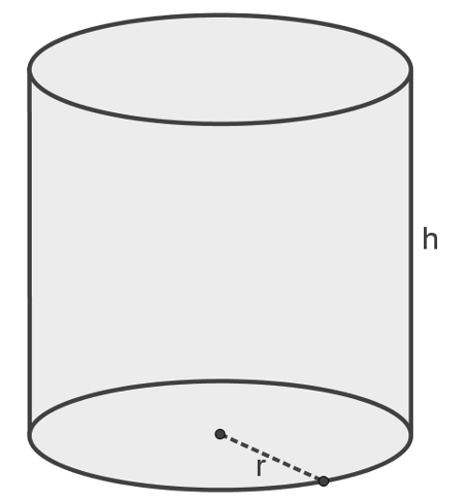
Dado o cilindro de raio r e altura h, ilustrado pela figura a seguir, a fórmula usada para calcular sua área é:

A = 2πr(r + h)

Exemplo 3

Determine a área de um cilindro cuja altura mede 40 cm e o diâmetro mede 16 cm. Considere π = 3.

O raio de um círculo é igual à metade de seu diâmetro (16:2 = 8). Assim, o raio da base do cilindro é igual a 8 cm. Basta substituir esses valores na fórmula:
 

A = 2πr(r + h)

A = 2·3·8(8 + 40)

A = 2·3·8·48

A = 6·384

A = 2304 cm²

Área do cone

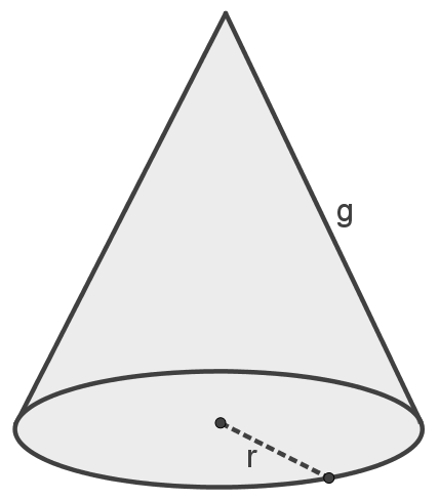
A fórmula usada para determinar a área do cone é:

A = πr(r + g)
 

A figura a seguir mostra que r é o raio do cone e g é a medida de sua geratriz.
 

Exemplo 4

Calcule a área de um cone cujo diâmetro é igual a 24 cm e cuja altura mede 16 cm. Considere π = 3.

Para descobrir a medida da geratriz do cone, use a seguinte expressão:
 

g² = r² + h²
 

Como o raio do cone é igual à metade de seu diâmetro, a medida do raio é 24:2 = 12 cm. Substituindo os valores na expressão, teremos:
 

g² = r² + h²

g² = 12² + 16²

g² = 144 + 256

g² = 400

g = √400

g = 20 cm

Substituindo a medida do raio e da geratriz do cone na fórmula de área, teremos:
 

A = πr(r + g)

A = 3·12(12 + 20)

A = 36·32

A = 1152 cm²

Área da esfera

A fórmula usada para calcular a área da esfera de raio r é:

A = 4πr²

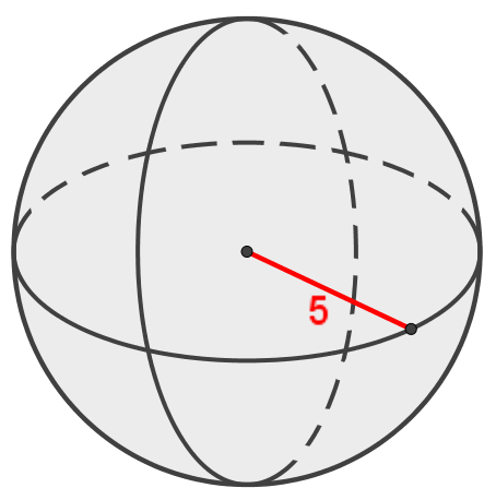
Exemplo 5

Calcule a área da esfera da imagem a seguir. Considere π = 3.

Usando a fórmula da área da esfera, teremos:

A = 4πr²

A = 4·3·5²

A = 12·25

A = 300 cm²

Área da pirâmide

Os prismas e pirâmides não possuem uma fórmula específica para cálculo de área, pois o formato de suas faces laterais e de suas bases é muito variável. Entretanto, é sempre possível calcular a área de um sólido geométrico planificando-o e somando as áreas individuais de cada uma de suas faces.

Quando esses sólidos são retos, como o prisma reto e a pirâmide reta, é possível identificar relações entre as medidas de suas faces laterais.

Veja também: Cálculo da área de um prisma

Exemplo 6

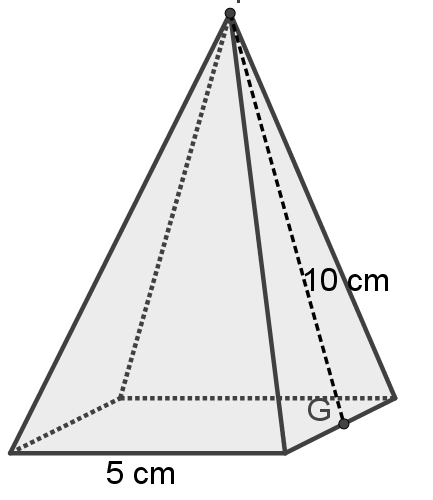
Uma pirâmide reta de base quadrada possui apótema igual a 10 cm e aresta da base igual a 5 cm. Qual é a sua área?

Para resolver esse exemplo, observe a imagem da pirâmide a seguir:
 

Uma pirâmide reta de base quadrada possui todas as faces laterais congruentes. Assim, basta calcular a área de uma delas, multiplicar o resultado por 4 e somar isso ao resultado obtido no cálculo da área da base da pirâmide.

Para calcular a área de um desses triângulos, precisamos da medida de sua altura. Essa medida é igual ao apótema da pirâmide, portanto, 10 cm. Na fórmula a seguir, o apótema será representado pela letra h. Além disso, todas as bases dos triângulos são congruentes, pois todas elas são também lados de um quadrado e medem 5 cm.

Área de uma face lateral:

A =  bh 
      2

A =  5·10 
      2

A =  50 
      2

A = 25 cm²

Área das quatro faces laterais:

A = 4·25

A = 100 cm²

Área da base (que é igual à área de um quadrado):

A = l²

A = 5²

A = 25 cm²

Área total dessa pirâmide:

A = 100 + 25 = 125 cm²

Área do prisma

Como dito, não há fórmula específica para a área do prisma. Devemos calcular a área de cada uma de suas faces e somá-las no final.

Exemplo 7

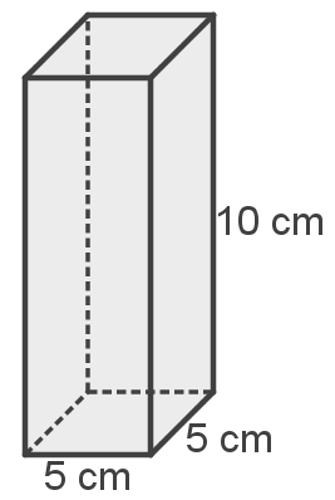
Qual é a área do prisma reto de base quadrada, sabendo que a altura desse sólido é de 10 cm e que a aresta de sua base mede 5 cm?

Solução:

A seguir, veja uma imagem do prisma em questão para auxiliar na construção da solução:
 

O exercício informa que a base do prisma é quadrada. Além disso, as duas bases do prisma são congruentes, ou seja, encontrando a área de uma dessas bases, basta multiplicar essa medida por 2 para determinar a área das duas bases do prisma.

A_b = l²

A_b = 5²

A_b = 25 cm²

Além disso, como ele possui base quadrada, fica fácil perceber que ele possui quatro faces laterais, que também são congruentes, pois o sólido é reto. Assim, encontrando a área de uma das faces laterais, basta multiplicar esse valor por 4 para encontrar a área lateral do prisma.

A_fl = b·h

A_fl = 5·10

A_fl = 50 cm²

A_l = 4A_fl

A_l = 4·50

A_l = 200 cm²

A área total do prisma é:

A = A_b + A_l

A = 25 + 200

A = 225 cm²

Por Luiz Paulo Silva
Graudado em Matemática