Quadrados

Para ser considerada um quadrado, a figura geométrica plana deve possuir as três características a seguir:

• deve ser um polígono com quatro lados;

• todos os quatro lados devem ser iguais;

• todos os ângulos internos devem ser retos.

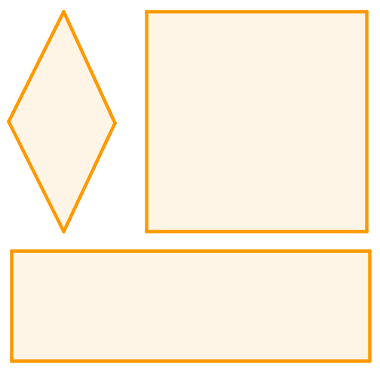
Exemplo de losango, quadrado e retângulo

Observe que os losangos são figuras geométricas que possuem quatro lados iguais, mas podem ter ângulos de qualquer tamanho, respeitadas as devidas proporções. Já os retângulos são figuras cujos ângulos internos são retos, mas que não necessariamente possuem os quatro lados iguais.

Elementos de um quadrado

Todo polígono possui os elementos listados a seguir. Como os quadrados são polígonos que possuem quatro lados, não é diferente para eles.

• Lados: segmentos de reta que caracterizam o quadrado;

• Vértices: Pontos de encontro entre dois lados;

• Ângulos internos: os ângulos retos;

• Diagonais: Segmentos de reta cujas extremidades são dois vértices de um polígono, mas que não são lados.

• Ângulos externos: Ângulos formados pelo prolongamento de um dos lados de um polígono e o lado adjacente a ele. Existe uma propriedade que garante que a soma de um ângulo interno e um ângulo externo adjacente a ele é igual a 180°. Sendo assim, todos os ângulos externos de um quadrado medem 90° também.

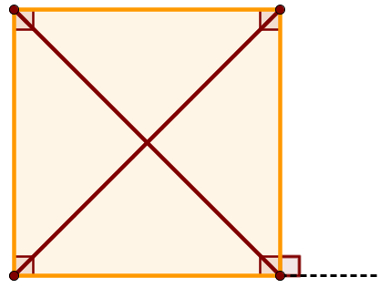
Quadrado com seus elementos observados em qualquer polígono

Quadrados e paralelogramos

Todo quadrilátero que possui lados opostos paralelos é um paralelogramo. Também é possível identificar essas figuras da seguinte maneira: todo quadrilátero que possui lados iguais é um paralelogramo.

Assim, todo quadrado é também paralelogramo, entretanto, nem todo paralelogramo é quadrado, porque não é necessário ter lados nem ângulos congruentes para ser paralelogramo.

As características dos paralelogramos, portanto, são todas herdadas dos quadrados. Entretanto, apenas uma delas não é óbvia. Observe:

• Todo paralelogramo possui lados opostos paralelos e congruentes. Como o quadrado possui todos os lados congruentes, é evidente que os seus lados opostos são congruentes também;

  Não pare agora... Tem mais depois da publicidade ;)

• Todo paralelogramo possui ângulos opostos congruentes. Para os quadrados, a justificativa dessa propriedade é igual à justificativa anterior;

• Em todo paralelogramo as diagonais cruzam-se em seus pontos médios. Como os quadrados são paralelogramos, suas diagonais cruzam-se em seus pontos médios.

Quadrados são losangos e retângulos ao mesmo tempo

As respectivas definições de losango e retângulo são: paralelogramo que possui lados congruentes e paralelogramo que possui ângulos retos. Como o quadrado tem as duas características ao mesmo tempo, ele é, portanto, losango e retângulo.

Dessa maneira, as afirmações a seguir são válidas:

• Todo quadrado é retângulo;

• Todo quadrado é losango;

• Nem todo losango é quadrado (nem todo losango possui ângulos retos);

• Nem todo retângulo é quadrado (nem todo retângulo possui todos os lados congruentes).

As propriedades específicas que os quadrados herdam dessas figuras são:

• Em todo losango, as diagonais são perpendiculares;

• Em todo retângulo, as diagonais são congruentes.

Sendo assim, a seguinte propriedade é válida:

Em todo quadrado, as diagonais são congruentes e perpendiculares.

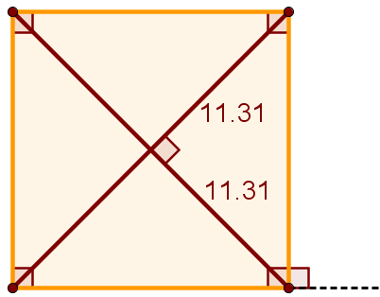
Área e perímetro dos quadrados

O perímetro é a medida do contorno de uma figura geométrica. No caso específico dos polígonos, é permitido somar as medidas dos seus lados para encontrar o perímetro. Como as medidas dos lados de um quadrado são iguais e ele possui quatro lados, a seguinte expressão resolve o problema do perímetro:

P = 4·l

P = perímetro do quadrado e l = medida do lado do quadrado. Essa expressão foi obtida pela soma dos lados do quadrado, pois l + l + l + l = 4l

A área de um paralelogramo é o produto da base pela altura. Como a base e a altura do quadrado são iguais, para calcular sua área, basta usar a seguinte expressão:

A = l²

l também é o lado do quadrado. Essa expressão foi obtida após multiplicar o valor da base do quadrado pela sua altura. Observe:

A = b·h = l·l = l²

Por Luiz Paulo Moreira
Graduado em Matemática