PUBLICIDADE
Os polígonos são figuras geométricas planas formadas por segmentos de reta. Os elementos de um polígono são os objetos matemáticos que fazem parte de sua estrutura: pontos, retas e ângulos. Polígonos convexos possuem elementos a mais que polígonos não convexos, além de algumas propriedades também exclusivas.
Antes de apresentarmos os elementos e propriedades, é importante realizar a definição formal dos polígonos. Vamos lá?
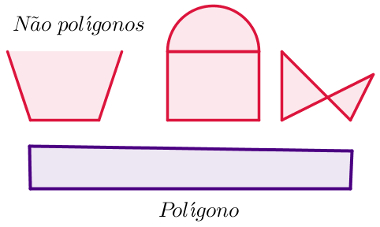
Definição de polígono
Um polígono é uma figura geométrica plana que possui as seguintes características:
-
É formado apenas por segmentos de reta;
-
É fechado;
-
Esses segmentos de reta não se cruzam.
Além disso, uma figura que possui outro ponto de encontro entre segmentos de reta, que não seus extremos, pode ser vista como um conjunto de polígonos, mas não como um polígono único.
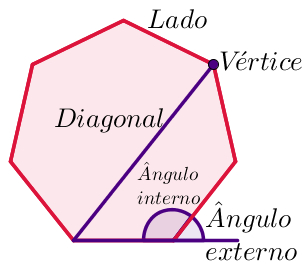
Elementos de um polígono convexo
Todo polígono convexo possui os seguintes elementos:
-
Lados: são os segmentos de reta que determinam o polígono;
-
Vértices: são os pontos de encontro entre dois lados;
Não pare agora... Tem mais depois da publicidade ;) -
Diagonais: segmentos de reta que ligam dois vértices não consecutivos de um polígono. Os segmentos de reta que ligam dois vértices consecutivos são os lados;
-
Ângulos internos: são os ângulos formados, no interior do polígono, por dois segmentos de reta adjacentes;
-
Ângulos externos: São os ângulos formados, no exterior de um polígono, pelo prolongamento de um lado e o lado adjacente a ele;
Propriedades dos polígonos convexos
-
O número de lados, vértices e ângulos (internos e externos) é o mesmo.
-
A soma dos ângulos internos de um polígono convexo de n lados pode ser obtida pela seguinte expressão:
S = (n – 2)·180
-
O número de diagonais de um polígono convexo de n lados pode ser obtido pela seguinte expressão:
d = n(n – 3)
2
-
A soma das medidas dos ângulos externos de um polígono convexo qualquer não depende do seu número de lados e é sempre igual a 360°.
Por Luiz Paulo Moreira
Graduado em Matemática