Ângulos

O ângulo é uma região delimitada por duas semirretas. Para medi-lo, há duas possíveis unidades: grau ou radiano. De acordo com a sua medida, ele pode ser classificado em agudo, reto, obtuso ou raso.

Quando temos dois ângulos, podemos estabelecer relações entre eles. Caso eles possuam a mesma medida, eles são chamados de congruentes. Quando a soma entre eles é igual a 90º ou 180º ou 360º, eles são conhecidos, respectivamente, como ângulos complementares, suplementares e replementares.

Leia também: Ângulos notáveis – conheça os ângulos mais usados na trigonometria

Tópicos deste artigo

• 1 - Como medir um ângulo
• 2 - Unidade de medida de ângulos
• 3 - Classificação dos ângulos
• 4 - Ângulos congruentes
• 5 - Ângulos opostos pelo vértice
• 6 - Bissetriz de um ângulo
• 7 - Ângulos consecutivos e ângulos adjacentes
• 8 - Casos particulares de soma de dois ângulos
  • → Ângulos complementares
  • → Ângulos suplementares
  • → Ângulos replementares
• 9 - Retas paralelas cortadas por uma transversal
• 10 - Exercícios resolvidos

Como medir um ângulo

Para a realização de um desenho ou para a medição de um ângulo, na geometria plana utilizamos o compasso e o transferidor. Existem alguns outros instrumentos utilizados por profissionais da construção civil, como o teodolito.

Como o ângulo corresponde à região que está entre duas semirretas, para realizar a medida em um transferidor, posicionamos uma das semirretas apontando para 0º e observamos o grau para o qual a outra semirreta está apontada.

Unidade de medida de ângulos

Existem duas possibilidades para medirmos um ângulo: o grau e o radiano. 1 rad é o ângulo que faz com que o arco formado na circunferência tenha a mesma medida que o raio dessa circunferência.

É bastante comum a necessidade de converter graus para radianos. Para isso, utilizamos regra de três, sabendo sempre que 180º corresponde a π.

Exemplo

- Qual é o valor de um ângulo de 60º em radianos?

Resolução:

π rad ------------------------- 180º

x rad ------------------------- 60º

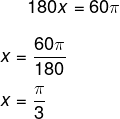
Agora, para converter de radianos para graus, basta realizarmos a substituição de π por 180º.

Exemplo

- Qual é o valor do ângulo que mede a terça parte de 2π rad em graus?

Classificação dos ângulos

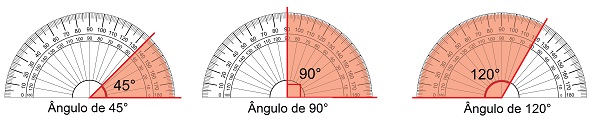
Um ângulo pode ser classificado de acordo com a sua medida. Além de nulo (ângulo de 0º), um ângulo pode ser agudo, reto, obtuso, raso, côncavo ou inteiro.

• Ângulo agudo: quando sua medida é um número maior que 0 e menor que 90º.

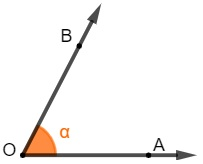
Note que o ângulo AÔB, representado também por α, é um ângulo maior que 0º e menor que 90º.

• Ângulo reto: possui exatamente 90º. Quando isso acontece, podemos dizer também que as semirretas se cruzam de forma perpendicular.

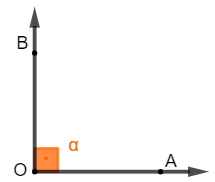
Geralmente o ângulo reto possui a região angular (região em laranja na imagem) representada por um quadrado.

• Ângulo obtuso: quando sua medida é maior que 90º e menor que 180º.

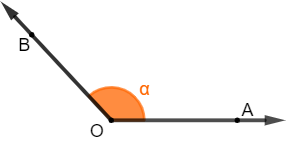
• Ângulo raso: conhecido também como meia-volta ou meia-lua, esse ângulo equivale à metade de um ângulo inteiro, logo possui exatamente 180º.

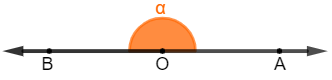
• Ângulo côncavo: menos comum nas situações cotidianas que os demais, é o ângulo que tem medida maior que 180º e menor que 360º.

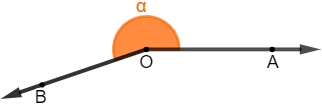
• Ângulo inteiro: como o nome sugere, esse ângulo representa a volta completa, possuindo exatamente 360º.

Leia também: Polígonos – figuras geométricas formadas por segmentos de reta

Ângulos congruentes

Dois ângulos são chamados de congruentes quando possuem a mesma medida. Esse conceito é muito confundido com a ideia de igualdade. Para que os ângulos sejam congruentes, eles não precisam ser necessariamente iguais, mas precisam ter a mesma medida.

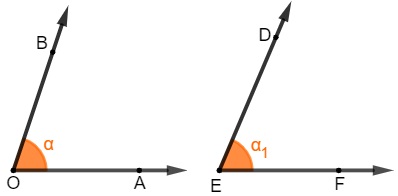
Ângulos opostos pelo vértice

Um caso bastante comum de ângulos congruentes é quando os ângulos são opostos pelo vértice. Quando temos duas retas concorrentes, ou seja, que se cruzam, é possível traçarmos vários ângulos entre elas. Quando comparamos dois ângulos que estão em lados opostos de um mesmo vértice, eles sempre serão congruentes, ou seja, terão a mesma medida.

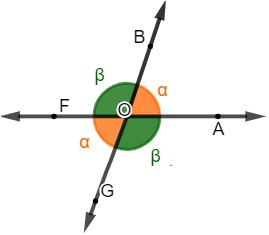
Leia também: Ângulos colaterais internos e externos

Bissetriz de um ângulo

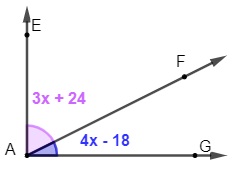
Definimos como bissetriz de um ângulo a semirreta que divide o ângulo em duas partes congruentes, ou seja, de mesma medida.

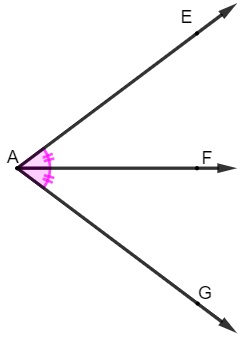
A bissetriz AF divide o ângulo maior EÂG em dois ângulos congruentes. O ângulo EÂF é congruente ao ângulo FÂG.

Ângulos consecutivos e ângulos adjacentes

Dois ângulos são consecutivos quando possuem o mesmo vértice e um de seus lados em comum. O conceito de ângulo adjacente, muitas vezes, confunde-se com o de ângulo consecutivo, porém possuem uma diferença sutil – a começar pelo fato de que ângulos adjacentes são casos particulares de ângulos consecutivos.

Dois ângulos consecutivos são adjacentes quando eles possuem somente o lado e o vértice em comum, mas nenhuma região pode pertencer aos dois ao mesmo tempo.

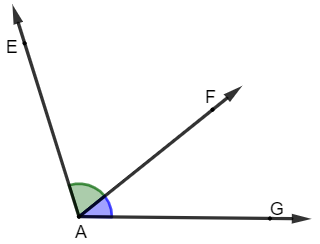
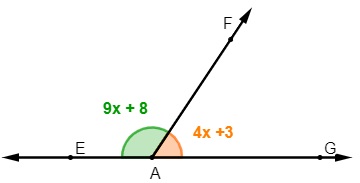
Na representação acima, podemos encontrar ângulos consecutivos e ângulos consecutivos adjacentes. Os ângulos EÂG e EÂF são consecutivos, pois possuem em comum o lado EA e o vértice A. Perceba que, nesse caso, o ângulo EÂF está contido no ângulo maior EÂG, o que faz com que eles não sejam adjacentes.

Os ângulos EÂF e FÂG também são consecutivos, pois possuem o lado FA em comum e também o vértice A, porém, nesse caso, eles possuem somente isso em comum, o que faz com que eles sejam consecutivos e adjacentes.

Casos particulares de soma de dois ângulos

Existem três casos particulares para a soma entre dois ângulos, de acordo com o resultado dessa soma. São eles: ângulos complementares, ângulos suplementares e ângulos replementares.

→ Ângulos complementares

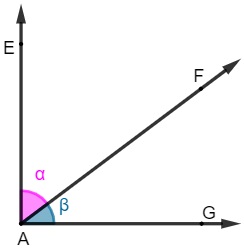
Dois ângulos são conhecidos como complementares quando o resultado da soma dos dois é igual a 90º, ou seja, juntos eles formam um ângulo reto.

→ Ângulos suplementares

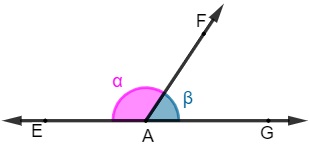
Dois ângulos são considerados suplementares quando a soma entre eles é igual a 180º, ou seja, juntos eles formam um ângulo raso.

→ Ângulos replementares

 

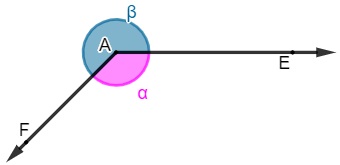
Menos comum que os anteriores em livros didáticos e provas, o ângulo replementar ocorre quando a soma de dois ângulos gera um ângulo inteiro, ou seja, um ângulo de medida igual a 360º.

Retas paralelas cortadas por uma transversal

Quando há duas retas paralelas cortadas por uma transversal, é possível estabelecer uma relação importante entre os ângulos formados na reta. Há três informações importantes que te auxiliam a descobrir o valor de todos os oito ângulos nessa situação. Veja:

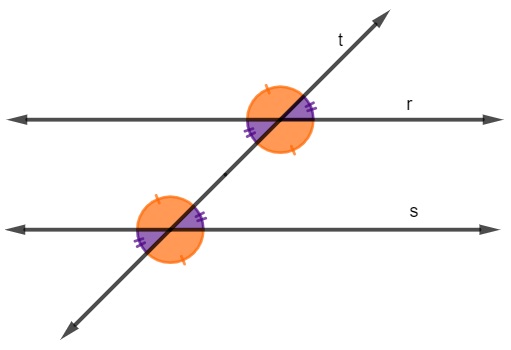
• Os ângulos agudos são sempre congruentes;

• Os ângulos obtusos são sempre congruentes.

A soma de um agudo com um obtuso é igual a 180º, ou seja, eles são suplementares.

Essas três informações nos permitem, por meio de equações, descobrir o valor de todos os oito ângulos quando há duas retas paralelas cortadas por uma transversal.

Leia também: Seno e cosseno de ângulos suplementares

Exercícios resolvidos

Questão 1 - (IFG) Supondo que a'//a e b'//b, marque a alternativa correta.

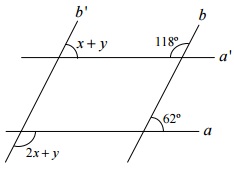
a) x = 31° e y = 31°

b) x = 56° e y = 6°

c) x = 6° e y = 32°

d) x = 28° e y = 34°

e) x = 34° e y = 28°

Resolução:

Analisando a figura, temos dois ângulos agudos e dois ângulos obtusos.
Como o enunciado nos informa que são retas paralelas cortadas por uma transversal, os ângulos agudos e os obtusos são congruentes, então temos que:

Seja 2x + y = 118º a equação I e x+y = 62 º a equação II, vamos resolvê-las pelo método da adição, multiplicando a equação II por ( -1).

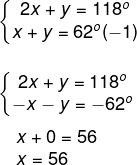
Conhecendo o valor de x, vamos substitui-lo na equação II.

x+y = 62º

56º + y =62º

y=62º – 56º

y = 6º

Alternativa B.

Questão 2 - Dois ângulos são suplementares. Sabendo que um é o dobro do outro, qual é o valor do menor ângulo?

a) 120º

b) 90º

c) 180º

d) 60º

e) 30º

Resolução:

Se esses ângulos são suplementares, a soma é igual a 180º. Assim, seja x o menor, então o maior é 2x.

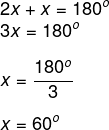
Alternativa D.

 

Por Raul Rodrigues de Oliveira
Professor de Matemática