Operações com frações

Operações com frações, isto é, com o conjunto dos números racionais, fazem parte de um conjunto fechado para as operações de adição, subtração, multiplicação e divisão.

Em matemática, quando dizemos que um conjunto é fechado para alguma operação, queremos dizer que quando operamos dois elementos quaisquer desse conjunto o resultado ainda permanece nele, ou seja, quando realizamos qualquer operação entre frações, o resultado ainda é uma fração.

Leia também: Números mistos: saiba como resolver problemas com eles!

Adição de frações

A ideia de adição de frações é idêntica à de adição de números inteiros. Para melhor entendermos o primeiro tipo, vamos comparar as imagens seguintes.

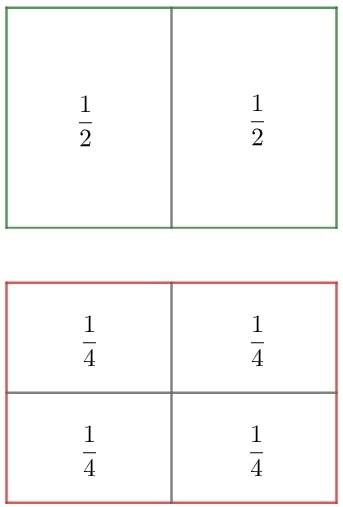
Perceba duas partes de 1/4 equivalem a 1/2. Ou seja:

A utilização de elementos gráficos auxilia no entendimento de como somar frações, entretanto, não é conveniente fazer desenhos toda vez que desejamos somar duas ou mais dessas.

Do último exemplo, veja que se calcularmos o mínimo múltiplo comum dos denominadores, dividirmos esse número em seguida pelos denominadores e depois multiplicarmos o que restou pelos numeradores, obteremos 1/2. Confira:

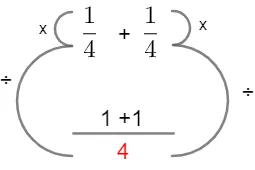
Subtração de frações

A ideia de subtração é praticamente idêntica à da operação de adição. Utilizaremos o mesmo processo algébrico, entretanto, em vez de somar os denominadores, iremos subtrai-los. Veja:

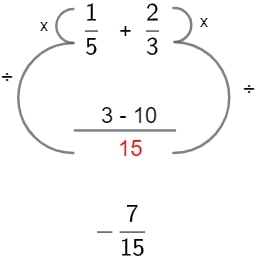
Leia também: Redução de fração ao mesmo denominador

Multiplicação de frações

A multiplicação entre frações consiste em multiplicar numerador com numerador e, em seguida, denominador com denominador delas. De forma geral, a multiplicação fica assim:

Não se esqueça de que, ao final de todas as frações, devemos simplificá-las se possível. Veja o exemplo:

Divisão de frações

Na divisão de fração, devemos conservar (manter) a primeira fração e multiplicá-la pelo inverso da segunda. Sua forma geral fica da seguinte maneira:

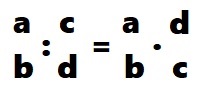
A divisão de frações apresenta duas notações, ou seja, duas maneiras diferentes de representar a mesma ideia, são elas:

Exemplo:

Exercícios resolvidos

Questão 1 - Some 3/5 com 3/6, e divida o resultado obtido pelo inverso do número 30.

Solução:

Inicialmente devemos somar as frações do enunciado, assim:

Agora, segundo o enunciado, devemos dividir esse resultado pelo inverso de 30, ou seja, 1/30. Assim:

Resultado = 43

Questão 2 - O que acontece ao multiplicar-se uma fração qualquer pelo seu inverso?

Solução

Note que temos duas maneiras de pensar esse exercício. A primeira delas: multiplicar uma fração pelo inverso é o mesmo que dividi-la. Assim, dividindo dois números iguais, o resultado só pode ser igual a 1. A segunda: multiplicar uma fração pelo seu inverso, veja: 

Por Robson Luiz
Professor de Matemática