PUBLICIDADE
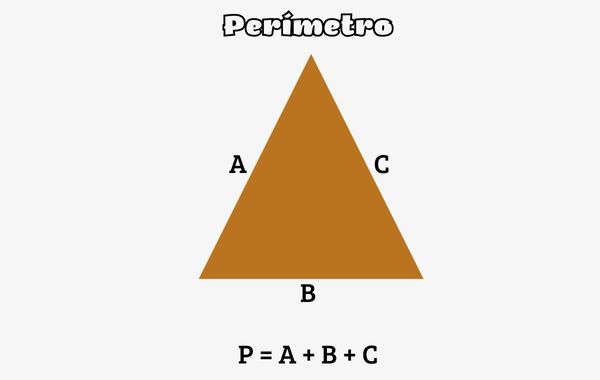
O perímetro é a medida do contorno de um polígono. Para obter o perímetro, calculamos a soma de todos os lados do polígono. Como o perímetro é a medida do comprimento do contorno, ele é medido em metros, centímetros, quilômetros ou qualquer múltiplo ou submúltiplo do metro.
Veja também: Classificação de polígonos
Tópicos deste artigo
- 1 - O que é o perímetro?
- 2 - Unidade de medida do perímetro
- 3 - Como calcular o perímetro?
- 4 - Diferença entre perímetro e área
- 5 - Exercícios resolvidos sobre perímetro
O que é o perímetro?
O perímetro é o comprimento do contorno de um polígono (figura plana e fechada), logo, para calcular o perímetro, basta somarmos a medida de todos os lados desse polígono.
Unidade de medida do perímetro
Como o perímetro é uma medida linear, ou seja, com só uma dimensão, e é uma medida de comprimento, ele tem como unidade fundamental o metro, podendo ser escrito também como um múltiplo ou um submúltiplo do metro — por exemplo, um perímetro de 20 km ou um perímetro de 15 cm.
Como calcular o perímetro?
Para calcular o perímetro de um polígono, basta calcular a soma dos seus lados. Veja a seguir o perímetro de um polígono qualquer, o perímetro de um polígono regular e o perímetro de uma circunferência.
→ Perímetro de um polígono qualquer
De modo geral, se conhecemos a medida dos lados do polígono, basta somar os lados para encontrar a medida do perímetro desse polígono.
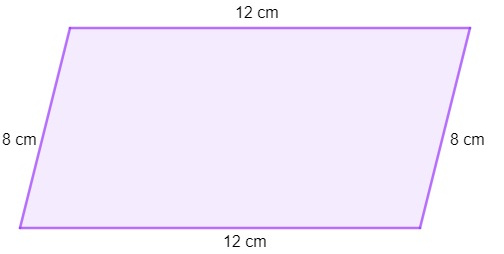
O perímetro desse polígono é:
P = 8 + 12 + 8 + 12 = 40 cm
→ Perímetro de um polígono regular
O polígono é classificado como regular quando ele possui todos os lados congruentes, ou seja, todos os lados com a mesma medida. Quando o polígono é regular, para calcular o seu perímetro basta multiplicar a medida de um dos lados pela quantidade de lados.
- Exemplo:
Qual é o perímetro de um pentágono regular cuja medida do lado é de 13 cm?
Resolução:
O pentágono é um polígono que possui 5 lados. Sendo assim, para calcular o seu perímetro temos que:
\(P=5l\)
Como a medida do lado é 13:
\(P=5⋅13\)
\(P=65\ cm\)
→ Perímetro de uma circunferência
Na circunferência, o que conhecemos como perímetro para os polígonos chamamos de comprimento da circunferência, ou seja, o comprimento da circunferência é o comprimento do contorno de um círculo. Para calcular o comprimento da circunferência utilizamos a fórmula que depende do comprimento do raio r:
\(C=2πr\)
- Exemplo:
Calcule o comprimento da circunferência:
(Use π = 3.)
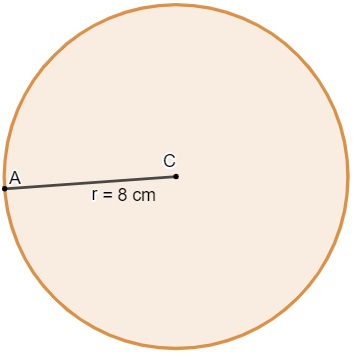
Resolução:
A circunferência possui raio medindo 8 cm, então o seu comprimento será de:
\(C=2πr\)
\(C=2⋅3⋅8\)
\(C=6⋅8\)
\(C=48\ cm\)
Diferença entre perímetro e área
Sendo outra medida importante de uma figura plana, a área se difere do perímetro por ser a medida da superfície da figura plana, e não só do contorno, como é o perímetro. A unidade de medida de área são unidades quadradas, já que ela possui duas dimensões, ou seja, o metro quadrado (m²), os seus múltiplos e os seus submúltiplos. Vale ressaltar que tanto a área quanto o perímetro são grandezas igualmente importantes utilizadas para compreender melhor as características da figura plana.
Leia também: Volume dos sólidos geométricos — uma grandeza tridimensional
Exercícios resolvidos sobre perímetro
Questão 1
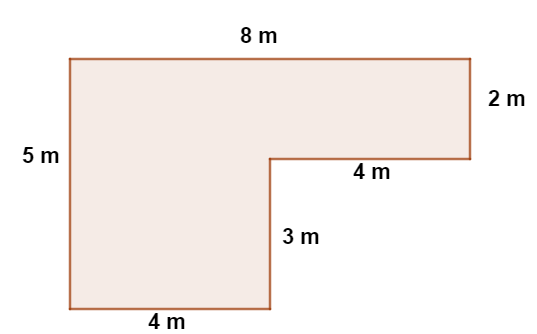
Para proteger a sua plantação de milho, Seu Geraldo decidiu cercar o terreno da área plantada com quatro fios de arame farpado.
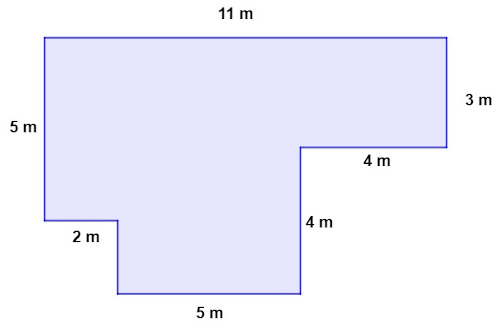
A metragem mínima necessária de arame farpado para cercar o terreno da forma que o Seu Geraldo deseja é de:
A) 88 m
B) 96 m
C) 132 m
D) 144 m
E) 196 m
Resolução:
Alternativa D
Calculando o perímetro do terreno:
P = 5 + 2 + 2 + 5 + 11 + 3 + 4 + 4 = 36 m
Como ele vai dar 4 voltas:
\(36⋅4=144\ m\)
Questão 2
O perímetro de um triângulo é 35 cm. Se os seus lados medem 2x + 4, 4x – 10 e 3x + 5, o valor de x é:
A) 2
B) 3
C) 4
D) 5
E) 6
Resolução:
Alternativa C
Calculando o perímetro, temos que:
\(2x+4+4x-10+3x+5=35\)
\(2x+4x+3x-1=35\)
\(9x=35+1\)
\(9x=36\)
\(x=\frac{36}9\)
\(x=4\)
Por Raul Rodrigues de Oliveira
Professor de Matemática
