Área do quadrado

A área do quadrado é a medida de sua superfície e pode ser calculada elevando seu lado ao quadrado. O quadrado é um quadrilátero que possui todos os lados congruentes, ou seja, com a mesma medida, o que faz dele um caso particular de quadrilátero.

Assim como em retângulos, a área do quadrado é igual ao produto entre a sua base e a sua altura, mas como no quadrado a base e a altura são congruentes, então podemos calcular a sua área elevando a medida do lado ao quadrado.

Leia também: Área do triângulo retângulo — como calcular?

Tópicos deste artigo

• 1 - Resumo sobre área do quadrado
• 2 - O que é um quadrado?
• 3 - Qual a fórmula da área do quadrado?
• 4 - Como calcular a área do quadrado?
• 5 - Diferenças entre a área e o perímetro do quadrado
• 6 - Diagonal do quadrado
• 7 - Exercícios resolvidos sobre área do quadrado

Resumo sobre área do quadrado

• O quadrado é um polígono que possui 4 lados com as mesmas medidas.
• A área do quadrado é calculada elevando a medida do lado ao quadrado.
• Dado um quadrado de lado l, a sua área é dada pela seguinte fórmula:

$A=l^2$

• Além da área do quadrado, podemos calcular também o perímetro e a diagonal do quadrado, medidas tão importantes quanto a área.
• Dado um quadrado de lado l, o seu perímetro é dado pela seguinte fórmula:

$P=4l$

• Dado um quadrado de lado l, o comprimento da diagonal é dado pela seguinte fórmula:

$d=l\sqrt2$

O que é um quadrado?

O quadrado é um caso de polígono, classificado como quadrilátero, por possuir 4 lados, e como um polígono regular, por possuir todos os lados congruentes, ou seja, o quadrado é um quadrilátero que possui todos os lados com a mesma medida.

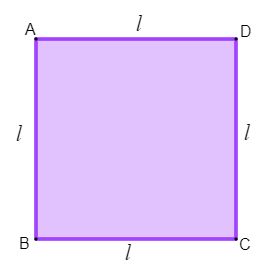
Qual a fórmula da área do quadrado?

A área é a medida da superfície de uma figura plana. Para calcular a área do quadrado, utilizamos a seguinte fórmula:

$A=l^2$

Como calcular a área do quadrado?

Multiplicamos o comprimento da sua base pela sua altura. Como, no quadrado, a base e a altura possuem a mesma medida, a área do quadrado pode ser calculada pelo quadrado do lado. Dessa forma, para calcular a área do quadrado, conhecendo a medida de seu lado, basta elevarmos a medida do lado ao quadrado, pois este possui lados congruentes e seria a mesma coisa que multiplicar o comprimento de sua base pela sua altura.

• Exemplo:

Qual é a área de um quadrado que possui lados medindo 6 cm?

Resolução:

A área desse quadrado com l = 6 é:

$A=l^2$

$A=6^2$

$A=36$

A área desse quadrado é 36 cm².

• Exemplo 2:

Calcule a área do quadrado a seguir:

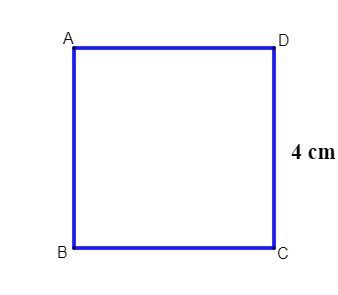
Resolução:

Sabemos que a medida do lado desse quadrado é de 4 cm, então a sua área será:

$A=l^2$

$A=4^2$

$A=16$

A área é de 16 cm².

Diferenças entre a área e o perímetro do quadrado

A área e o perímetro são duas medidas importantes de qualquer polígono, e elas representam grandezas diferentes. De modo geral, a área é a medida de superfície do polígono, ou seja, é a medida da região interna da figura plana. A medida da área possui sempre duas dimensões, e por isso temos como unidade de medida da área o metro quadrado, e os seus múltiplos e submúltiplos.

O perímetro de uma figura plana é outra grandeza importante, sendo a medida do contorno da figura. Podemos calcular o perímetro de um polígono somando a medida dos seus lados, e, diferentemente da área, o perímetro possui somente uma dimensão, a sua unidade é o metro, com os seus múltiplos e os seus submúltiplos.

• Exemplo:

Um quadrado possui lados medindo 5 metros, então qual é a medida da área e do perímetro desse quadrado?

Resolução:

Começando pela área, temos que:

$A=l^2$

$A=5^2$

$A=25\ $

Sabemos que a área é dada em unidades quadradas, logo, a área é 25 m².

Agora calcularemos o perímetro. Como o quadrado possui 4 lados congruentes, o perímetro do quadrado é igual à soma da medida dos seus quatro lados, ou seja, P = 4l. Calculando o perímetro, temos que:

$P=4l$

$P=4\cdot5$

$P=20\ m$

Diagonal do quadrado

Conhecendo a medida do lado do quadrado, outra medida importante que podemos identificar no quadrado é a da diagonal. A diagonal do quadrado é o segmento de reta que liga dois vértices não consecutivos do quadrado.

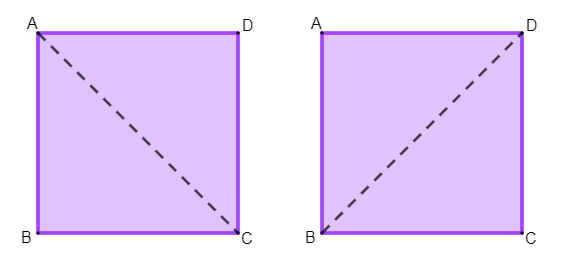
Para calcular o comprimento da diagonal, utilizamos a fórmula:

$d=l\sqrt2$

Sabendo que $\sqrt2$ é um número irracional, podemos deixar indicado o valor do lado vezes $\sqrt2$, ou, caso seja necessário, utilizar uma aproximação para o valor da $\sqrt2$.

• Exemplo:

Qual o comprimento da diagonal de um quadrado que possui lado medindo 3 cm?

Resolução:

Um quadrado possui lado medindo 3 cm, então sua diagonal medirá $3\sqrt2$ cm. Caso queiramos uma aproximação, por exemplo, utilizando $\sqrt2=1,4$, consideraremos que a medida dessa diagonal será de $3\cdot1,4=4,2\ cm$.

Veja também: Área do círculo — como calcular?

Exercícios resolvidos sobre área do quadrado

Questão 1

Um terreno que possui formato de quadrado tem área igual a 324 m². Então podemos afirmar que a medida do lado desse terreno é de:

A) 15 metros

B) 16 metros

C) 17 metros

D) 18 metros

E) 19 metros

Resolução:

Alternativa D

Sabemos que a área é igual ao quadrado da medida do lado:

$A=l^2$

Como sabemos que a área é 324 m², então temos que:

$l^2=324$

$l=\sqrt{324}$

$l=18\ $

A medida do lado desse terreno será de 18 metros.

Questão 2

Em um terreno quadrado, com lados medindo 8 metros, será colocada uma piscina, também quadrada, com lados medindo 3 metros. O restante desse terreno será gramado. Então a área a ser gramada mede:

A) 9 m²

B) 25 m²

C) 36 m²

D) 55 m²

E) 64 m²

Resolução:

Alternativa D

Calcularemos a diferença entre as áreas do terreno e da piscina, começando pela do terreno:

$A_{terreno}=8^2$

$A_{terreno}=64\ m^2$

Agora calculando a da piscina:

$A_{piscina}=3^2$

$A_{piscina}=9\ m^2\ $ 

A diferença entre elas é de 64 – 9 = 55 m².

 

Por Raul Rodrigues de Oliveira
Professor de Matemática