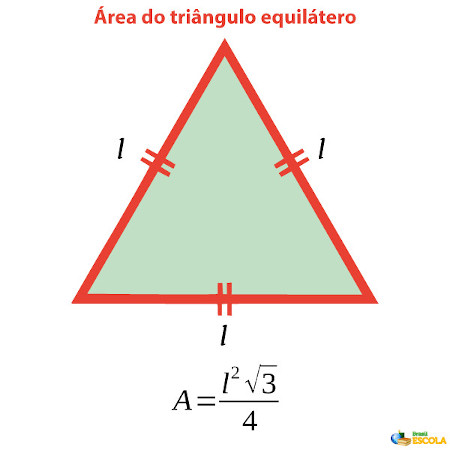
A área do triângulo equilátero pode ser calculada por uma fórmula específica desse tipo de triângulo. O triângulo é equilátero quando ele possui todos os lados com a mesma medida. Diferentemente da fórmula para calcular a área de um triângulo qualquer, que exige a medida da base e da altura do triângulo, a área do triângulo equilátero pode ser calculada conhecendo somente a medida do lado do triângulo equilátero. Para calcular a área do triângulo equilátero, multiplicamos o quadrado da medida do lado pela raiz de 3 dividido por 4.
Leia também: Área do trapézio — como calcular?
Tópicos deste artigo
- 1 - Resumo sobre área do triângulo equilátero
- 2 - Videoaula sobre área de um triângulo equilátero
- 3 - Fórmula da área do triângulo equilátero
- 4 - Como calcular a área do triângulo equilátero?
- 5 - Demonstração da fórmula da área do triângulo equilátero
Resumo sobre área do triângulo equilátero
-
O triângulo é equilátero quando ele possui os três lados congruentes, o que faz com que ele também tenha os seus ângulos congruentes.
-
A área do triângulo equilátero pode ser calculada conhecendo somente a medida do seu lado.
-
A fórmula para calcular da área do triângulo equilátero é:
\(A=\frac{l^2 \sqrt3}4\)
Videoaula sobre área de um triângulo equilátero
Fórmula da área do triângulo equilátero
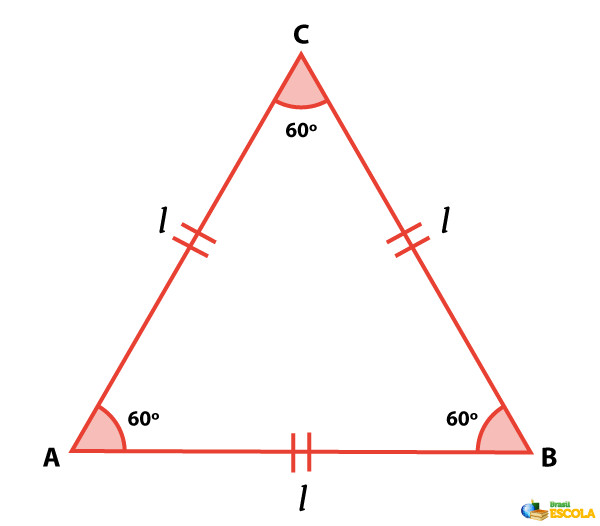
O triângulo é classificado como equilátero quando ele possui todos os lados com a mesma medida. Entre as consequências de possuir as mesmas medidas, existe também o fato de que os três ângulos são congruentes, medindo 60°.
Devido a essas características, é possível obter uma fórmula que serve para calcular a área do triângulo equilátero conhecendo apenas a medida do seu lado. A fórmula da área do triângulo equilátero é:
\(A=\frac{l^2 \sqrt3}4\)
-
l → medida do lado do triângulo equilátero.
-
A → área.
Como calcular a área do triângulo equilátero?
Para calcular a medida da área do triângulo equilátero, basta substituir na fórmula o valor de l pela medida do lado do triângulo.
-
Exemplo:
Calcule a área do triângulo equilátero que possui lados medindo 8 cm.
Resolução:
Para calcular a área do triângulo equilátero, faremos a substituição de l por 8:
\(A=\frac{8^2 \sqrt3}4\)
Após realizar a substituição, calcularemos o quadrado de 8:
\(A=\frac{64 \sqrt3}4\)
Como 64 é divisível por 4, faremos a divisão:
\(A=16\sqrt3\)
Como não temos uma aproximação para \(\sqrt3\), podemos afirmar que a área desse triângulo equilátero é igual a \(16\sqrt3\ cm^2\).
-
Exemplo 2:
Utilizando 1,7 como aproximação para \(\sqrt3\), encontre a área do triângulo equilátero:
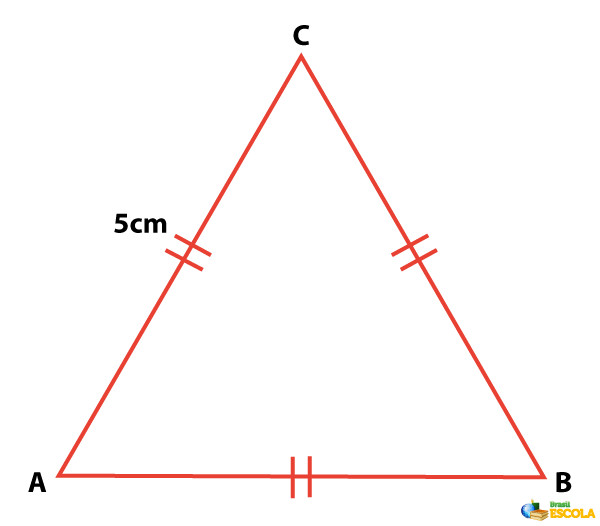
Resolução:
Substituindo l por 5 e \(\sqrt3\) por 1,7, temos que:
\(A=\frac{5^2⋅1,7}4\)
\(A=\frac{25⋅1,7}4\)
\(A=\frac{42,5}4\)
\(A=10,625\ cm^2\)
Veja também: Área do círculo — como calcular?
Demonstração da fórmula da área do triângulo equilátero
Para compreender a demonstração da fórmula da área do triângulo equilátero, é importante saber um pouco sobre a Trigonometria e a aplicação da razão seno. Para fazer a demonstração, primeiramente construiremos um triângulo equilátero de lado l:
Agora, a partir do vértice C, traçaremos a altura do triângulo em relação ao vértice C, que no triângulo equilátero é também a mediana e a bissetriz do triângulo.
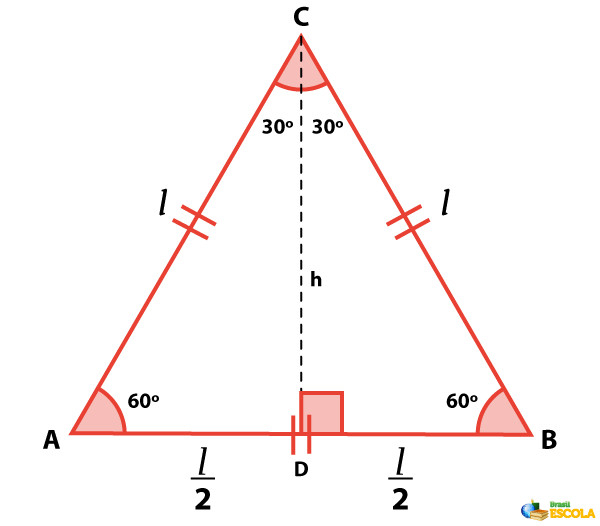
Escolhendo qualquer um dos dois ângulos da base e aplicando o seno desse ângulo, temos que:
\(sen(60°)=\frac{h}l\)
Ao consultar a tabela dos ângulos notáveis, descobrimos que o seno de 60° é igual a \(\frac{\sqrt3}{2}\):
\(\frac{\sqrt3}{2}=\frac{h}{l}\)
Então, isolando a altura:
\(h=\frac{l\sqrt3}2\)
Encontramos uma fórmula para a altura em função do lado. Sabemos que a área de um triângulo é o produto entre a base e a altura divido por 2. A base do triângulo equilátero é o seu lado, que mede l, e a altura foi encontrada acima, então temos que:
\(A=\frac{b⋅h}2\)
\(A=\frac{l⋅\frac{l\sqrt3}2}2\)
\(A=\frac{l^2 \sqrt3}{2}⋅\frac{1}2\)
\(A=\frac{l^2 \sqrt3}4\)
Fica assim demonstrada a fórmula da área do triângulo equilátero.
Por Raul Rodrigues de Oliveira
Professor de Matemática