Retas concorrentes é o nome dado para duas retas distintas que estão no mesmo plano e que se encontram em um único ponto. Quando elas se cruzam, percebe-se a formação de quatro ângulos, e, de acordo com o tamanho deles, elas podem ser perpendiculares (quando os ângulos medem 90°) ou oblíquas (quando os ângulos são diferentes de 90°). Quando as retas são concorrentes, os ângulos que estão em lados opostos, chamados de opostos pelo vértice, são sempre congruentes, ou seja, possuem a mesma medida.
Existem outras duas posições relativas possíveis para retas pertencentes a um mesmo plano, são elas as retas coincidentes (quando possuem infinitos pontos em comum) e as retas paralelas (quando não possuem nenhum ponto em comum).
Leia também: Afinal, o que é reta?
Tópicos deste artigo
- 1 - Resumo sobre retas concorrentes
- 2 - Características das retas concorrentes
- 3 - Quais os tipos de retas concorrentes?
- 4 - Ângulos opostos pelo vértice
- 5 - Classificação das retas
- 6 - Exercícios resolvidos sobre retas concorrentes
Resumo sobre retas concorrentes
-
Duas retas são concorrentes quando têm um único ponto em comum.
-
Quando as duas retas se encontram, são formados quatro ângulos.
-
Duas retas concorrentes podem ser perpendiculares, quando os ângulos formados entre elas são de 90°, e oblíquas, caso contrário.
-
Existem outras posições possíveis para duas retas, além das retas concorrentes, são elas:
-
retas paralelas: não têm nenhum ponto em comum;
Anuncie aqui -
retas coincidentes: têm infinitos pontos em comum.
-
Características das retas concorrentes
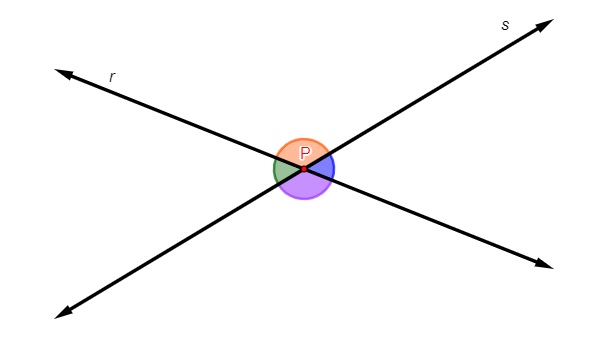
Duas retas distintas pertencentes a um mesmo plano são classificadas como retas concorrentes quando elas têm um único ponto em comum, ou seja, quando se encontram em um único ponto. As principais características de duas retas concorrentes são que elas se encontram em um único ponto P e que, ao se encontrarem nesse ponto, formam-se quatro ângulos entre elas.
Quais os tipos de retas concorrentes?
Quando as retas concorrentes se encontram, de acordo com a medida do ângulo existente entre elas, há duas classificações possíveis: perpendiculares ou oblíquas.
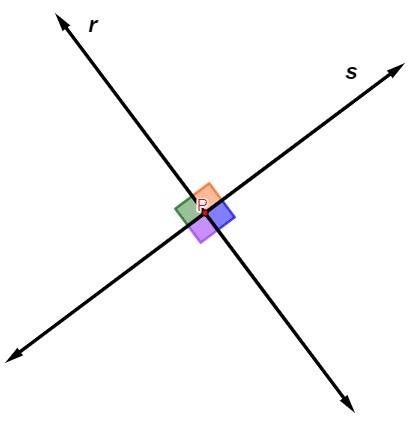
As retas concorrentes são perpendiculares quando formam ângulos retos, ou seja, que medem 90° cada.
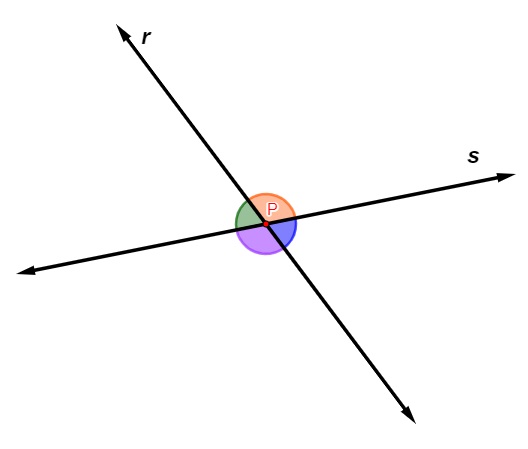
Quando as retas concorrentes não formam ângulo de 90°, elas são oblíquas.
Ângulos opostos pelo vértice
O ponto de encontro entre duas retas concorrentes é chamado de vértice. Sabemos que são formados quatro ângulos e que eles são opostos pelo vértice de dois a dois. Os ângulos opostos pelo vértice são congruentes, ou seja, possuem a mesma medida.
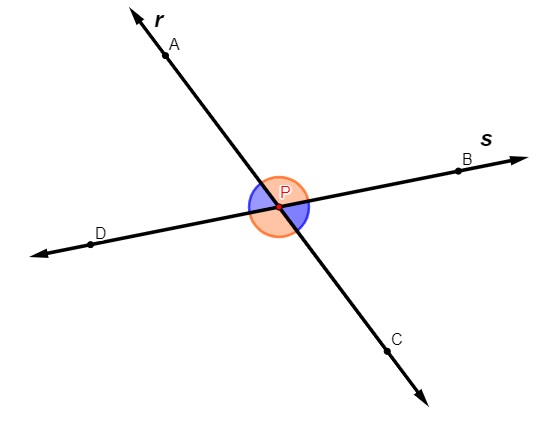
Os ângulos APB e CPD (em laranja) são opostos pelo vértice, logo, eles são congruentes. Os ângulos BPC e APD (em azul) são opostos pelo vértice, logo, eles também são congruentes.
Leia também: Posição relativa entre reta e plano
Classificação das retas
Quando estudamos a posição relativa entre duas retas pertencentes a um mesmo plano, existem três posições possíveis. Além das concorrentes, há as retas coincidentes e as retas paralelas.
Duas retas são classificadas como paralelas quando não possuem nenhum ponto em comum, ou seja, essas retas nunca se encontram.
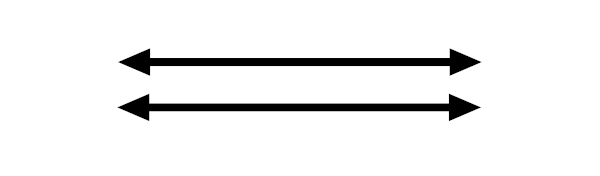
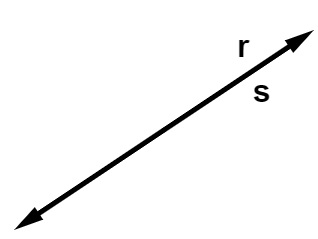
Duas retas são coincidentes quando possuem infinitos pontos em comum.
Exercícios resolvidos sobre retas concorrentes
Questão 1
Durante o projeto de uma construção, um arquiteto fez o desenho de duas retas e afirmou que elas são perpendiculares. Então podemos afirmar que:
A) essas duas retas não têm nenhum ponto em comum.
B) essas duas retas têm um único ponto em comum.
C) essas duas retas têm dois pontos em comum.
D) essas duas retas têm infinitos pontos em comum.
Resolução:
Alternativa B
Duas retas são perpendiculares quando elas se encontram em um único ponto, logo, elas têm um único ponto em comum, ou seja, são concorrentes.
Questão 2
Analisando a imagem a seguir, podemos afirmar que o valor de y – x é:
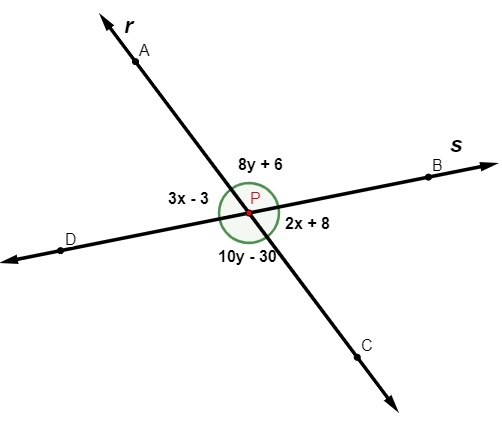
A) 5
B) 7
C) 10
D) 12
E) 19
Resolução:
Alternativa B
Sabemos que ângulos opostos pelo vértice são congruentes, logo, temos que:
3x – 3 = 2x + 8
3x – 2x = 8 + 3
x = 11
Agora, calculando o valor de y, temos que:
10y – 30 = 8y + 6
10y – 8y = 30 + 6
2y = 36
y = 36 : 2
y = 18
Calculando a diferença:
y – x = 18 – 11 = 7
Por Raul Rodrigues de Oliveira
Professor de Matemática