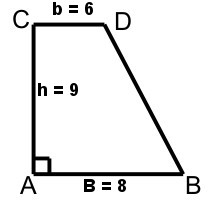
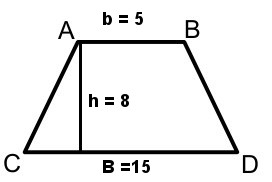
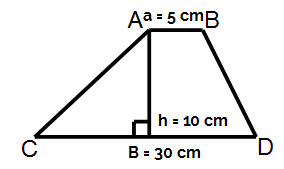
O trapézio é uma figura da geometria plana bastante presente no nosso dia a dia. Trata-se de um polígono que possui quatro lados, sendo dois lados paralelos (conhecidos como base maior e base menor) e dois não paralelos (lados oblíquos). Como todo quadrilátero, ele possui duas diagonais, e a soma dos seus ângulos internos é sempre igual a 360º.
Um trapézio pode ser classificado como trapézio retângulo, quando possui dois ângulos retos; trapézio isósceles, quando os lados não paralelos são congruentes, ou seja, possuem a mesma medida; e trapézio escaleno, quando todos os lados possuem medidas diferentes. O perímetro de um trapézio é calculado pela soma de seus lados, e há fórmulas específicas para calcular a área e a mediana de Euler do trapézio.
Tópicos deste artigo
- 1 - Elementos de um trapézio
- 2 - Classificação do trapézio
- 3 - Propriedades do trapézio
- 4 - Perímetro do trapézio
- 5 - Área do trapézio
- 6 - Base média do trapézio
- 7 - Mediana do trapézio
- 8 - Exercícios resolvidos sobre trapézio
Elementos de um trapézio
Definimos como trapézio todo quadrilátero que possui dois lados paralelos. Os lados paralelos são conhecidos como base maior e base menor. Como todo quadrilátero, possui duas diagonais, e a soma dos ângulos internos é igual a 360º.
Os elementos do trapézio são:
-
Quatro lados;
-
Dois lados paralelos entre si e dois não paralelos;
-
Quatro vértices;
-
Quatro ângulos internos, cuja soma é igual a 360º;
Anuncie aqui -
Duas diagonais.
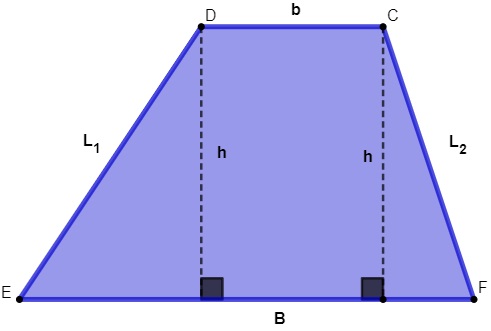
-
C, D, E, F: vértices
-
B: base maior do trapézio
-
b: base menor do trapézio
-
h: altura
-
L1 e L2: lados oblíquos
Anuncie aqui
Leia também: Círculo e circunferências – figuras planas que podem gerar dúvidas
Classificação do trapézio
Existem três possíveis classificações para um trapézio de acordo com o formato que ele possui. Um trapézio pode ser retângulo, isósceles ou escaleno.
-
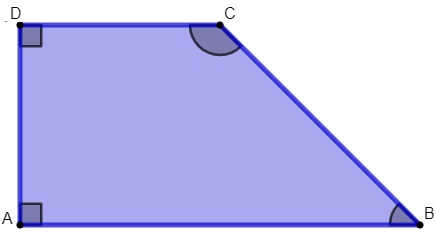
Trapézio retângulo
Possui dois ângulos retos.
-
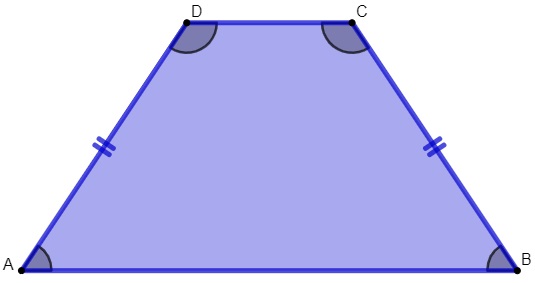
Trapézio isósceles
Possui os lados oblíquos congruentes, ou seja, os lados não paralelos possuem a mesma medida.
-
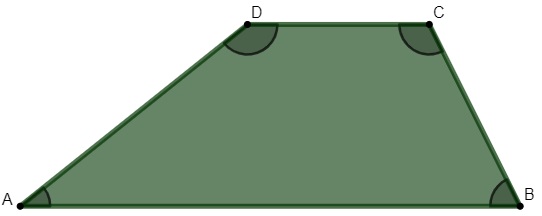
Trapézio escaleno
Possui todos os lados distintos.
Propriedades do trapézio
Como propriedade específica do trapézio, podemos afirmar que os ângulos adjacentes dos lados não paralelos possuem soma igual a 180º.
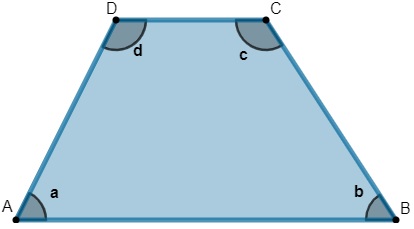
a + d = 180º
b + c = 180º
-
Propriedades específicas para o trapézio isósceles
Existem duas propriedades que são específicas do trapézio isósceles. A primeira delas é que os ângulos da base, assim como os lados não paralelos, são congruentes.
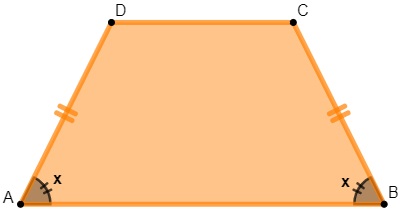
A segunda propriedade do trapézio isósceles é que, ao traçarmos as alturas, formamos dois triângulos congruentes, além de ser possível a aplicação do teorema de Pitágoras nesse triângulo.
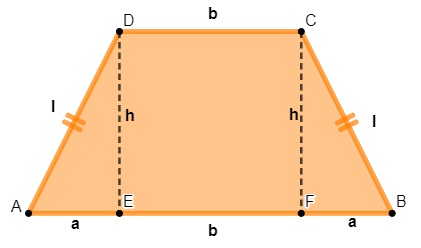
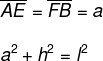
Observação: Existe uma relação na base maior – não é uma propriedade, mas é uma relação importante para a resolução de exercícios – que podemos descrever como:
B = b + 2a
Veja também: Triângulo equilátero – propriedades e particularidades
Perímetro do trapézio
O perímetro de um trapézio qualquer é calculado pela soma de todos os lados.
P = B + b + L1 + L2
-
Exemplo
Qual será a quantidade de arame, em metros, para dar cinco voltas no terreno que possui o formato do trapézio escaleno abaixo:
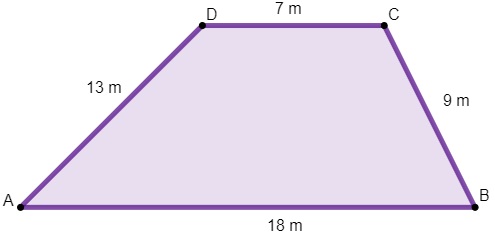
Resolução
P = 18 + 13 + 7 + 9 = 47 metros.
Como serão dadas cinco voltas, então 5P = 5 . 47 = 235 metros de fio.
Área do trapézio
Para calcular a área do trapézio, há uma fórmula específica, que depende do valor das bases e da altura.
![]()
-
Exemplo
Em uma vidraçaria, os vidros são produzidos sob encomenda, custando R$ 96,00 o m². Para construir o vidro que ficará em uma mesa no formato de um trapézio (base maior mede 1,3 m; base menor mede 0,7 m; altura mede 1 m.), o valor gasto no vidro será de?
Resolução
B = 1,3
b = 0,7
h =1
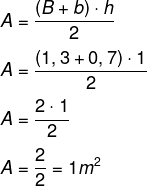
Como a mesa tem exatamente 1 m², serão gastos R$ 96,00.
Base média do trapézio
A base média do trapézio é o segmento paralelo à base maior e à base menor que une os pontos médios dos lados oblíquos.
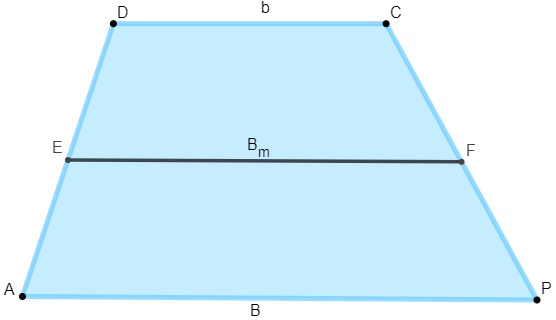
E e F são pontos médios dos seus respectivos lados, e o segmento formado ao ligar esses pontos é a base média. O comprimento da base média é calculado pela média aritmética entre a base maior e base menor:
![]()
Mediana do trapézio
Conhecida como mediana de Euler do trapézio (Me), trata-se do segmento de reta formado pela ligação entre os pontos médios das duas diagonais do trapézio.
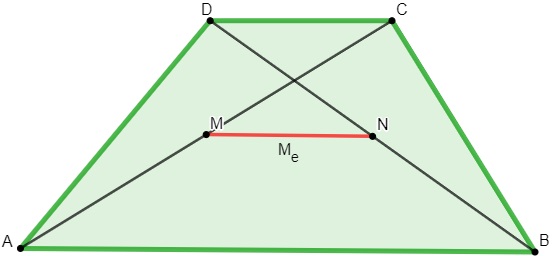
Para calcular o comprimento da mediana de Euler, a fórmula é a seguinte:
![]()
-
Exemplo 1
Encontre o comprimento da mediana do trapézio cujas bases medem 7 cm e 10 cm.
Resolução
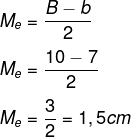
-
Exemplo 2
Calcule o valor da base maior e da base menor do trapézio abaixo sabendo que M e N são pontos médios das diagonais.
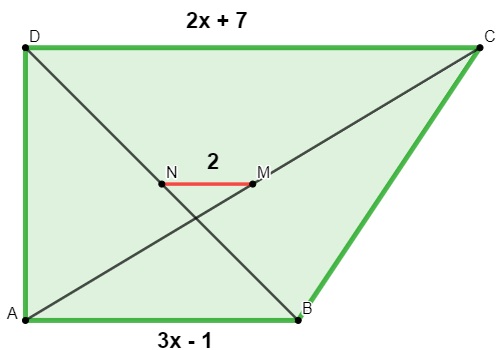
Resolução
Sabemos que B = 2x + 7, b = 3x -1 e Me = 2, logo:
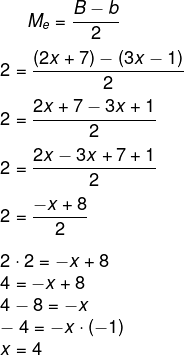
Como x = 4, então é possível encontrar a base maior e a base menor substituindo x.
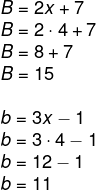
Acesse também: Ponto, reta, plano e espaço: conceitos básicos da geometria
Exercícios resolvidos sobre trapézio
Questão 1 - Sabendo que um trapézio possui base maior igual a 15 e base menor igual a 7, o valor da diferença entre o comprimento da sua base média e a sua mediana de Euler é igual a?
a) 11
b) 4
c) 6
d) 7
e) 8
Resolução
1º passo: calcular o comprimento da base média.
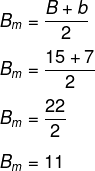
2º passo: calcular o comprimento da mediana de Euler.
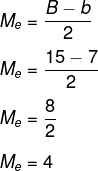
3º passo: calcular a diferença entre Bm e Me.
11 – 4 = 7
Logo, a alternativa correta é a letra “d”.
Questão 2 - As bases de um trapézio isósceles medem 6 cm e 14 cm, e um lado oblíquo mede 5 cm, então, pode-se afirmar que a área desse trapézio, em cm², é:
a) 28
b) 30
c) 32
d) 34
e) 40
Resolução
Para calcularmos a área desse trapézio, precisamos encontrar a altura. Para isso, faremos o desenho de um trapézio isósceles com as informações dadas:
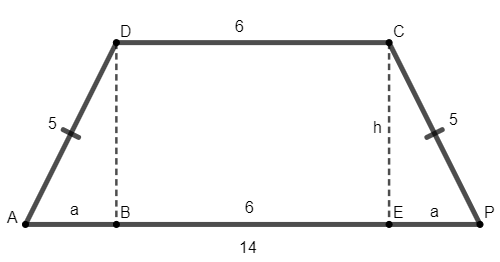
Como para calcular a área precisamos do valor das duas bases e do valor de h, que ainda não conhecemos, vamos encontrar o valor de a para aplicar o teorema de Pitágoras no triângulo CEP.
Sabemos que:
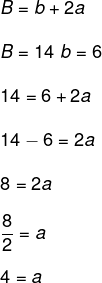
Encontrando o valor de a, é possível calcular o valor de h pelo teorema de Pitágoras.
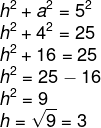
Conhecendo o valor de h, é possível calcular a área do trapézio:
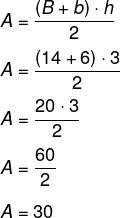
Logo, a alternativa correta é a letra “b”.



.jpg)