Classificação de triângulos

A classificação de triângulos é bastante útil para o desenvolvimento do estudo e das propriedades específicas dessa figura geométrica, que tem grande importância na geometria plana. Existem duas maneiras de classificar triângulos. Uma delas leva em consideração os ângulos e, nesse caso, um triângulo pode ser acutângulo, quando possui todos os seus ângulos internos agudos; retângulo, quando um dos seus ângulos internos é reto; ou obtusângulo, quando um de seus ângulos internos é obtuso.

A outra classificação baseia-se na comparação entre os lados. Nesse caso, um triângulo pode ser escaleno, quando todos os lados possuem medidas diferentes; isósceles, quando existem dois lados que possuem mesma medida; ou equilátero, quando todos os lados são congruentes.

Leia também: Paralelogramo – polígono que possui lados opostos paralelos

Tópicos deste artigo

• 1 - Propriedades dos triângulos
• 2 - Classificação dos triângulos
  • Classificação de triângulos quanto aos ângulos
  • Classificação quanto ao lado
• 3 - Exercícios resolvidos

Propriedades dos triângulos

Um triângulo é um polígono de três lados, três vértices e três ângulos. Normalmente os vértices são representados por letras maiúsculas do nosso alfabeto, e a medida dos lados é representada por letras minúsculas. Já os ângulos são representados por letras do alfabeto grego.

Existem elementos e propriedades comuns a todos os triângulos, que são:

• O triângulo não possui diagonal.
• O triângulo possui três ângulos externos cuja soma é sempre igual a 360º.
• A soma dos ângulos internos (S_i) é sempre igual a 180º.
• A soma de dois lados quaisquer é sempre menor que o terceiro lado.
• Todo triângulo possui altura, mediana, mediatriz e bissetriz.
• Todo triângulo possui pontos notáveis importantes: baricentro (encontro das três medianas), circuncentro (encontro das três mediatrizes), incentro (encontro das três bissetrizes) e ortocentro (encontro das três alturas).
• A área de um triângulo qualquer pode ser calculada pela fórmula:

A: área

b: base

h: altura

Classificação dos triângulos

Existem duas formas de classificar os triângulos, que são independentes entre si. Uma delas leva em consideração os ângulos – nesse caso, um triângulo pode ser obtusângulo, acutângulo ou retângulo. Já a outra maneira de classificar faz a comparação entre o comprimento de cada um dos lados, com isso um triângulo pode ser escaleno, equilátero ou isósceles.

• Classificação de triângulos quanto aos ângulos

Ao analisar os ângulos internos do triângulo, chegamos a três casos:

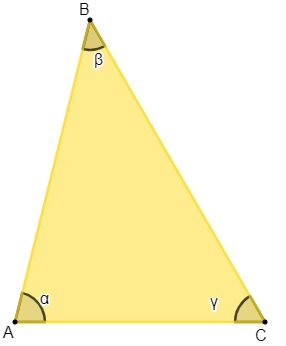
• Triângulo acutângulo

Um triângulo é conhecido como acutângulo quando os seus três ângulos são agudos, ou seja, menores que 90º.

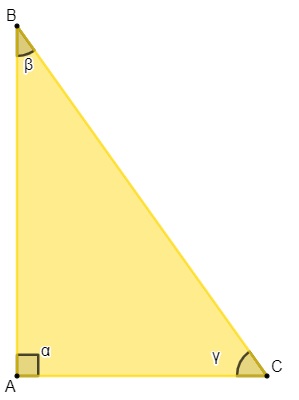
• Triângulo retângulo

Um triângulo é retângulo quando um de seus ângulos é reto, ou seja, igual a 90º. Como a soma dos três ângulos é sempre igual a 180º, os demais ângulos são necessariamente agudos.

O triângulo retângulo é muito importante para a Matemática, pois, com base nele, são desenvolvidas relações de grande importância, como as relações trigonométricas no triângulo retângulo e o teorema de Pitágoras. Para saber mais informações sobre esse tipo de triângulo, acesse o nosso texto: triângulo retângulo.

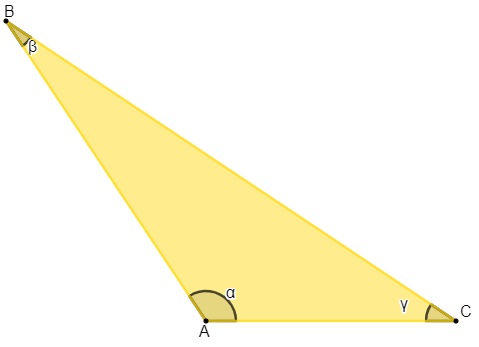
• Triângulo obtusângulo

Um triângulo é obtusângulo quando um de seus ângulos é obtuso, ou seja, maior que 90º. Os demais ângulos são necessariamente agudos.

Veja também: Semelhança de triângulos – comparação entre lados proporcionais e ângulos congruentes

• Classificação quanto ao lado

Analisando os lados do triângulo, podemos também separar três casos:

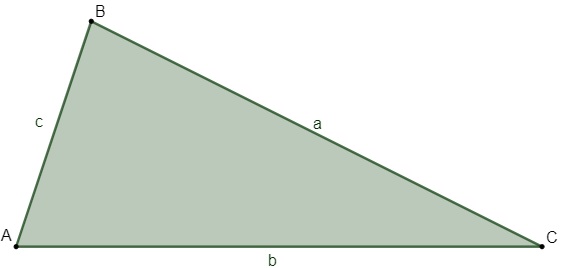
• Triângulo escaleno

O triângulo é escaleno quando as medidas dos lados são todas diferentes.

• Triângulo isósceles

O triângulo é isósceles quando possui pelo menos dois lados congruentes, ou seja, com a mesma medida. Devido a essa particularidade, o triângulo isósceles possui propriedades específicas, que não são válidas para triângulos escalenos.

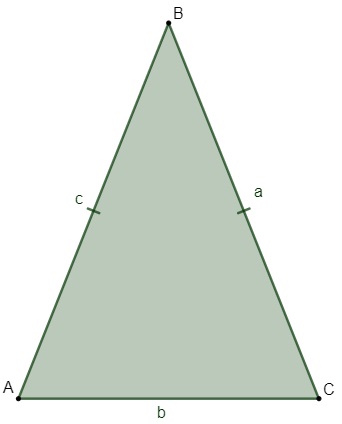
As propriedades específicas do triângulo isósceles são duas, uma em relação ao ângulo e outra em relação à altura.

• Em triângulos isósceles, os ângulos da base são sempre iguais (tratamos como base o lado que possui medida diferente dos demais lados).

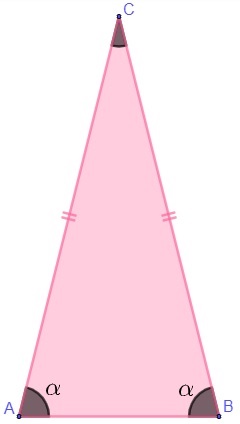
• Ao traçar a altura h do triângulo isósceles, ela divide a base em duas partes iguais.

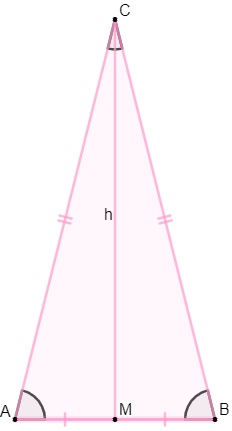
Note que os segmentos AM e BM são congruentes, o que significa que M é o ponto médio da base desse triângulo.

• Triângulo equilátero

O triângulo é equilátero quando possui os três lados com as mesmas medidas. Como consequência, os três ângulos também possuem a mesma medida, que é de 60º. Existem fórmulas específicas para o cálculo de área e de altura desse triângulo, a s quais são deduzidas a partir dos três lados congruentes.

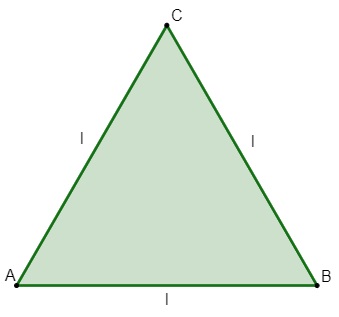
No triângulo equilátero, as propriedades do triângulo isósceles também são válidas, afinal, ele possui mais de dois lados iguais. Além disso, conhecendo o lado do triângulo equilátero, podemos encontrar a altura e a sua área pelas fórmulas a seguir:

• Altura do triângulo equilátero

• Área do triângulo equilátero

Acesse também: Trapézio – polígono de quatro lados com dois deles paralelos

Exercícios resolvidos

Questão 1 - Das sentenças abaixo, assinale a que é verdadeira.

A) Um triângulo equilátero pode ser retângulo.

B) Todo triângulo retângulo é escaleno.

C) Todo triângulo equilátero é acutângulo.

D) Todo triângulo obtuso é isósceles.

E) Todo triângulo isósceles é acutângulo.

Resolução

Alternativa C.

Analisando as alternativas, temos que:

A) Um triângulo equilátero possui todos os lados iguais e, consequentemente, todos os ângulos, que medem 60º, o que torna impossível um triângulo equilátero ser retângulo.

B) Pelo argumento da alternativa anterior, sabemos que um triângulo retângulo não pode ser equilátero, resta saber se ele pode ser isósceles. Sabendo que ele possui um ângulo de 90º, se os outros dois ângulos forem de 45º cada, teremos um triângulo retângulo isósceles, logo nem todo triângulo retângulo é escaleno.

C) Sabendo que os ângulos internos de um triângulo equilátero valem 60º, então é verdade que ele é acutângulo.

D) Um triângulo obtuso pode ser isósceles (por exemplo, se os seus ângulos medirem 100º, 40º e 40º) e escaleno também (por exemplo, se apresentar ângulos de 120º, 20º e 40º). Existem várias outras possibilidades para que ele seja escaleno, o que torna a afirmativa falsa.

E) Pela explicação da letra D, sabemos que um triângulo isósceles pode ser obtuso e, pela explicação da letra B, sabemos que ele pode ser retângulo, o que torna essa sentença falsa.

Questão 2 - Assinale a alternativa correta sobre a classificação dos triângulos.

A) Triângulo equilátero é aquele que possui todos os ângulos medindo 90º.

B) Triângulo isósceles é aquele que possui todos os lados diferentes.

C) Triângulo acutângulo é aquele que possui exatamente um ângulo agudo.

D) Triângulo obtusângulo é aquele que possui um ângulo obtuso.

E) Triângulo retângulo é aquele que possui todos os seus ângulos retos.

Resolução

Alternativa D.

a) O triângulo equilátero possui todos os ângulos iguais a 60º, e não a 90º.

b) O triângulo isósceles é aquele que possui pelo menos dois lados iguais.

c) O triângulo acutângulo possui todos os ângulos agudos, e não somente um.

d) Essa alternativa é a verdadeira, pois essa é a definição de um triângulo obtusângulo.

e) O triângulo retângulo possui somente um ângulo reto.

 

Raul Rodrigues de Oliveira
Professor de Matemática