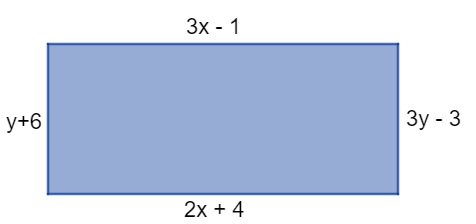
O retângulo é um polígono estudado na geometria plana. Como ele tem quatro lados, é classificado como um quadrilátero, e recebe o nome retângulo pelo fato de possuir os quatro ângulos retos, ou seja, com medida de 90º.
O retângulo possui propriedades herdadas por ser um quadrilátero e também propriedades específicas. Para saber a área de um retângulo, calculamos o produto da base pela altura; já o seu perímetro é igual a soma de todos os seus lados. O retângulo possui duas diagonais, e uma das suas propriedades é que elas são congruentes. Para encontrar o comprimento da diagonal, aplicamos o teorema de Pitágoras.
Leia também: Círculo e circunferência – formas geométricas com muitas particularidades
Tópicos deste artigo
- 1 - Elementos do retângulo
- 2 - Propriedades do retângulo
- 3 - Área do retângulo
- 4 - Perímetro do retângulo
- 5 - Diagonal do retângulo
- 6 - Trapézio retângulo
- 7 - Triângulo retângulo
- 8 - Retângulo áureo
- 9 - Exercícios resolvidos
Elementos do retângulo

O retângulo é um polígono com quatro lados e cujos ângulos são retos. Essa forma geométrica é bastante comum no cotidiano, como planta baixa de residências, faces de caixas, portas, entre outros objetos que têm essa forma.
O retângulo possui quatro lados, quatro vértices, quatro ângulos internos, e é possível traçar duas diagonais.
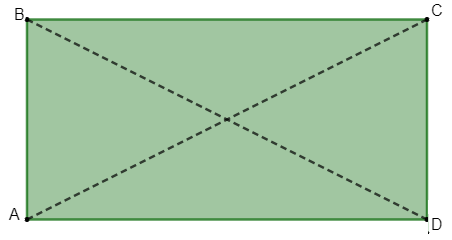
- A, B, C e D são os vértices do retângulo.
- AB, AD, BC e CD são os lados do retângulo.
- AC e BD são diagonais.
Propriedades do retângulo
O retângulo possui propriedades importantes, herdadas pelo fato de ser um paralelogramo, ou seja, ter os lados paralelos. Temos que:
- Os lados opostos são paralelos e congruentes.
- Dois ângulos internos de um mesmo lado são sempre suplementares, ou seja, somam 180º.
- Todos os ângulos medem 90º, logo, assim como nos demais paralelogramos, os ângulos opostos são congruentes e os ângulos adjacentes são sempre suplementares.
- As diagonais são sempre congruentes.
- O ponto de encontro das diagonais é também o ponto médio de cada uma das diagonais.
Veja também: Ponto, reta, plano e espaço: conceitos básicos da geometria
Área do retângulo
O cálculo de área do retângulo é bastante recorrente para encontrar a área de outros polígonos. Por ter uma fórmula bem simples para o cálculo de área, é comum dividir um polígono em vários retângulos para calcular a sua área, e, por isso, a área do retângulo é uma das mais importantes entre os polígonos.
Para saber a área do retângulo, calculamos a multiplicação entre a base e a altura:
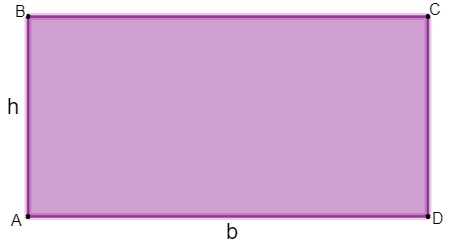
A = b × h
Perímetro do retângulo
O perímetro do retângulo, assim como nos demais polígonos, é igual à soma de todos os seus lados.
Calcular o perímetro é encontrar o comprimento do contorno do polígono. No retângulo, como sabemos, os lados são congruentes dois a dois, é possível então calcular o perímetro do retângulo por meio da fórmula:
P = 2(b + h)
Exemplo:
Calcule o perímetro e a área do retângulo que possui lados medindo 5 cm e 7 cm.
Como a adição é comutativa, ou seja, a ordem das parcelas não altera a soma, podemos escolher b = 5 e h = 7.
P = 2(5 + 7)
P = 2 · 12
P = 24 cm
A = b × h
A = 5 × 7
A = 35 cm²
Diagonal do retângulo
Quando traçamos qualquer uma das diagonais do retângulo, estamos dividindo-o em dois triângulos retângulos, sendo assim, é possível encontrar o comprimento da diagonal do retângulo pelo teorema de Pitágoras.
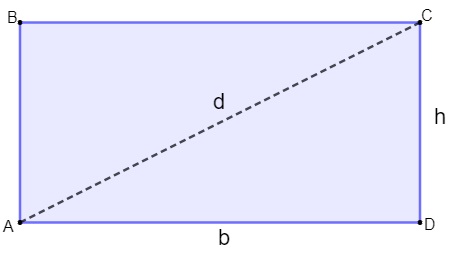
d² = b² + h²
Trapézio retângulo
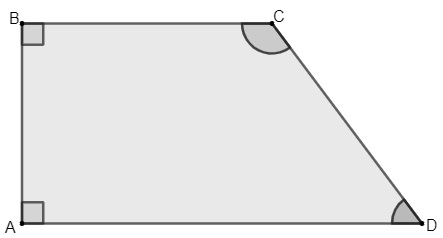
O trapézio, assim como o retângulo, é um quadrilátero. A diferença é que, no trapézio, somente dois lados são paralelos, e os outros dois não. Quando um trapézio possui dois de seus ângulos retos, ele é conhecido como trapézio retângulo.
Triângulo retângulo
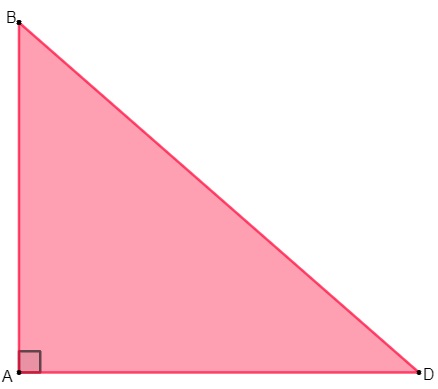
O triângulo retângulo é um polígono de grande importância para a matemática. Estudado a fundo, é nele que se desenvolve grande parte dos estudos da trigonometria, e também existe a importante relação pitagórica entre os seus lados. Retângulos, quadrados e losangos sempre podem ser divididos, por suas diagonais, em triângulos retângulos. O triângulo é retângulo quando possui um dos seus ângulos retos, ou seja, igual a 90º.
Acesse também: Quais são os critérios para classificar um triângulo?
Retângulo áureo
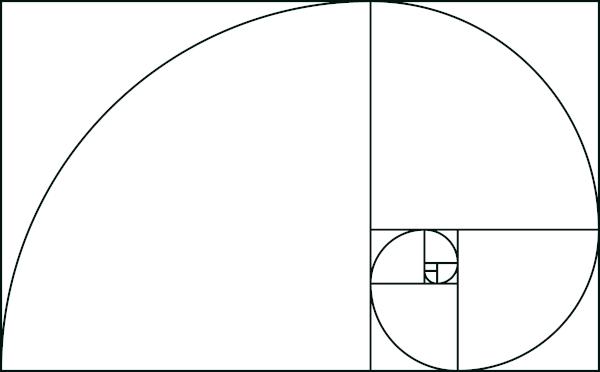
O retângulo áureo, conhecido também como retângulo de ouro, é bastante admirado pelos matemáticos, arquitetos e artistas. Ele é assim conhecido por ter a proporção áurea. Perceber a existência da proporção áurea em quadros e construções artísticas é bastante comum. Muitas vezes essa proporção é relacionada com objetos considerados belos, pela harmônia que ela preserva. Quando dividimos o retângulo, para que ele seja considerado áureo, temos que:
Exercícios resolvidos
Questão 1 – (IFG 2019) Considere que o tamanho de uma televisão, dado em polegadas, corresponde ao comprimento da sua diagonal e que, no caso de televisores de tamanho normal, a largura e a altura seguem, ordenadamente, a relação 4:3. Observe a figura abaixo e considere que 1 polegada é aproximadamente 2,5 cm
Com relação a uma televisão plana de 40 polegadas, é correto afirmar que sua largura e sua altura são, respectivamente:

A) 60 cm e 45 cm
B) 80 cm e 60 cm
C) 64 cm e 48 cm
D) 68 cm e 51 cm
Resolução
Alternativa B. Ao traçar a diagonal da figura, sabemos que é possível formar um triângulo retângulo. Como os lados têm proporção 3 para 4, então temos que a altura mede 3x, e o comprimento, 4x. Aplicando o teorema de Pitágoras, temos que:
(3x)² + (4x²) = 40²
9x² + 16x² = 1600
25x² = 1600
x² = 1600/25
x² = 64
x = √64
x = 8
Sabendo o valor de x, então um lado mede, em polegadas:
3x → 3 · 8 = 24”
4x → 4 · 8 = 32”
Como 1 polegada equivale a 2,5 cm, então temos que:
24 · 2,5 = 60 cm
32 · 2,5 = 80 cm
Questão 2 – Em um retângulo, um lado é igual a 2/3 do outro lado. Sabendo que seu perímetro é igual a 120 cm, a área desse retângulo é:
A) 326 cm²
B) 532 cm²
C) 432 cm²
D) 864 cm²
Resolução
Alternativa D
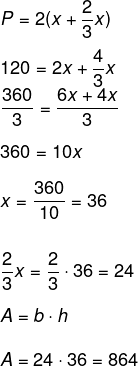
Por Raul Rodrigues de Oliveira
Professor de Matemática