O triângulo é um polígono que possui três lados. Ele é o polígono mais simples, pois possui o menor número de lados. Os principais elementos dessa figura geométrica são os seus três lados e os três ângulos.
Para calcular o perímetro de um triângulo, basta somar os seus lados. Já a área é calculada pelo produto entre o comprimento da base e da altura dividido por dois. A propriedade mais importante de um triângulo é que a soma dos seus ângulos internos é sempre igual a 180º.
Leia também: Quais são os pontos notáveis de um triângulo?
Tópicos deste artigo
- 1 - Resumo sobre triângulo
- 2 - Elementos de um triângulo
- 3 - Propriedades de um triângulo
- 4 - Classificação do triângulo
- 5 - Condição de existência do triângulo
- 6 - Área do triângulo
- 7 - Perímetro do triângulo
- 8 - Exercícios resolvidos sobre triângulos
Resumo sobre triângulo
-
O triângulo é um polígono de 3 lados e 3 ângulos.
-
A soma dos ângulos internos de um triângulo é sempre igual a 180º.
-
Um triângulo pode ser classificado com relação aos seus lados em:
-
equilátero: todos os lados congruentes;
-
isósceles: dois lados congruentes;
-
escaleno: todos os lados com medidas distintas.
-
-
Um triângulo pode ser classificado quanto aos ângulos em:
-
retângulo: possui um ângulo reto;
-
acutângulo: possui todos os ângulos agudos;
-
obtusângulo: possui um ângulo obtuso.
-
Elementos de um triângulo
Os principais elementos de um triângulo são os lados e os seus ângulos internos. Vale dizer que ele é o único polígono que não possui diagonal.
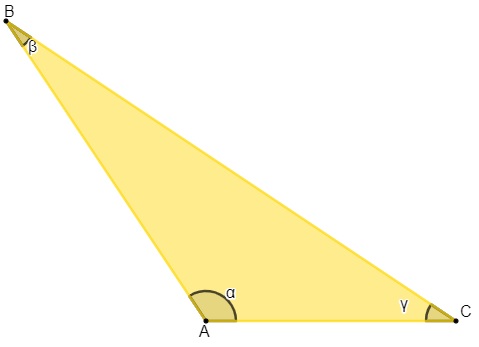
-
Os lados são os segmentos de reta AB, AC e BC.
-
Os ângulos internos são os ângulos α, ꞵ e γ.
Propriedades de um triângulo
As propriedades a seguir são válidas para todo triângulo.
-
A soma dos ângulos internos é sempre igual a 180°.
-
A soma dos ângulos externos é sempre igual a 360°.
-
O menor lado é sempre oposto ao menor ângulo interno do triângulo.
-
O maior lado é sempre oposto ao maior ângulo interno do triângulo.
Veja também: Os 4 erros mais cometidos na trigonometria básica
Classificação do triângulo
Há duas maneiras distintas de classificar um triângulo: uma delas leva em consideração os lados, e a outra, os ângulos.
→ Classificação dos triângulos quanto aos lados
Quanto aos lados, há três casos possíveis: o triângulo pode ser equilátero, isósceles ou escaleno.
-
Triângulo equilátero
O triângulo é classificado como equilátero quando as medidas dos seus lados são todas congruentes e, consequentemente, os ângulos também.
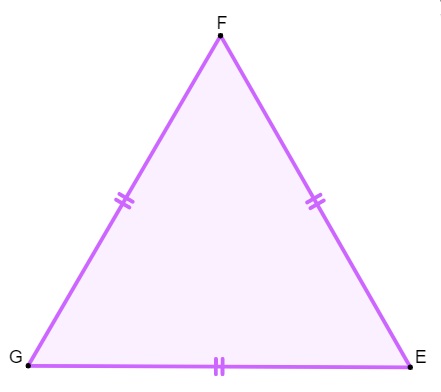
-
Triângulos isósceles
Um triângulo é isósceles quando possui exatamente dois lados congruentes.
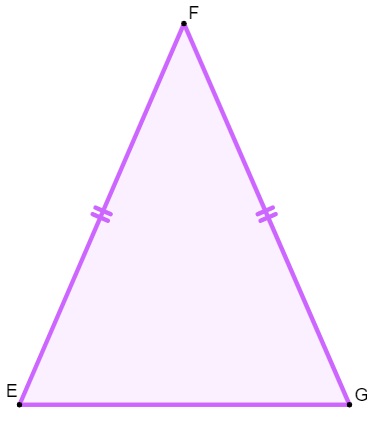
-
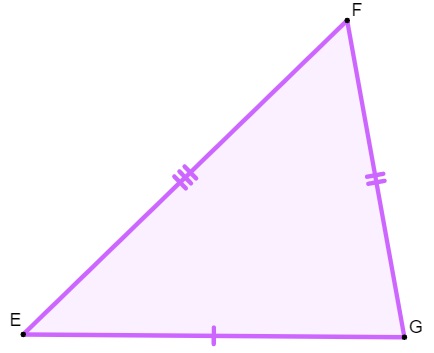
Triângulo escaleno
Um triângulo é classificado como escaleno quando ele possui todos os lados com medidas distintas.
→ Classificação dos triângulos quanto aos ângulos
Quando analisamos os ângulos do triângulo, há também três casos: o triângulo acutângulo, o triângulo retângulo e o triângulo obtusângulo.
-
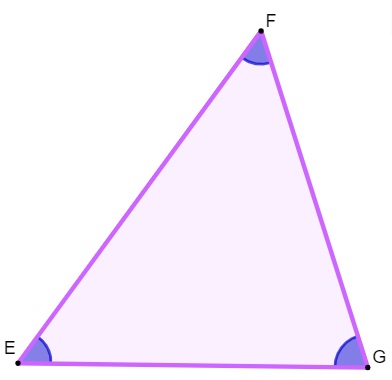
Triângulo acutângulo
O triângulo é classificado como acutângulo quando ele possui todos os ângulos agudos.
-
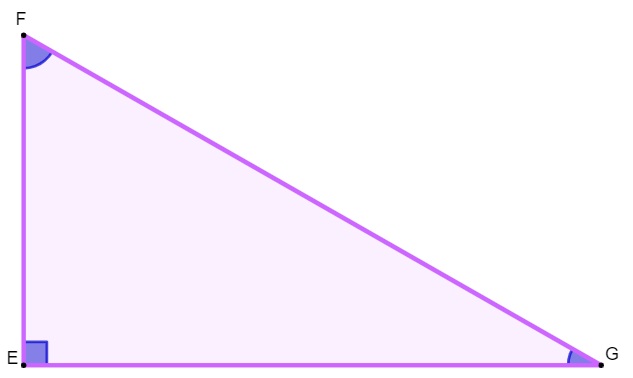
Triângulo retângulo
O triângulo é retângulo quando ele possui um ângulo reto, ou seja, um ângulo de 90°.
-
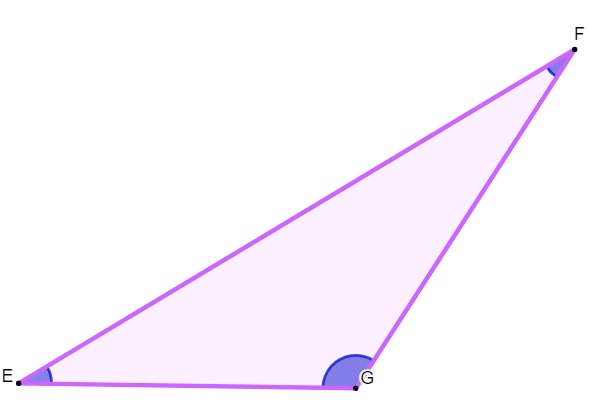
Triângulo obtusângulo
O triângulo é classificado como obtusângulo quando ele possui um ângulo obtuso.
→ Videoaula sobre classificação dos triângulos
Condição de existência do triângulo
Dados três segmentos de reta, nem sempre eles podem formar um triângulo. Para que os três segmentos formem um triângulo, existe o que conhecemos como condição de existência, que é a seguinte: a soma de dois lados é sempre maior que o terceiro lado.
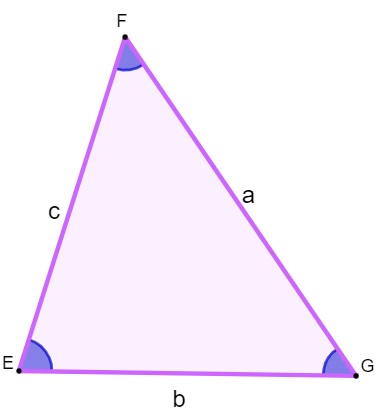
Em um triângulo, segundo a condição de existência, temos que:
a + b > c
b + c > a
a + c > b
Veja também: Quais são os ângulos notáveis?
Área do triângulo
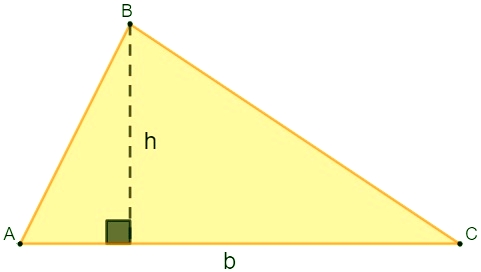
A área do triângulo é calculada multiplicando a base pela altura e dividindo por 2. Então, dado o triângulo de altura h e base b, como o da imagem a seguir, para calcular a área, utilizamos a seguinte fórmula:
![]()
Exemplo:
Dado um triângulo com base medindo 12 cm e altura igual a 8 cm, calcule a sua área.
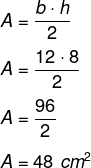
-
Videoaula sobre área do triângulo
Perímetro do triângulo
O perímetro de um triângulo, assim como dos demais polígonos, é calculado pela soma de todos os lados.
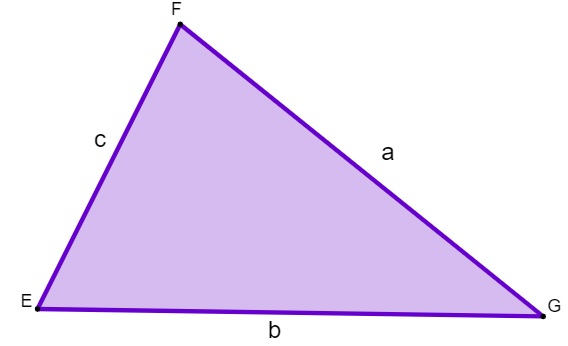
P = a + b + c
Exercícios resolvidos sobre triângulos
1. Deseja-se cercar o terreno a seguir com uma cerca contendo 4 fios de arame.
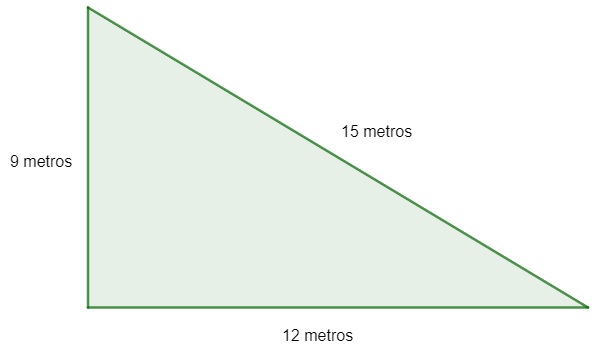
A quantidade mínima necessária de arame para construir essa cerca é de:
A) 36.
B) 54.
C) 72.
D) 108.
E) 144.
Resolução
Alternativa E.
Para encontrar a quantidade de arame necessária para cercar o terreno, devemos determinar o perímetro e, depois, multiplicar por 4.
P = 15 + 9 + 12
P = 36
Como serão dadas 4 voltas, então 36 · 4 = 144 m.
2. Sobre os triângulos, julgue as afirmativas a seguir:
I → O triângulo possui 3 lados, 3 ângulos e 1 diagonal.
II → Todo triângulo equilátero é acutângulo.
III → Em um triângulo retângulo, a soma dos ângulos não retângulos é sempre igual a 90º.
Marque a alternativa correta:
A) Somente a afirmativa I é incorreta.
B) Somente a afirmativa II é incorreta.
C) Somente a afirmativa III é incorreta.
D) Todas as afirmativas são incorretas.
E) Todas as afirmativas são corretas.
Resolução
Alternativa A.
I → Falsa. O triângulo é um polígono que não possui diagonal.
II → Verdadeira. Um triângulo equilátero possui todos os ângulos congruentes. Como a soma dos ângulos internos de um triângulo é igual a 180º, sabemos que 180 : 3 = 60°.
III → Verdadeira. Se um triângulo é retângulo, ele possui um ângulo igual a 90º. Como a soma dos três ângulos internos é 180º, sabemos que 180 – 90 = 90º, então a soma dos dois ângulos restantes é, de fato, igual a 90º.
Por Raul Rodrigues de Oliveira
Professor de Matemática