Polígonos convexos

Polígonos são figuras geométricas planas compostas apenas por uma linha fechada, que, por sua vez, é formada apenas por segmentos de reta. Um polígono é considerado convexo ou não convexo de acordo com o formato dessa linha. Se existir algum vértice voltado para o interior do polígono, ele não será convexo, caso contrário, será.

Polígonos convexos e não convexos

Um polígono é convexo quando todos os pontos de um segmento de reta que possui as extremidades no interior do polígono também estão dentro dele. Sendo assim, se for possível encontrar pelo menos um segmento de reta que possui as extremidades dentro do polígono e, ao mesmo tempo, um ponto fora dele, esse polígono não será convexo.

A imagem a seguir, à esquerda, mostra como são os polígonos convexos e, à direita, como encontrar retas que estão fora do polígono, mesmo com suas extremidades no interior dele.

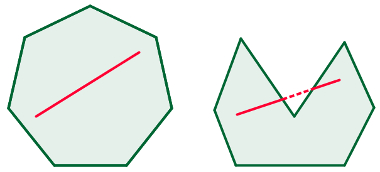
Exemplo de polígono convexo, à esquerda, e não convexo, à direita

Elementos de um polígono convexo

Um polígono convexo qualquer possui os seguintes elementos

• Lados: segmentos de reta que compõem a linha usada para definir os polígonos;

• Vértices: pontos de encontro entre os lados de um polígono;

• Diagonais: segmentos de reta que ligam dois vértices não consecutivos de um polígono;

• Ângulos internos: ângulo entre dois segmentos de reta adjacentes no interior do polígono;

• Ângulos externos: ângulo entre um lado e o prolongamento do lado adjacente a ele.

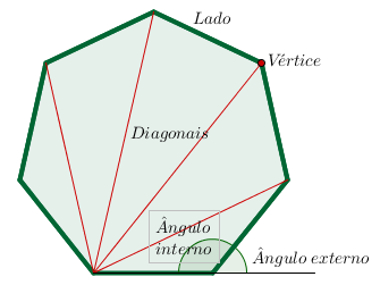
Propriedades de um polígono convexo

• Em qualquer polígono convexo, o número de lados, de ângulos (internos ou externos) e de vértices é igual;

• Em um polígono convexos a soma das medidas dos ângulos internos é dada pela seguinte expressão:

S = (n – 2)180

*n é o número de lados do polígono, e S é o resultado da soma dos ângulos internos.

• Em um polígono regular, a soma das medidas dos ângulos externos sempre é igual a 360°.

Por Luiz Paulo Moreira
Graduado em Matemática