Ponto, reta, plano e espaço são as noções primitivas da Geometria. Esses objetos não possuem definição, mas precisam existir para dar base para as definições geométricas. Embora não seja possível definir esses objetos, é possível discutir suas características, propriedades e suas utilidades para a Geometria.
Ponto
O ponto não possui forma nem dimensão. Isso significa que o ponto é um objeto adimensional. Um dos usos mais importantes do ponto refere-se à localização geográfica. Os pontos são os objetos que melhor representam as localizações porque oferecem precisão. Se, no lugar de ponto, usássemos um quadrado, em que lugar do quadrado estaria a localização precisamente?
Reta
As retas são conjuntos de pontos que não fazem curvas. Elas são infinitas para as duas direções. Como esses pontos não estão no mesmo lugar, é possível medir a distância entre eles. Entretanto, como os pontos continuam não tendo dimensão ou forma, não é possível medir sua largura. Sendo assim, dizemos que a reta possui apenas uma dimensão ou que é unidimensional.
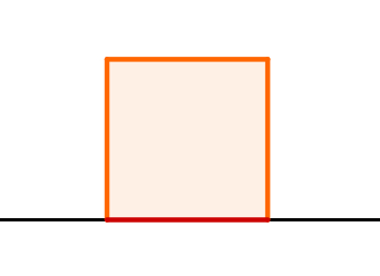
A figura a seguir mostra a tentativa de desenhar um quadrado sobre uma reta. Note que a maior parte do quadrado “não cabe” na reta. Por essa razão, é necessário definir um novo local onde ele possa ser desenhado.
Plano
O plano é um conjunto de retas alinhadas e, portanto, também é um conjunto de pontos. O objeto formado por esse alinhamento de retas é uma superfície plana que não faz curva e infinita para todas as direções.
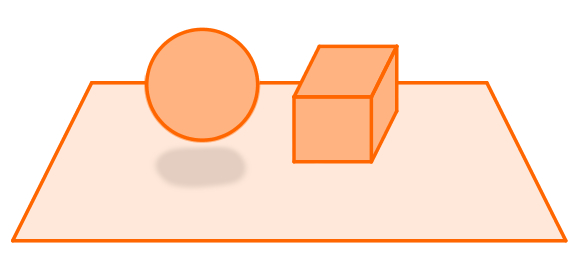
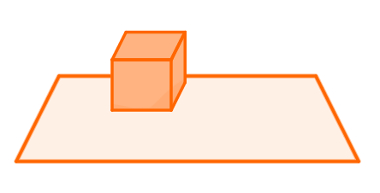
Em um plano, é possível desenhar figuras que, além de comprimento, possuem largura. A figura abaixo mostra um cubo sobre um plano. Note que a base do cubo, que é um quadrado e possui duas dimensões, encaixa-se perfeitamente no plano. Todavia, a profundidade desse sólido não é contemplada.
Espaço
O espaço é o local onde toda a Geometria conhecida até o Ensino Médio acontece. É formado pelo alinhamento de planos, que são colocados lado a lado até preencher todo o espaço. Ele é infinito para todas as direções e contém todas as figuras e formas geométricas planas e tridimensionais.
Como é formado por planos, o espaço envolve a terceira dimensão, necessária para conter todo o cubo da figura anterior. É na terceira dimensão que são construídas figuras que possuem largura, comprimento e profundidade.
Por Luiz Paulo Moreira
Graduado em Matemática
Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:
SILVA, Luiz Paulo Moreira. "Ponto, reta, plano e espaço"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/ponto-reta-plano-espaco.htm. Acesso em 08 de abril de 2020.
A respeito das características do ponto, em Geometria, assinale a alternativa correta:
a) O ponto pode ser definido como a menor unidade geométrica e é usado para definir outras figuras, como retas e planos.
b) O ponto não pode ser definido, mas algumas de suas características podem ser usadas para diferenciá-lo de outras figuras. Por exemplo, o fato de possuir apenas uma dimensão garante que não haja medidas possíveis nos pontos.
c) O ponto pode ser definido como o menor espaço entre duas figuras geométricas.
d) O ponto não pode ser definido e não possui dimensão nem formato, o que garante a precisão de seu uso nas localizações geográficas.
e) O ponto é o único ente geométrico que não pode ser definido.
Sobre a formação, as características e o uso das retas, assinale a alternativa correta.
a) As retas são noções primitivas da Geometria que não possuem definição, mas que apresentam uma única dimensão. Assim, elas permitem que sejam feitas medidas de comprimento ou largura a partir delas.
b) As retas podem ser definidas como a distância entre dois pontos.
c) As retas podem ser definidas como figuras geométricas que não fazem curva.
d) O número de dimensões que as retas possuem possibilita a construção de qualquer figura geométrica sobre elas, desde que essa figura seja feita com base em lados retos. Por exemplo, é possível construir um quadrado sobre uma reta.
e) Segmentos de reta são conjuntos de pontos que possuem início, mas não possuem fim.
Mais Questões
