Relações métricas no triângulo equilátero inscrito

As relações métricas no triângulo equilátero inscrito são expressões que podem ser usadas para calcular algumas das medidas dessa figura por meio apenas da medida do raio da circunferência.

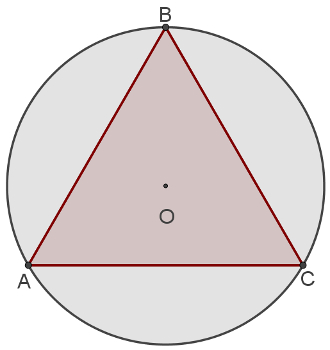
Dizemos que um polígono está inscrito em uma circunferência quando todos os seus vértices pertencem a ela. Um triângulo equilátero é aquele que possui todos os lados congruentes. Como consequência disso, todos os ângulos dele também são congruentes e medem 60°.

A partir dessas informações, observe as relações métricas no triângulo equilátero inscrito.

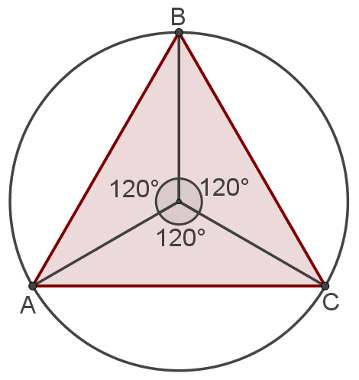
Um triângulo inscrito define três ângulos centrais de 120°

Para perceber isso, veja que o triângulo equilátero divide a circunferência em três partes iguais, como mostra a figura a seguir:

Sendo assim, cada ângulo interno é a terça parte da circunferência completa:

1·360 = 120
3               

Lado do triângulo inscrito é obtido pela expressão:

l = r√3

Nessa expressão, l é a medida do lado do triângulo e r é a medida do raio da circunferência na qual essa figura está inscrita.

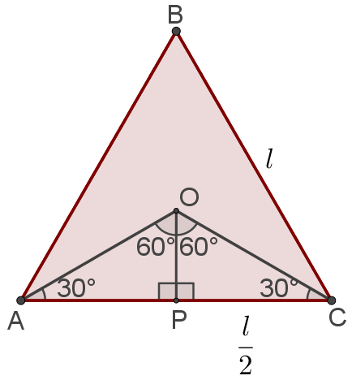
Essa expressão é obtida a partir do próprio triângulo, no qual podem ser demarcados o raio do círculo e o apótema, como feito na imagem a seguir:

O apótema é um segmento de reta que parte do centro de um polígono e vai até o ponto médio de um de seus lados. Como esse triângulo é equilátero, o apótema também é bissetriz e altura do ângulo central AÔC.

Já sabemos, então, que, no triângulo construído, temos um ângulo reto e um ângulo de 60°, como destacado na figura. Além disso, também sabemos que o apótema divide o lado AC ao meio. Assim, o segmento PC da figura mede l/2.

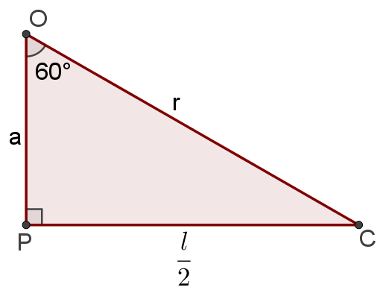
Depois desse procedimento, que também será usado na próxima relação métrica, observe apenas o triângulo POC, em destaque na imagem abaixo:

Se calcularmos o seno de 60° nesse triângulo, temos:

sen60° = l/2
              r

√3 =  l 
 2     2r

√3 =  l 
        r

r√3 = l

l = r√3

Apótema do triângulo equilátero inscrito é dado pela expressão:

a =  r 
     2

Essa expressão é obtida a partir do cálculo do cosseno de 60° no triângulo POC da relação métrica anterior. Calculando cosseno de 60°, temos:

cos60° =  a 
             r

1 =  a 
2     r 

 r = a
2     

Exemplo:

Calcule os comprimentos do apótema e do lado de um triângulo equilátero inscrito em uma circunferência de raio 20 cm.

Solução: Para calcular essas medidas, basta usar as fórmulas dadas para descobrir o apótema e o lado do triângulo equilátero, substituindo nelas a medida do raio da circunferência.

Apótema:

a =  r 
     2

a = 20
     2

a = 10 cm

Lado:

l = r√3

l = 20√3

l = 20·1,73

l = 34,6 cm

Por Luiz Paulo Moreira
Graduado em Matemática