O teorema da bissetriz interna foi desenvolvido especificamente para triângulos e mostra que ao traçarmos a bissetriz interna de um ângulo do triângulo, o ponto de encontro da bissetriz com o lado oposto a ela divide esse lado em segmentos de reta proporcionais aos lados adjacentes desse ângulo. Com a aplicação do teorema da bissetriz interna é possível determinar qual é o valor do lado ou dos segmentos do triângulo utilizando a proporção entre eles.
Veja também: Mediana, bissetriz e altura de um triângulo — qual a diferença?
Tópicos deste artigo
- 1 - Resumo sobre teorema da bissetriz interna:
- 2 - Videoaula sobre o teorema da bissetriz interna
- 3 - Qual é o teorema da bissetriz?
- 4 - Demonstração do teorema da bissetriz interna
- 5 - Exercícios resolvidos sobre teorema da bissetriz interna
Resumo sobre teorema da bissetriz interna:
-
A bissetriz é uma semirreta que divide o ângulo em dois ângulos congruentes.
-
O teorema da bissetriz interna é específico para triângulos.
-
Esse teorema prova que a bissetriz divide o lado oposto em segmentos proporcionais aos lados adjacentes ao ângulo.
Videoaula sobre o teorema da bissetriz interna
Qual é o teorema da bissetriz?
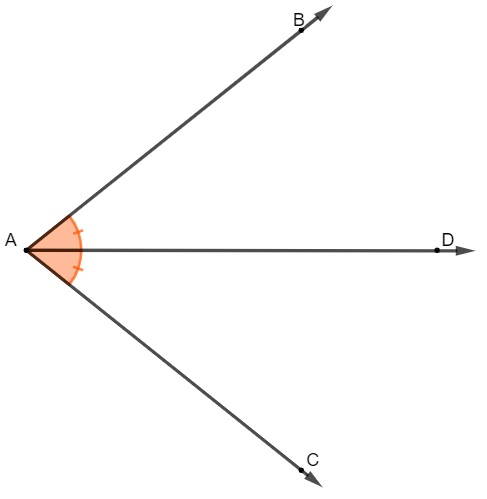
Antes de entendermos o que o teorema da bissetriz interna diz, é importante saber o que é bissetriz de um ângulo. Ela se trata de uma semirreta que divide o ângulo em duas partes congruentes, ou seja, duas partes que possuem a mesma medida.
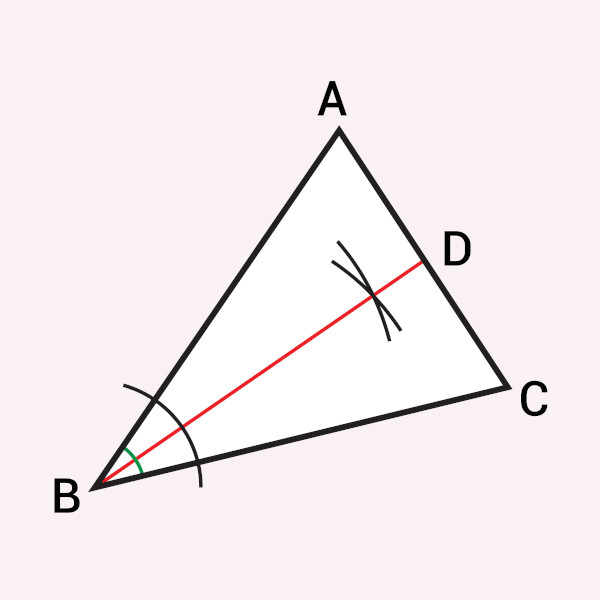
Entendendo o que é a bissetriz, notamos que existe ela existe no ângulo interno de um triângulo. Quando delineamos a bissetriz de um ângulo do triângulo, ela dividirá o lado oposto em dois segmentos. A respeito da bissetriz interna, seu teorema diz que os dois segmentos divididos por ela são proporcionais aos lados adjacentes do ângulo.
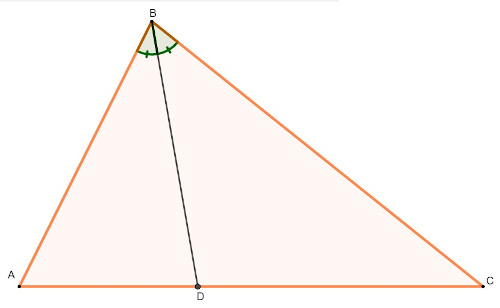
Perceba que a bissetriz divide o lado AC em dois segmentos, o AD e o DC. O teorema da bissetriz mostra que:
\(\frac{\overline{AB}}{\overline{AD}}=\frac{\overline{BC}}{\overline{CD}}\)
Saiba mais: Teorema de Pitágoras — outro teorema desenvolvido para triângulos
Demonstração do teorema da bissetriz interna
No triângulo ABC abaixo, demarcaremos o segmento BD, que é a bissetriz desse triângulo. Além disso, traçaremos o prolongamento do seu lado CB e o segmento AE, paralelo a BD:
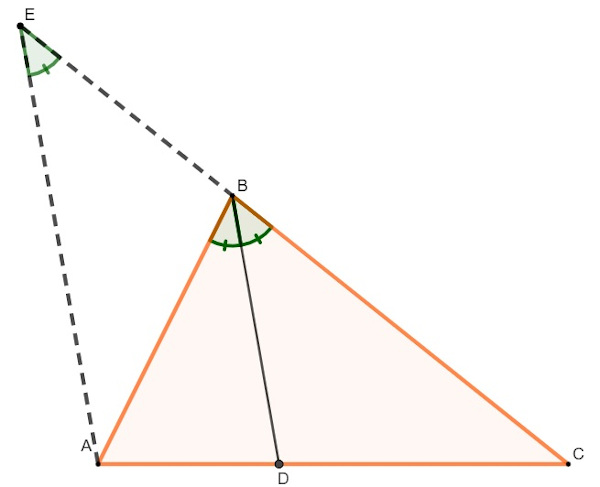
O ângulo AEB é congruente ao ângulo DBC, pois CE é uma reta transversal aos segmentos paralelos AE e BD.
Aplicando o teorema de Tales, concluímos que:
\(\frac{\overline{BE}}{\overline{AD}}=\frac{\overline{BC}}{\overline{DC}}\)
Agora, nos resta demonstrar que BE = AB.
Sendo x a medida do ângulo ABD e DBC, analisando o ângulo ABE, obtemos:
ABE = 180 – 2x
Sendo y a medida do ângulo EAB, temos a seguinte situação:
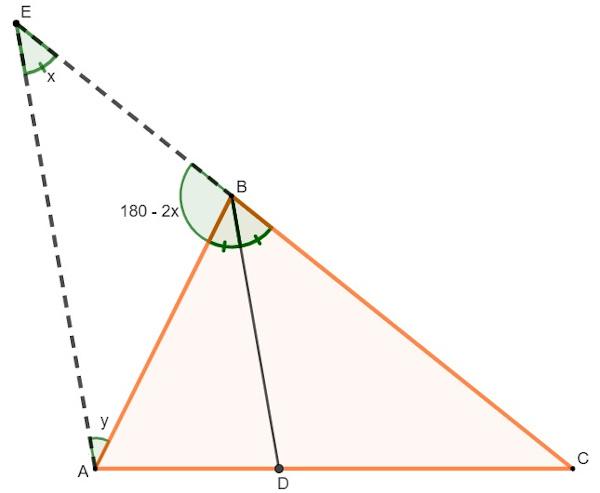
Sabemos que a soma dos ângulos internos do triângulo ABE é 180°, então podemos calcular:
180 – 2x + x + y = 180
– x + y = 180 – 180
– x + y = 0
y = x
Se o ângulo x e o ângulo y possuem a mesma medida, o triângulo ABE é isósceles. Sendo assim, o lado AB = AE.
Como a soma dos ângulos internos de um triângulo é sempre igual a 180°, no triângulo ACE temos:
x + 180 – 2x + y = 180
– x + y = 180 – 180
– x + y = 0
y = x
Como y = x, o triângulo ACE é isósceles. Logo, os segmentos AE e AC são congruentes. Trocando AE por AC na razão, fica provado que:
\(\frac{\overline{AB}}{\overline{AD}}=\frac{\overline{BC}}{\overline{DC}}\)
Exemplo:
Encontre o valor de x no triângulo a seguir:
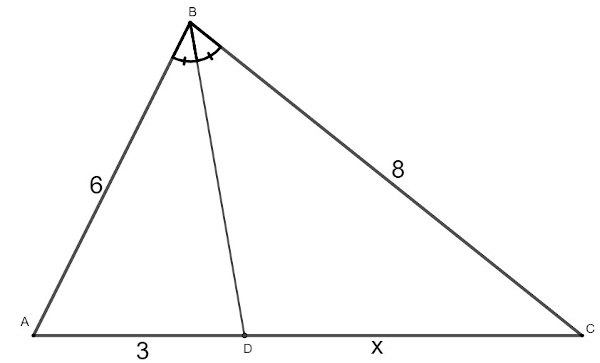
Analisando o triângulo, obtemos a seguinte razão:
\(\frac{6}{3}=\frac{8}{x}\)
Multiplicando de forma cruzada:
6x = 8 ⋅ 3
6x = 24
\(x=\frac{24}{6}\)
x = 4
Leia também: Pontos notáveis de um triângulo — quais são eles?
Exercícios resolvidos sobre teorema da bissetriz interna
Questão 1
Analisando o triângulo a seguir, podemos afirmar que o valor de x é:
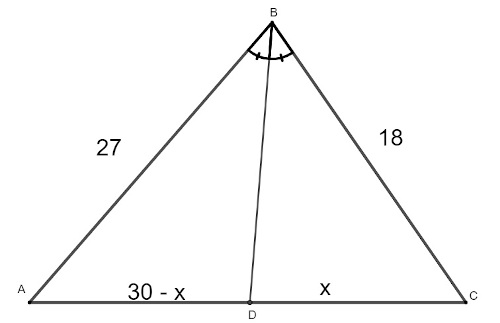
A) 9
B) 10
C) 11
D) 12
E) 13
Resolução:
Alternativa D
Aplicando o teorema da bissetriz interna, obtemos o seguinte cálculo:
\(\frac{27}{30-x}=\frac{18}{x}\)
Multiplicando de forma cruzada:
\(27x=18\ \left(30-x\right)\)
\(27x\ =\ 540\ -\ 18x\ \)
\(27x\ +\ 18x\ =\ 540\ \)
\(45x\ =\ 540\ \)
\(x=\frac{540}{45}\)
\(x\ =\ 12\)
Questão 2
Analise o triângulo a seguir, sabendo que suas medidas foram dadas em centímetro.
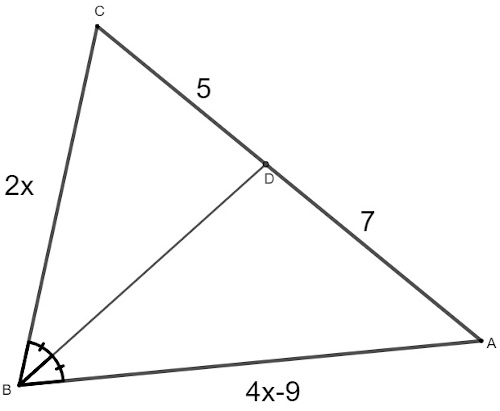
O perímetro do triângulo ABC é igual a:
A) 75 cm
B) 56 cm
C) 48 cm
D) 24 cm
E) 7,5 cm
Resolução:
Alternativa C
Aplicando o teorema da bissetriz, primeiramente encontraremos o valor de x:
\(\frac{2x}{5}=\frac{4x-9}{7}\)
\(5\ \left(4x-9\right)=2x\cdot7\)
\(20x\ -\ 45\ =\ 14x\)
\(20x\ -\ 14x\ =\ 45\ \)
\(6x\ =\ 45\ \)
\(x=\frac{45}{6}\)
\(x\ =\ 7,5\)
Assim, os lados desconhecidos medem:
\(2\cdot7,5\ =\ 15\ \)
\(4\cdot7,5\ -\ 9\ =\ 21\ \)
Lembrando que a medida de comprimento usada foi o cm, o perímetro desse triângulo é igual a:
P = 21 + 15 + 5 + 7 = 48 cm
Por Raul Rodrigues de Oliveira
Professor de Matemática