Ângulos complementares, suplementares e adjacentes

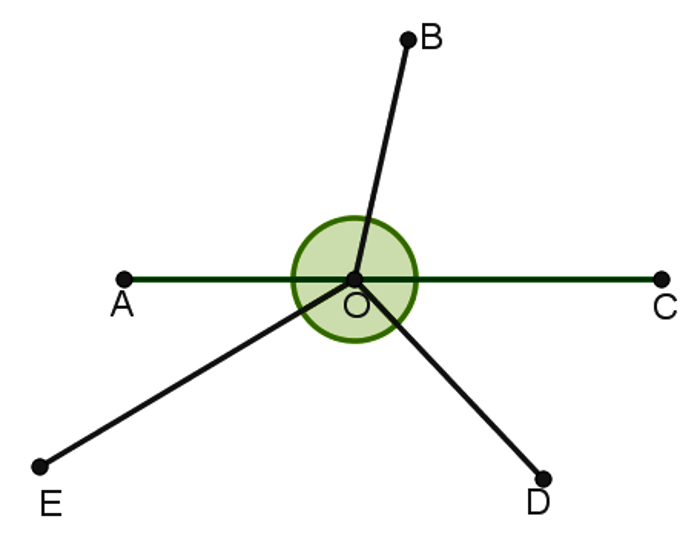
Podemos dizer que um ângulo é a região do plano limitada por duas semirretas de mesma origem. Observe:

Ângulos complementares

Ângulos complementares são dois ângulos em que sua soma resulta em 90º, isto é, um é o complemento do outro.

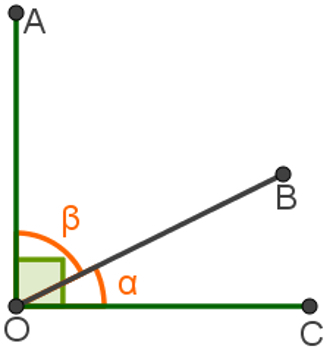
Ângulos cuja soma é igual a 90°

Na ilustração, temos que:

α + β = 90º

α = 90º – β

β = 90º – α

Ângulos suplementares

Ângulos suplementares são dois ângulos que, somados, são iguais a 180º, assim, um é o suplemento do outro.

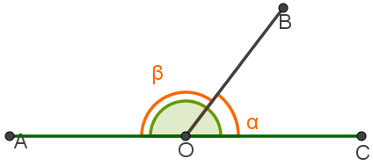
Ângulos cuja soma é igual a 180°

Na ilustração, temos que:

α + β = 180º

α = 180º – β

β = 180º – α

Ângulos adjacentes

Ângulos adjacentes são aqueles que possuem um lado em comum, mas as regiões determinadas não possuem pontos em comum. Observe a ilustração:

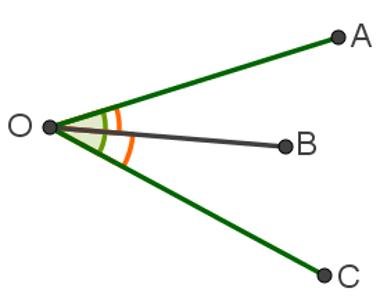
Ângulos que possuem lado em comum

Os ângulos AÔB e BÔC são adjacentes, pois possuem o lado OB em comum, mas suas regiões determinadas não possuem pontos em comum.

Os ângulos AÔC e AÔB não são adjacentes, embora possuam um lado em comum, pois suas regiões determinadas possuem pontos em comum. A região AÔB pertence à região AÔC.

Ângulos adjacentes e suplementares

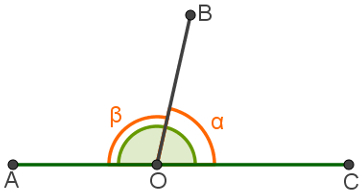
De acordo com a ilustração acima, os ângulos AÔB e BÔC são adjacentes, pois possuem o lado OB em comum e suas áreas determinadas não possuem duplicidade de pontos. São também suplementares, pois a soma dos ângulos α e β totaliza 180º.

Por Marcos Noé
Graduado em Matemática