Plano é uma das noções primitivas da Geometria. Essas noções referem-se a objetos que não possuem definição, mas que são fundamentais para todas as definições, propriedades e características das figuras e sólidos geométricos. As outras noções primitivas são ponto, reta e espaço.
O que é um plano?
O plano é uma superfície ilimitada sobre a qual é possível construir retas concorrentes. Dessa maneira, não há curvatura em um plano, portanto, sobre ele não é possível obter profundidade, embora existam técnicas para representar figuras tridimensionais em planos.
Geralmente, os planos são compreendidos como uma sequência infinita e ilimitada de retas alinhadas “linearmente”, como mostra a imagem a seguir.

Axiomas sobre planos
Axiomas (ou postulados) são afirmações que não podem ser demonstradas, mas quesão indispensáveis para validar as propriedades da Matemática. Com relação aos planos, os axiomas garantem sua existência e o modo de se obter um plano.
O axioma que garante a existência dos planos é o seguinte:
Existe plano e tanto nele quanto fora dele existem pontos.
Assim, além da existência dos planos, esse axioma garante a existência de um espaço fora deles. O axioma que fala sobre o modo de se obter um plano, conhecido como axioma de determinação, é o seguinte:
Três pontos não colineares determinam um único plano que os contém.
“Não colineares” é o mesmo que dizer que esses três pontos não podem pertencer a uma mesma reta.
Determinando planos
Os planos podem ser obtidos de quatro maneiras diferentes. Observe que todas elas baseiam-se no axioma de determinação.
→ Utilize o próprio axioma de determinação
Lembre-se de que três pontos não colineares determinam um plano único. Assim sendo, onde houver essas condições, haverá um plano.
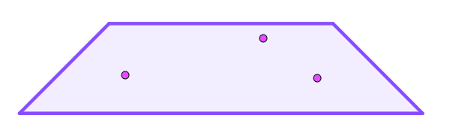
Três pontos distintos e não colineares que determinam um plano
→ Utilize uma reta e um ponto fora dela
Para perceber que uma reta e um ponto fora dela determinam um plano, basta notar que a reta possui infinitos pontos, portanto, possui dois pontos distintos que podem ser escolhidos com facilidade. Tomando dois pontos quaisquer de uma reta e um ponto fora dela, teremos três pontos não colineares. Assim sendo, basta aplicar o axioma da determinação (três pontos não colineares determinam um único plano).
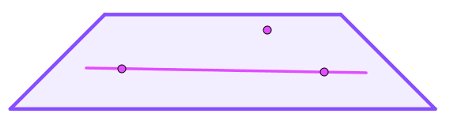
Plano formado por uma reta e um ponto fora dela
→ Utilize duas retas concorrentes
Para perceber que duas retas concorrentes determinam um plano, basta escolher um ponto A qualquer sobre a primeira e um ponto B qualquer sobre a segunda e o ponto O de interseção entre elas. Observe que o ponto O e o ponto B pertencem a uma mesma reta, mas o ponto A não. Assim, temos três pontos não colineares, condição suficiente para aplicar o axioma da determinação.
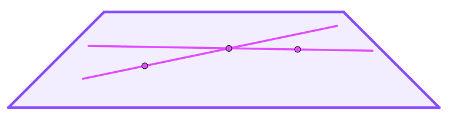
Plano formado por duas retas concorrentes
→ Utilize duas retas paralelas
Duas retas paralelas determinam um plano da seguinte maneira: tomando dois pontos distintos sobre a primeira reta e um ponto qualquer sobre a segunda, temos três pontos não colineares.

Plano formado por duas retas paralelas
Por Luiz Paulo Moreira
Graduada em Matemática

