Para que polígonos sejam considerados inscritos ou circunscritos, deve existir uma circunferência que sirva como base para isso. O fato de eles serem circunscritos ou inscritos diz respeito a um caso especial de posições relativas entre o polígono e a circunferência.
Antes de aprender a construir polígonos e circunferências que sejam inscritos, é importante relembrar a definição dessas figuras.
Definição de polígono inscrito e polígono regular inscrito
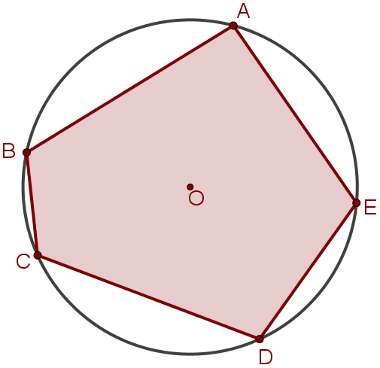
Um polígono é dito inscrito em uma circunferência quando todos os seus vértices são pontos pertencentes a ela.
A construção de polígonos inscritos pode ser feita a partir de pontos da circunferência. Assim, para construir um pentágono inscrito em uma circunferência, como o da imagem acima, escolha cinco pontos pertencentes a ela e trace as cordas que ligam os pontos consecutivos.
A definição do polígono regular inscrito na circunferência é igual à de um polígono qualquer inscrito nela. A diferença é que, nesse caso, o polígono deverá ser regular. Isso significa que todos os seus ângulos terão a mesma medida e que todos os seus lados serão congruentes.
Técnicas para a construção de um polígono regular
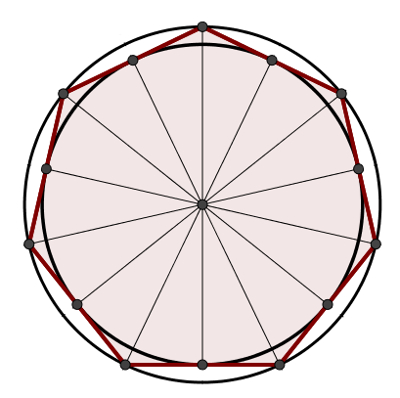
1 – Divida a circunferência em x arcos com o mesmo comprimento de modo que x seja o número de lados do polígono inscrito nela. As cordas que ligam as divisões consecutivas de arcos formarão o polígono regular inscrito.
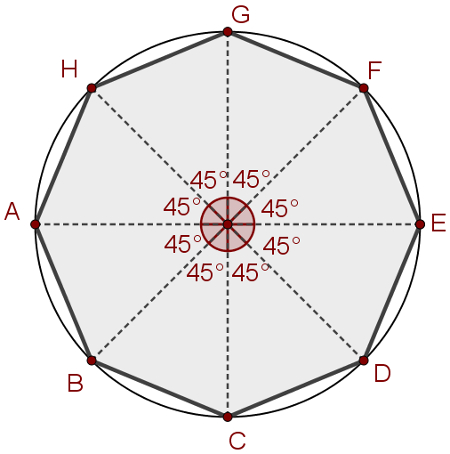
Essa divisão pode ser feita utilizando a regra de três para determinar o ângulo central relativo a cada arco. Dessa forma, para construir o octógono regular inscrito, por exemplo, dividiremos o círculo em oito arcos iguais. O ângulo central relativo a eles deverá ser 360° dividido por 8, que tem 45° como resultado. Depois disso, basta traçar as cordas que ligam as extremidades consecutivas de cada arco, como na imagem a seguir:
2 – A partir do polígono regular, construa a circunferência que possui todos os seus vértices. Essa construção sempre será possível para todo polígono regular.
Circunferência inscrita
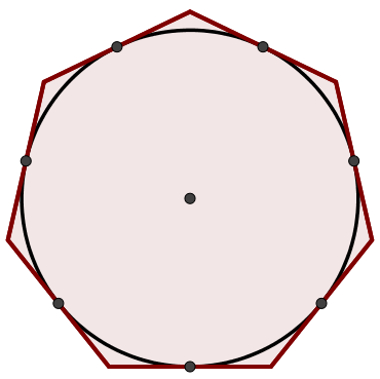
Também existe a possibilidade de a circunferência estar inscrita no polígono. Para que isso aconteça, basta que todos os lados desse polígono sejam tangentes à circunferência, como mostra a figura a seguir:
Construção da circunferência inscrita no polígono regular
Em um polígono regular qualquer, encontre seu centro, que também será o centro da circunferência. Para isso, trace duas mediatrizes de lados distintos do polígono. Como ele é regular, o ponto de encontro dessas retas será o centro do polígono e, consequentemente, o centro da circunferência.
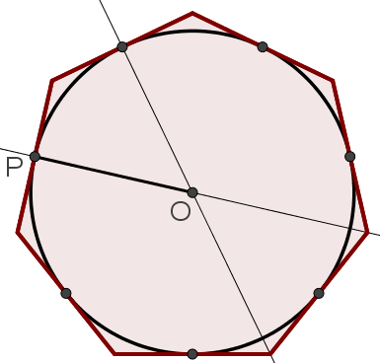
Na figura a seguir, observe os pontos O e P que são, respectivamente, o cento da circunferência e a intersecção entre uma mediatriz e um lado. Se o segmento OP for usado como raio para construção de uma circunferência de centro O, essa circunferência ficará automaticamente inscrita no polígono, como mostra a imagem a seguir:
A definição de circunferência inscrita é equivalente à definição de polígono circunscrito. Em outras palavras, também poderíamos dizer que o heptágono da imagem anterior circunscreve a circunferência.
Por Luiz Paulo Moreira
Graduado em Matemática