O cálculo de área é uma atividade cotidiana na vida de todos nós. Sempre nos vemos envolvidos em alguma situação em que há a necessidade de se calcular a área de uma forma geométrica plana. Seja na aquisição de um terreno, na reforma de um imóvel ou na busca de reduzir custos com embalagens, o uso do conhecimento de cálculo de áreas se faz presente. É uma atividade muito simples, mas às vezes deixamos algumas questões passarem despercebidas.
Um professor de matemática, durante a aula de geometria plana, fez a seguinte indagação aos seus alunos: Temos um retângulo com área de x metros quadrados. Se duplicarmos as medidas dos lados desse retângulo, o que ocorrerá com o valor da área? Um dos alunos imediatamente respondeu: a área dobrará de tamanho, ou seja, será de 2x metros quadrados! O professor imediatamente retrucou: De forma alguma, será mais que o dobro.
Vejamos a explicação de tal fato.
Primeiro, faremos um exemplo conhecendo as medidas do retângulo, depois faremos a generalização.
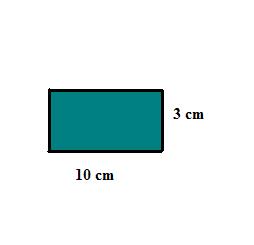
Exemplo 1. Considere o retângulo abaixo:
Sua área será de:
A1 = 10 x 3 = 30 cm2
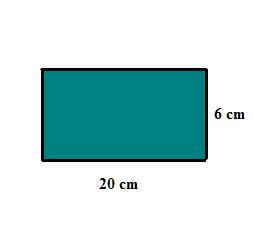
Agora, vamos duplicar as medidas dos lados.
A área desse novo retângulo será de:
A2 = 20 x 6 = 120 cm2
Observe que ao dobrar as medidas dos lados do retângulo sua área mais que dobrou, na verdade quadruplicou. Mas será que isso ocorre para qualquer retângulo?
Vejamos, agora, um caso genérico, a fim de verificar essa propriedade para todo retângulo.
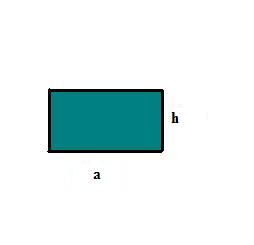
Vamos considerar um retângulo de base b e altura h, como mostra a figura.
Sua área é dada por: A1 = a x h
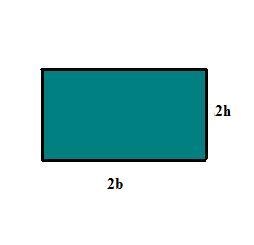
Agora, vamos dobrar as suas medidas, ou seja, a base será 2b e a altura, 2h.
A área desse retângulo será dada por: A2 = 2b x 2h = 4(b x h) = 4A1.
Observe que para qualquer retângulo, se dobrarmos as medidas de seus lados, a área quadruplicará.
Vamos fazer a análise dessa situação para outras figuras planas.
Circunferência:
Numa circunferência de raio r, a área será de: πr2.
Se dobrarmos a medida do raio, ou seja, o raio sendo 2r, a área será de: π(2r)2 = π4r2 = 4πr2.
Podemos observar que ao dobrar o valor do raio, a área da circunferência também quadruplica.
Triângulo Equilátero
Num triângulo equilátero de lado L, sua área será de:
![]()
Ao dobrarmos a medida do lado, ou seja, o triângulo possuir lado medindo 2L, a área passará a ser de:
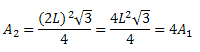
Concluímos que ao dobrar as medidas dos lados de um triângulo equilátero, sua área quadruplica.
De maneira geral, a conclusão é que, ao dobrar a medida das dimensões de uma figura plana, suas áreas tem o valor mais que duplicado.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola