O que são pontos de máximo e de mínimo?

Os pontos de máximo e de mínimo são definidos e discutidos apenas para funções do segundo grau, uma vez que eles podem existir em qualquer curva.

Antes, vamos relembrar: uma função do segundo grau é aquela que pode ser escrita na forma f(x) = ax² + bx + c. O gráfico desse tipo de função é a parábola, que pode ter sua concavidade voltada para baixo ou para cima. Além disso, nessa figura, existe um ponto chamado vértice, representado pela letra V, que é pode ser o ponto de máximo ou o ponto de mínimo da função.

Ponto de máximo

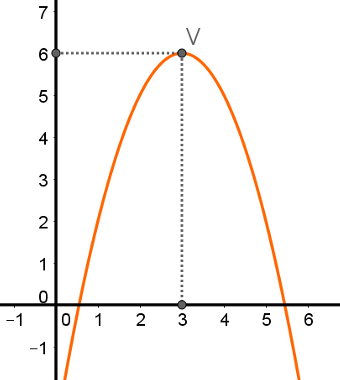
Toda função do segundo grau com a < 0 possui ponto de máximo. Em outras palavras, o ponto de máximo somente é possível em funções com a concavidade voltada para baixo. Como mostra a imagem a seguir, o ponto de máximo V é o ponto mais alto das funções do segundo grau com a < 0.

Observe que o gráfico dessa função é crescente até chegar ao ponto de máximo, depois disso, o gráfico torna-se decrescente. O ponto mais alto dessa função do exemplo é seu ponto de máximo. Note também que não existe nenhum ponto com coordenada y superior a V = (3, 6) e que o valor de x atribuído ao ponto de máximo fica no ponto médio do segmento, cujas extremidades são as raízes da função (quando elas forem números reais).

Além disso, lembre-se de que o ponto de máximo sempre coincide com o vértice da função com concavidade voltada para baixo.

Ponto de mínimo

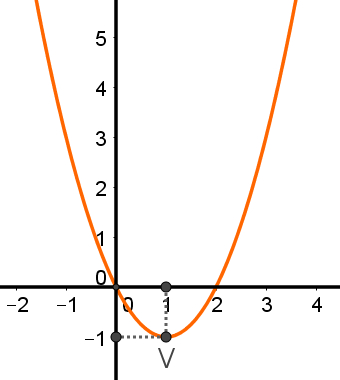
Toda função do segundo grau com o coeficiente a > 0 possui ponto de mínimo. Em outras palavras, o ponto de mínimo somente é possível em funções com concavidade voltada para cima. Observe na figura a seguir que V é o ponto mais baixo da parábola:

O gráfico dessa função é decrescente até chegar ao ponto de mínimo, depois disso, segue crescente. Além disso, o ponto de mínimo V é o ponto mais baixo dessa função, ou seja, não existe outro ponto com coordenada y inferior a – 1. Note também que o valor de x relacionado a y no ponto mínimo também fica no ponto médio do segmento, cujas extremidades são as raízes da função (quando elas forem números reais).

Lembre-se também de que o ponto de mínimo sempre coincide com o vértice da função com concavidade voltada para cima.

Ponto de máximo ou de mínimo na lei de formação da função

Sabendo que a lei de formação da função do segundo grau tem a forma f(x) = ax² + bx + c, é possível utilizar relações entre os coeficientes a, b e c para encontrar as coordenadas do vértice da função. As coordenadas do vértice serão justamente as coordenadas do seu ponto de máximo ou de mínimo.

Sabendo que a coordenada x do vértice de uma função é representada por xv, teremos:

x_v = – b
       2a

Sabendo que a coordenada y do vértice de uma função é representada por yv, teremos:

y_v = – Δ
       4a

Portanto, as coordenadas do vértice V serão: V = (x_v, y_v).

Se o vértice será ponto de máximo ou de mínimo, basta analisar a concavidade da parábola:

Se a < 0, a parábola possui ponto de máximo.

Se a > 0, a parábola possui ponto de mínimo.

Observe que, quando a função possui duas raízes reais, x_v ficará no ponto médio do segmento, cujas extremidades são as raízes da função. Assim, outra técnica para encontrar x_v e y_v é descobrir as raízes da função, encontrar o ponto médio do segmento de reta que as liga e aplicar esse valor na função para descobrir y_v relacionado.

Exemplo:

Determine o vértice da função f(x) = x² + 2x – 3 e diga se ele é ponto de máximo ou de mínimo.

1ª Solução: Calcule as coordenadas do vértice pelas fórmulas dadas, sabendo que a = 1, b = 2 e c = – 3.

x_v = – b
       2a

x_v = – 2
        2·1

x_v = – 1

y_v = – Δ
       4a

y_v = – (2² – 4·1·[– 3])
     4·1

y_v = – (4 + 12)
      4

y_v = – 16
        4

y_v = – 4

Então, V = (– 1, – 4) e a função possuem ponto de mínimo, pois a = 1 > 0.

2ª Solução: Encontre as raízes da função do segundo grau, determine o ponto médio do segmento que as liga, o qual será x_v, e aplique esse valor na função para descobrir y_v.

As raízes da função, dadas pelo método de completar quadrados, são:

f(x) = x² + 2x – 3

0 = x² + 2x – 3

4 = x² + 2x – 3 + 4

x² + 2x + 1 = 4

(x + 1)² = 4

Fazendo a raiz quadrada em ambos os membros, teremos:

√[(x + 1)²] = √4
x + 1 = ± 2
x = ± 2 – 1

x’ = 2 – 1 = 1

x” = – 2 – 1 = – 3

Um segmento que vai de – 3 até 1 tem como ponto médio x_v = – 1. Para mais detalhes, confira a imagem após a solução. Aplicando x_v na função, teremos:

f(x) = x² + 2x – 3

y_v = (– 1)² + 2(– 1) – 3

y_v = 1 – 2 – 3

y_v = 1 – 5

y_v = – 4

Esses resultados são os mesmos valores encontrados na primeira solução: V = (– 1, – 4). Além disso, a função possui ponto de mínimo, pois a = 1 > 0.

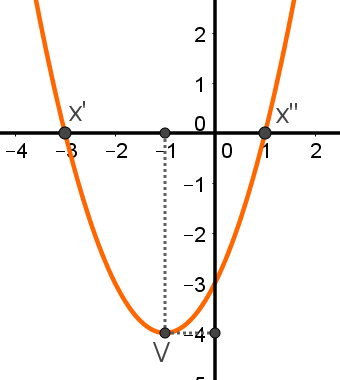
A imagem abaixo mostra o gráfico dessa função com suas raízes e com o seu ponto de mínimo V.

Vale comentar que a fórmula de Bháskara também pode ser usada para encontrar as raízes da função nesse conteúdo.

Por Luiz Paulo Moreira
Graduado em Matemática