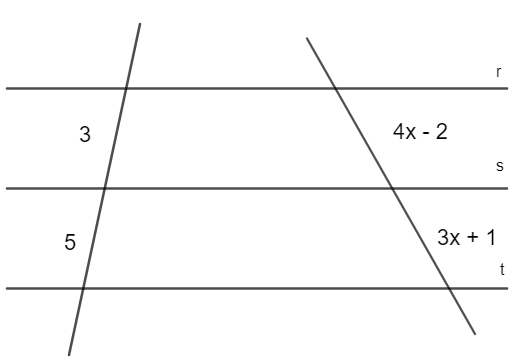
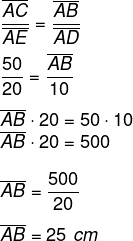O teorema de Tales foi desenvolvido pelo matemático Tales de Mileto, que demonstrou a existência de uma proporcionalidade nos segmentos de reta formados por retas paralelas cortadas por retas transversais.
A partir desse teorema, é possível perceber relações de proporcionalidade em várias situações, o que tem vasta aplicação, como na astronomia e em triângulos. Tales de Mileto foi um filósofo pré-socrático que deu grandes contribuições não só para a filosofia, mas também para a matemática, na busca de compreender melhor o Universo.
Tópicos deste artigo
- 1 - Enunciado do teorema de Tales
- 2 - Como aplicar o teorema de Tales
- 3 - Teorema de Tales em triângulos
- 4 - Exercícios resolvidos
Enunciado do teorema de Tales
O teorema de Tales afirma que:
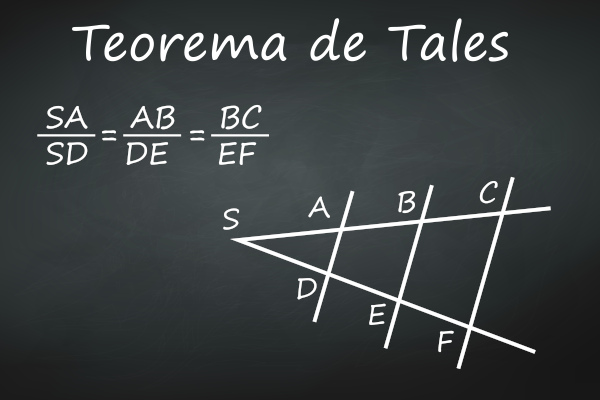
Um feixe de retas paralelas determina sobre duas retas transversais segmentos proporcionais.
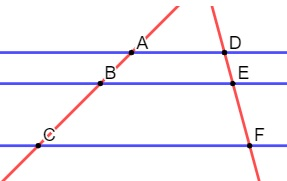
Na imagem, há vários segmentos de reta: AB, BC, DE, EF, AC, DF. É possível compará-los de duas formas. Uma delas é comparar os segmentos de uma mesma reta transversal:
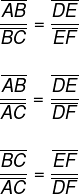
Outra maneira de realizar essa comparação, mas que ainda assim gera o mesmo resultado, é montar a razão entre o segmento de uma reta transversal sob o segmento equivalente.
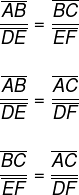
Independentemente da forma escolhida para montar as proporções, é possível encontrar o valor desses segmentos a partir da propriedade fundamental da proporção.
Veja também: Medidas de comprimento – unidades de medida e conversão
Como aplicar o teorema de Tales
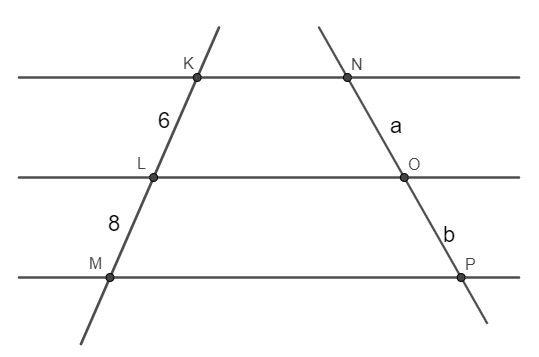
Na prática, utiliza-se o teorema de Tales com o objetivo de encontrar valores desconhecidos de situações que envolvem retas paralelas e retas transversais.
Exemplo:
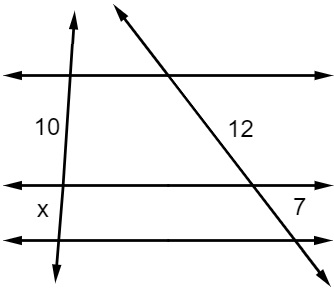
Montando a proporção, temos que 10 está para x, assim como 12 está para 7, ou seja:
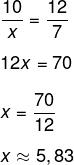
Teorema de Tales em triângulos
Uma das aplicações mais importantes do teorema de Tales é no estudo de triângulos. Ao traçar uma reta paralela à base, é possível construir um triângulo menor semelhante ao triângulo maior. Além disso, os segmentos formados pela lateral do triângulo também são proporcionais, o que possibilita a aplicação do Teorema de Tales para encontrar valores desconhecidos nesse triângulo.
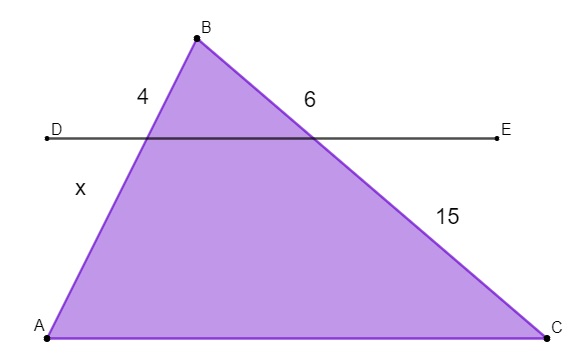
Exemplo:
Calcule o valor de BD sabendo que o segmento de reta DE é paralelo à base do triângulo AC.
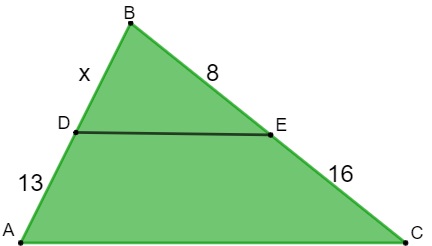
Montando a proporção, sabemos que x está para 13, assim como 8 está para 16.
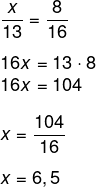
Leia também: Classificação de triângulos – critérios e nomenclatura
Exercícios resolvidos
Questão 1 - (Fuvest) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de x, y e z em metros sabendo que a frente total para essa rua tem 180 m?
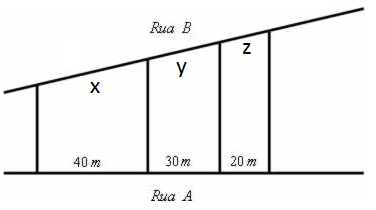
A) 90, 60 e 30
B) 40, 60 e 90
C) 80, 60 e 40
D) 20, 30 e 40
Resolução
Alternativa C.
Sabemos que a soma de x + y + z = 180 m.
Somando os lados da rua A, temos que: 40 + 30 + 20 = 90 m.
Montando as proporções para encontrar o valor de x, temos:
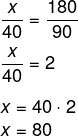
Assim sendo, x = 80 metros. Agora encontraremos o valor de y:
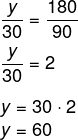
Como y = 60 metros, podemos então encontrar o valor de z:
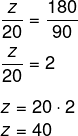
Questão 2 - (IFG) Seja o triângulo ABC da figura a seguir com as seguintes medidas: AC = 50 cm, AE = 20 cm, e AD= 10 cm.
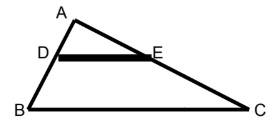
Sabendo que DE é paralelo à BC, a medida do lado AB é de?
A) 15 cm
B) 20 cm
C) 25 cm
D) 30 cm
E) 35 cm
Resolução
Alternativa C.
Como DE é paralelo a BC, podemos aplicar o teorema de Tales.
Dados: AC = 50 cm, AE = 20 cm e AD = 10 cm.
Sabemos que AC está AE, assim como AD está para AB.