O paralelepípedo é um sólido geométrico estudado na Geometria Espacial, bastante presente no nosso cotidiano. Caixas, alguns prédios e vários outros objetos possuem formato de paralelepípedo.
Para que um sólido geométrico seja considerado paralelepípedo, ele precisa possuir faces formadas por paralelogramos — faces possuindo formato de retângulos, quadrados ou losangos, por exemplo. Vale dizer também que um paralelepípedo pode ser reto ou oblíquo.
Para calcular o volume de um paralelepípedo, calculamos o produto entre a área da base e a altura, mas existem também fórmulas para o cálculo da área total e da diagonal.
Leia também: Área dos sólidos geométricos — fórmulas e exemplos de cálculo das principais figuras
Tópicos deste artigo
- 1 - Resumo sobre paralelepípedo
- 2 - Videoaula sobre o paralelepípedo
- 3 - Elementos e características do paralelepípedo
- 4 - Classificação do paralelepípedo
- 5 - Fórmulas do paralelepípedo
- 6 - Exercícios resolvidos sobre paralelepípedo
Resumo sobre paralelepípedo
-
O paralelepípedo é um sólido geométrico que possui faces formadas por paralelogramos.
-
É composto por 8 vértices, 12 arestas e 6 faces.
-
É classificado como reto quando suas arestas são perpendiculares e como oblíquo quando suas arestas não são perpendiculares.
-
Para calcular o volume de um paralelepípedo reto ou oblíquo, utilizamos a fórmula:
\(V=A_b\cdot h\)
-
Considerando um paralelepípedo reto, com lados da base medindo a e b e altura c, seu volume pode ser calculado por:
\(V=a\cdot b\ \cdot c\)
-
O paralelepípedo oblíquo não possui fórmulas específicas para o cálculo da área total e da diagonal, já o paralelepípedo reto, sim.
-
A área total do paralelepípedo reto é calculada pela fórmula:
\(A=2ab+2ac+2bc\)
-
A diagonal de um paralelepípedo reto é calculada por:
\(d=\sqrt{a^2+b^2+c^2}\)
Videoaula sobre o paralelepípedo
Elementos e características do paralelepípedo
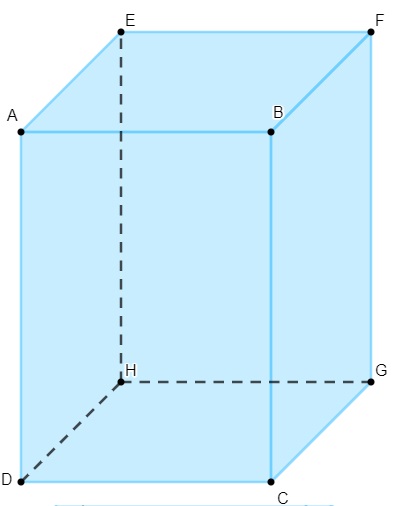
Os principais elementos de um sólido geométrico são as suas faces, suas arestas e seus vértices. O paralelepípedo é composto por 6 faces, 8 vértices e 12 arestas.
-
Os 8 vértices são os pontos A, B, C, D, E, F, G, H.
-
As 12 arestas são os segmentos \(\overline{AB},\overline{BC},\overline{CD},\overline{AD},\overline{AE},\overline{EF},\overline{BF},\overline{FG},\overline{GH},\overline{EH},\overline{CG},\overline{DH}\).
-
As 6 faces são os paralelogramos ABCD, ABEF, CDHG, ADHE, BCGF, EFGH.
Classificação do paralelepípedo
Os paralelepípedos podem ser classificados de duas maneiras distintas. Há os paralelepípedos retos e os paralelepípedos oblíquos. O paralelepípedo é reto quando a sua aresta lateral forma um ângulo de 90° com a aresta da base e é oblíquo quando existe uma inclinação diferente de 90° entre a aresta da base e a aresta lateral.
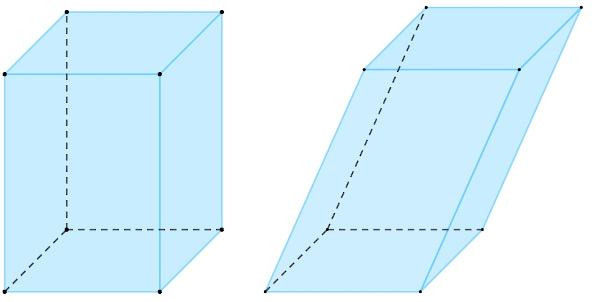
O paralelepípedo reto possui fórmulas específicas para o cálculo de volume, área total e diagonal. Vejamos a seguir cada uma delas.
Fórmulas do paralelepípedo
As fórmulas do paralelepípedo servem para calcular o volume, a área total e a diagonal de um paralelepípedo reto. O paralelepípedo oblíquo possui fórmula para o cálculo do volume, porém ele não possui fórmula específica para o cálculo da área e da diagonal, por causa dos formatos que ele pode assumir.
-
Fórmula para cálculo do volume do paralelepípedo
Para calcular o volume de um paralelepípedo qualquer (reto ou oblíquo), utilizamos a fórmula:
|
\(V=A_b\cdot h\) |
-
\(A_b\): área da base
-
h: altura do paralelepípedo
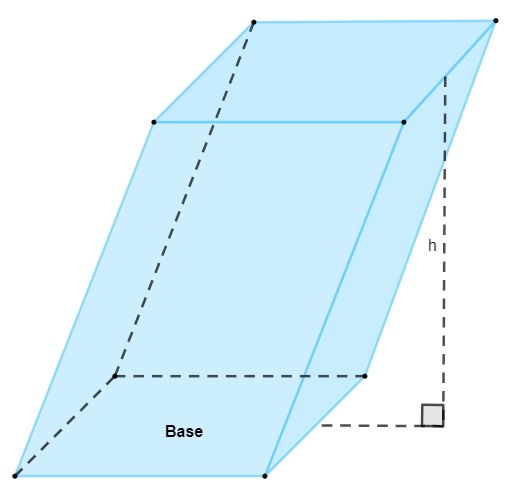
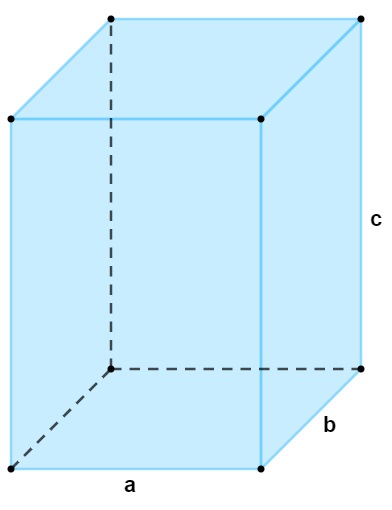
Especificamente no paralelepípedo reto, a base é composta por um retângulo. Assim, a área da base é igual ao produto entre as duas dimensões da base. Para calcular o volume, basta multiplicar o valor pela altura. Logo, o volume de um paralelepípedo reto é o produto entre o comprimento, a largura e a altura.
|
\(V\ =\ a\ \cdot b\ \cdot c\) |
-
Fórmula para cálculo de área do paralelepípedo
A área de um sólido geométrico é a soma das áreas das suas faces. Como as faces do paralelepípedo retângulo são todas retângulos, a área de cada face é igual ao produto entre o comprimento e a largura da face. Entretanto, faces paralelas possuem a mesma medida, então para calcular a área de um paralelepípedo reto utilizamos a fórmula:
|
\(A=2(ab+ac+bc)\) |
-
Fórmula para cálculo da diagonal do paralelepípedo
Conhecemos como diagonal de um paralelepípedo o segmento de reta que liga um vértice ao vértice oposto a ele, como na imagem a seguir:
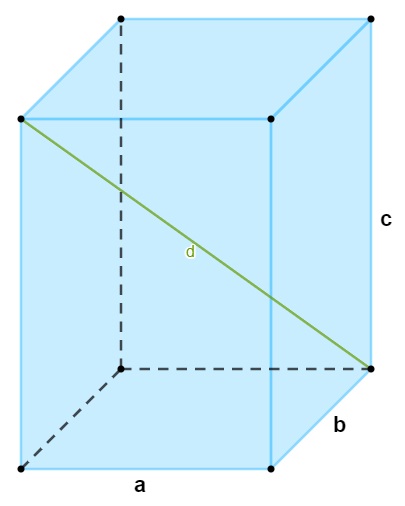
Para calcular o comprimento da diagonal de um paralelepípedo reto, utilizamos a fórmula:
|
\(d=\sqrt{a^2+b^2+c^2}\) |
Leia também: Fórmulas para cálculo do volume dos principais sólidos geométricos
Exercícios resolvidos sobre paralelepípedo
Questão 1
Uma caixa possui formato de um paralelepípedo reto com dimensões de 50 cm de largura, 85 cm de comprimento e 62 cm de altura. A medida da área total dessa caixa é de:
A) 25.240 cm²
B) 26.120 cm²
C) 27.000 cm²
D) 28.150 cm²
E) 28.320 cm²
Resolução:
Alternativa A
Calculando a área total, temos que:
\(A=2\left(50\cdot85+50\cdot62+62\cdot85\right)\)
\(A=2\cdot12.620\)
\(A=25.240\ cm^2\ \ \)
Questão 2
(IFG 2017) A água da piscina de saltos ornamentais do Centro Aquático Maria Lenk, no Parque Olímpico da Barra (Rio 2016), ficou verde. O Comitê Olímpico justificou a coloração devido a 80 litros de peróxido de hidrogênio (água oxigenada) jogados na água, que criou uma reação para o cloro que neutralizou sua habilidade de matar organismos. Para a competição, a água de toda a piscina foi trocada. Suponha que essa piscina tenha o mesmo volume de um paralelepípedo reto com 23 metros de comprimento, 18 metros de largura e 9 metros de profundidade. Qual o volume de água que foi trocado desta piscina, em litros? (Adote 1 m³ = 1000 litros).
A) 3,726 milhões.
B) 4,140 milhões.
C) 2,070 milhões.
D) 1,620 milhões.
E) 2,125 milhões.
Resolução:
Alternativa A
Para calcular o volume, multiplicaremos as três dimensões:
\(V=18\cdot9\cdot23\)
\(V=3726\ m³\)
Como o volume é dado em litros, multiplicaremos por 1000:
\(V\ =\ 3726\ \cdot1000\ =\ 3\ 726\ 000\ litros\)


