Aplicações do Teorema de Pitágoras

O teorema de Pitágoras é uma das relações métricas do triângulo retângulo, isto é, é uma igualdade capaz de relacionar as medidas dos três lados de um triângulo nessas condições. É possível descobrir, por meio desse teorema, a medida de um dos lados de um triângulo retângulo conhecendo as outras duas medidas. Por causa disso, existem diversas aplicações para o teorema na nossa realidade.

Teorema de Pitágoras e o triângulo retângulo

Um triângulo é chamado retângulo quando possui um ângulo reto. É impossível que um triângulo possua dois ângulos retos, pois a soma de seus ângulos internos é obrigatoriamente igual a 180°. O lado desse triângulo que se opõe ao ângulo reto é chamado hipotenusa. Os outros dois lados são chamados catetos.

Diante disso, o teorema de Pitágoras faz a seguinte afirmação, válida para todo triângulo retângulo:

“O quadrado da hipotenusa é igual à soma dos quadrados dos catetos”

Matematicamente, se a hipotenusa do triângulo retângulo é “x” e os catetos são “y” e “z”, o teorema de Pitágoras garante que:

x² = y² + z²

Aplicações do teorema de Pitágoras

1º Exemplo

Um terreno tem formato retangular, de modo que um de seus lados mede 30 metros e o outro mede 40 metros. Será preciso construir uma cerca que passe pela diagonal desse terreno. Assim, considerando-se que cada metro de cerca custará R$ 12,00, quanto será gasto, em reais, para sua construção?

Solução:

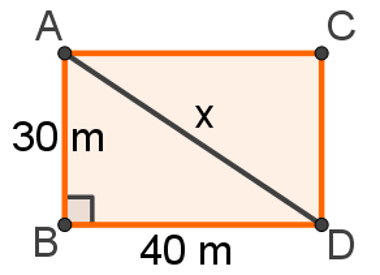
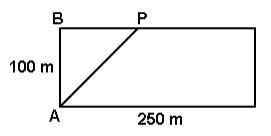
Se a cerca passa pela diagonal do retângulo, então, basta calcular o seu comprimento e multiplicá-lo pelo valor de cada metro. Para encontrar a medida da diagonal de um retângulo, devemos observar que esse segmento divide-o em dois triângulos retângulos, como mostra a figura a seguir:

Tomando somente o triângulo ABD, AD é hipotenusa e BD e AB são catetos. Portanto, teremos:

x² = 30² + 40²

x² = 900 + 1600

x² = 2500

x = √2500

x = 50

Dessa forma, sabemos que o terreno terá 50 m de cerca. Como cada metro custará 12 reais, portanto:

50·12 = 600

Serão gastos R$ 600,00 nessa cerca.

2º Exemplo

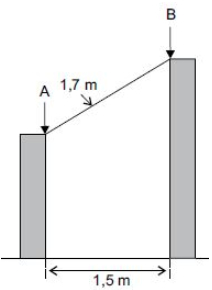
(PM-SP/2014 – Vunesp). Duas estacas de madeira, perpendiculares ao solo e de alturas diferentes, estão distantes uma da outra 1,5 m. Será colocada entre elas uma outra estaca de 1,7 m de comprimento que ficará apoiada nos pontos A e B, conforme mostra a figura.

A diferença entre a altura da maior estaca e a altura da menor estaca, nessa ordem, em cm, é:

a) 95

b) 75

c) 85

d) 80

e) 90

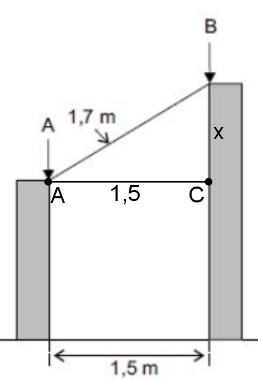
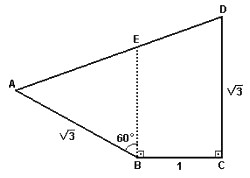
Solução: A distância entre as duas estacas é igual a 1,5 m, se medida no ponto A, formando o triângulo retângulo ABC, conforme indicado na figura a seguir:

Usando o teorema de Pitágoras, teremos:

AB² = AC² + BC²

1,7² = 1,5² + BC²

1,7² = 1,5² + BC²

2,89 = 2,25 + BC²

BC² = 2,89 – 2,25

BC² = 0,64

BC = √0,64

BC = 0,8

A diferença entre as duas estacas é igual a 0,8 m = 80 cm. Alternativa D.

Por Luiz Paulo
Graduado em Matemática