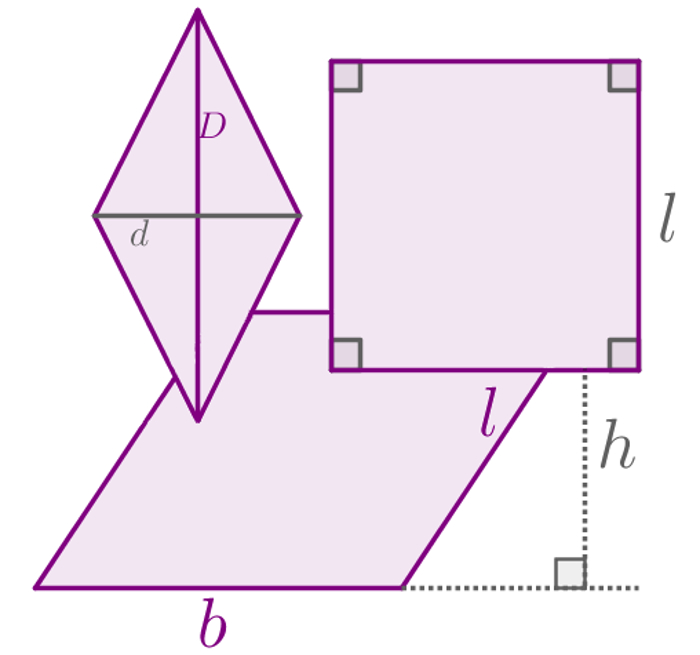
Os paralelogramos são polígonos que possuem quatro lados, dois a dois paralelos. Pertencem ao conjunto dos paralelogramos as seguintes figuras: quadrados, retângulos, losangos e outros paralelogramos que não possuem características específicas para serem classificados. A fórmula usada para calcular a área de cada uma dessas figuras varia de acordo com suas características específicas. A seguir, confira a fórmula para o cálculo de cada uma dessas áreas.
Área do paralelogramo
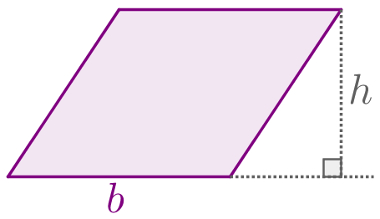
Uma figura que possui lados opostos paralelos é chamada de paralelogramo. Uma das consequências dessa definição mais exploradas em vestibulares e Enem é o fato de os lados opostos serem congruentes. Essas propriedades específicas podem ser estudadas mais amplamente aqui. Para calcular a área do paralelogramo (AP), podemos usar a seguinte fórmula:
AP = b·h
-
b = base do paralelogramo, que costuma ser a medida do lado voltado para baixo;
-
h = altura do paralelogramo, ou seja, a distância entre a base e seu lado oposto.
Exemplos:
Calcule a área de um paralelogramo cuja base é igual a 13 cm e a altura é igual a 22 cm.
AP = b·h
AP = 13·22
AP = 286 cm2
Calcule a altura de um paralelogramo cuja área é igual a 121 cm2 e a base mede 11 cm.
AP = b·h
121 = 11·h
121 = h
11
11 = h
Logo, a altura é 11 cm.
Área do retângulo
Os retângulos são paralelogramos que possuem os quatro ângulos retos. Dessa maneira, os retângulos herdam todas as características e propriedades dos paralelogramos, inclusive a área.
OBS.: Todo retângulo é um paralelogramo, mas nem todo paralelogramo é um retângulo.
Dessa maneira, a área do retângulo é igual à área do paralelogramo:
AP = b·h
.jpg "Retângulo")
Exemplo de retângulo com destaque para as medidas b e h
Área do quadrado
Um quadrado é um retângulo que possui todos os lados congruentes. Para mais informações a respeito dos quadrados, clique aqui.
O quadrado também é um paralelogramo, portanto, a área do paralelogramo vale para o quadrado. É comum que as questões sobre essa figura só evidenciem um de seus lados. Para calcular a área, basta lembrar que todos os lados são iguais e substituir b e h pelo mesmo valor.
.jpg "Quadrado")
Exemplos:
Calcule a área de um quadrado que possui lado igual a 9 cm.
AP = b·h
AP = 9·9
AP = 81 cm2
Calcule o lado de um quadrado cuja área mede 25 cm2.
AP = b·h
Como os dois lados possuem a mesma medida, podemos escrever:
AP = b·b
AP = b2
25 = b2
Fazendo a raiz quadrada em ambos os membros da equação, teremos:
5 = b
O lado do quadrado é igual a 5 cm.
Observe que, como os lados (l) do quadrado são congruentes, questões sobre sua área sempre envolverão uma multiplicação do comprimento do lado por ele mesmo. Sendo essa a definição de potenciação, podemos escrever a área do quadrado (AQ) da seguinte forma:
AQ = l·l
AQ = l2
Área do losango
Os losangos são paralelogramos que possuem todos os lados congruentes. Não os confunda com os quadrados, que, além de congruentes, também possuem todos os ângulos iguais a 90°.
A área do losango não é calculada a partir de sua base e altura. São necessários os comprimentos de suas duas diagonais para isso. Sendo assim, dadas as diagonais D e d de um losango, sua área (AL) pode ser encontrada pela fórmula:
AL = D·d
2
.jpg "Losango")
Exemplos:
Calcule a área de um losango cuja diagonal maior mede 5 cm e a diagonal menor mede 4 cm.
AL = D·d
2
AL = 5·4
2
AL = 20
2
AL = 10 cm2
Por Luiz Paulo Moreira
Graduado em Matemática
