A classificação dos polígonos é utilizada para nomeá-los. Por exemplo, quando o polígono possui exatamente três ângulos, ele é chamado de triângulo; quando ele possui quatro ângulos, ele é chamado de quadrilátero. Acima de quatro lados, os polígonos são nomeados como pentágonos, hexágonos e assim sucessivamente.
É possível classificar os polígonos também de acordo com a medida de seus lados e também de seus ângulos. Com relação aos lados, um polígono pode ser regular, quando possui lados e ângulos congruentes, ou irregular. Quanto aos ângulos, ele pode ser classificado como convexo, quando todos os seus ângulos são menores que 180º, ou côncavo (não convexo), quando possui pelo menos um ângulo maior que 180º.
Leia também: Classificação dos triângulos – critérios e nomenclatura
Tópicos deste artigo
Classificação dos polígonos
Um polígono pode ser classificado de acordo com as suas características. Uma delas é o número de lados ou de ângulos. Além dessa classificação, um polígono pode ser tido como regular ou irregular, de acordo com a medida dos seus ângulos e a congruência ou não de seus lados. Uma terceira classificação dos polígonos leva em consideração o tamanho de seus ângulos internos. Quando um deles é um ângulo maior que 180º, esse polígono é conhecido como não convexo ou côncavo.

-
Quanto ao número de lados ou ângulos
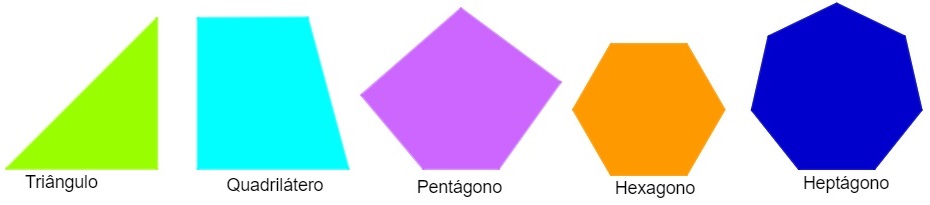
Para reconhecer e nomear um polígono, levamos em consideração a quantidade de lados ou a quantidade de ângulos que ele possui, que são, inclusive, iguais. Os polígonos com menor número de lados são o triângulo (três ângulos) e o quadrilátero (quatro lados). A partir de um polígono de cinco lados, existe um padrão na construção dos nomes desses polígonos: apresentamos as quantidades com o prefixo grego correspondente ao número de lados mais o sufixo -gono.
A utilização das quantidades em grego é bastante comum na matemática e na química. Os prefixos mais comuns são:
Penta → cinco
Hexa → seis
Hepta → sete
Octa → oito
Enea → nove
Deca → dez
Hendeca ou undeca → onze
Dodeca → doze
Icosa→ vinte
Sendo assim, ao juntarmos a quantidade de lados em grego com a terminação -gono (que significa ângulo), vamos encontrar:
Pentágono → polígono de 5 lados
Hexágono → polígono de 6 lados
Heptágono → polígono de 7 lados
Octágono → polígono de 8 lados
Eneágono → polígono de 9 lados
Decágono → polígono de 10 lados
Undecágono ou hendecágono → polígono de 11 lados
Dodecágono → polígono de 12 lados
Icoságono → polígono de 20 lados
Muitas vezes o universo bidimensional é confundido com o tridimensional, que não utiliza a terminação gono (que faz menção ao ângulo), mas sim a terminação -edro (que faz menção às faces), o que ocorre com os sólidos geométricos, como icosaedro, dodecaedro, entre outros, que são tridimensionais e conhecidos como poliedros.
Veja também: Diferenças entre figuras planas e espaciais
-
Polígono regular e irregular
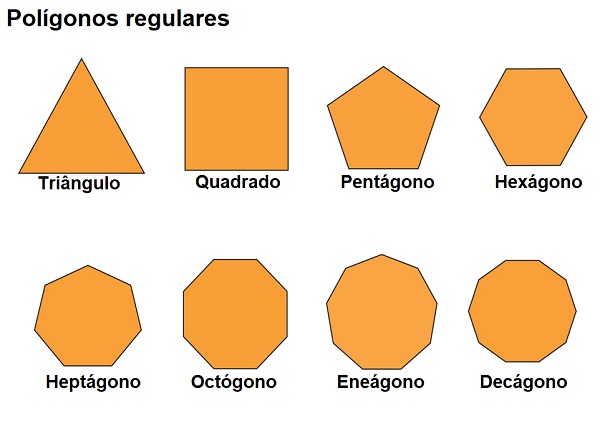
Um polígono pode ser classificado como regular quando ele possui todas os ângulos e lados congruentes. Ser congruente significa possuir a mesma medida. O triângulo equilátero e o quadrado são exemplos. Quando pelo menos um dos lados é diferente, o polígono é irregular.
O termo equilátero é usado em referência a lados iguais. Aplica-se o mesmo raciocínio para os ângulos, surgindo o termo equiângulo.
-
Polígonos convexos e não convexos
Existem várias formas de explicar o que seria um polígono convexo e um polígono não convexo. De forma geométrica, podemos afirmar que um polígono é convexo quando, ao escolhermos dois pontos A e B quaisquer, o segmento de reta que une esses dois pontos está contido no polígono. Caso contrário, ou seja, se existir pelo menos dois pontos contidos no polígono cujo segmento de reta que os liga não está contido no polígono, ele é conhecido como não convexo ou côncavo.

Uma forma bastante fácil de identificar é analisando os ângulos internos do polígono. Quando ele possui um ângulo maior que 180º, ele será, consequentemente, um polígono não convexo.
Acesse também: Paralelogramos – polígonos que possuem lados opostos paralelos
Exercícios resolvidos
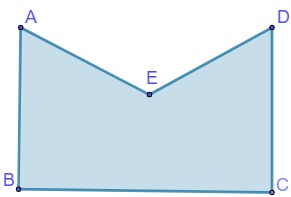
Questão 1 - Analisando o polígono a seguir, podemos classificá-lo como:
A) hexágono, convexo e regular.
B) hexágono, não convexo e irregular.
C) pentágono, convexo e regular.
D) pentágono, côncavo e irregular.
E) quadrilátero, convexo e regular.
Resolução
Alternativa D. Analisando a figura, podemos afirmar que ele possui cinco lados, logo é um pentágono. Ele possui um ângulo AÊD maior que 180º, o que faz com que ele seja também côncavo, ou seja, não convexo. Por fim, os ângulos não são todos iguais, o que o torna irregular, então ele é um pentágono côncavo e irregular.
Questão 2 - Sobre as classificações de polígono, julgue as afirmativas a seguir:
I – Todo triângulo é convexo.
II – Definimos como polígono regular aquele que possui todos os ângulos congruentes.
III – Todo polígono convexo é regular.
Podemos afirmar que:
A) somente I é verdadeira.
B) somente II é verdadeira.
C) somente III é verdadeira.
D) somente I e II são verdadeiras.
E) somente II e II são verdadeiras.
Resolução
Alternativa A.
→ 1º passo: julgar as afirmativas.
I – Todo triângulo é convexo.
Verdadeira, pois os ângulos internos do triângulo são sempre menores que 180º, já que a soma dos três ângulos é igual a 180º.
II – Definimos como polígono regular aquele que possui todos os ângulos congruentes.
Falsa, pois não só os ângulos mas também os lados precisam ser congruentes. O retângulo é um exemplo de polígono não regular que possui ângulos congruentes.
III – Todo polígono convexo é regular.
Falsa. Para ser convexo, basta ter ângulos menores que 180º, o que não quer dizer que ele precisa ter lados e ângulos congruentes.
→ 2º passo: analisar as alternativas.
Somente a I é verdadeira.
Por Raul Rodrigues de Oliveira
Professor de Matemática






