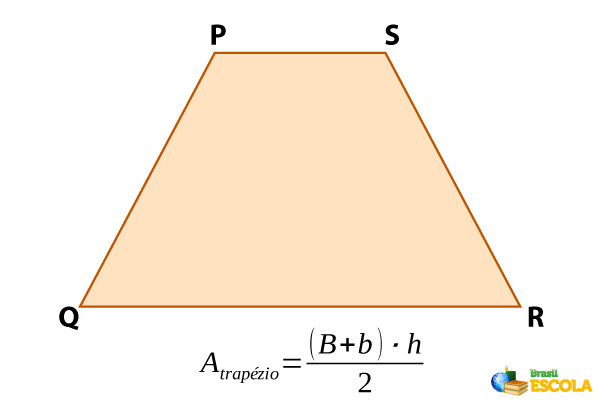
A área do trapézio é a medida de sua região interna, delimitada pelos segmentos que o compõem: duas bases paralelas e duas laterais. Podemos encontrar a área de um trapézio ao calcular a metade do produto entre sua altura e a soma de suas bases.
Veja também: Área do cubo — como calcular?
Tópicos deste artigo
- 1 - Resumo sobre área do trapézio
- 2 - O que é trapézio?
- 3 - Qual é a fórmula da área do trapézio?
- 4 - Como calcular a área do trapézio?
- 5 - Classificação do trapézio
- 6 - Perímetro do trapézio
- 7 - Exercícios resolvidos sobre área do trapézio
Resumo sobre área do trapézio
- Trapézio é um quadrilátero formado por dois segmentos paralelos chamados de bases e dois segmentos oblíquos chamados de laterais.
- A área de um trapézio é dada pela metade do produto entre sua altura e a soma de suas bases. Em símbolos matemáticos, a fórmula da área do trapézio é:
\(Área_{trapézio} =\frac{\left(B+b\right)\cdot h}{2}\)
- Trapézios são classificados em isósceles (se possuem laterais congruentes), retângulos (se uma das laterais forma ângulos retos com as bases) e escalenos (se não forem isósceles nem retângulos).
- O perímetro de um trapézio é a soma das medidas de seus quatro segmentos, ou seja, a soma das bases e das laterais.
O que é trapézio?
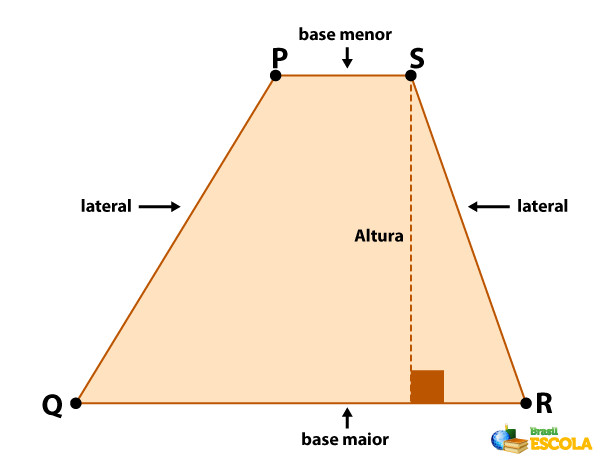
Um trapézio é um quadrilátero (polígono de quatro lados) que possui dois lados paralelos e dois lados oblíquos. Os lados paralelos são chamados de bases (base menor e base maior) e os lados oblíquos são chamados de laterais. A altura do trapézio é a distância entre as bases.
Qual é a fórmula da área do trapézio?
A fórmula da área de um trapézio é:
\(Área_{trapézio} =\frac{\left(B+b\right)\cdot h}{2}\)
- B → base maior do trapézio
- b → base menor do trapézio
- h → altura do trapézio
→ Demonstração da fórmula da área do trapézio
Vamos considerar PQRS um trapézio com base menor PS medindo b e base maior QR medindo B, como na imagem abaixo. A altura do trapézio tem medida h.
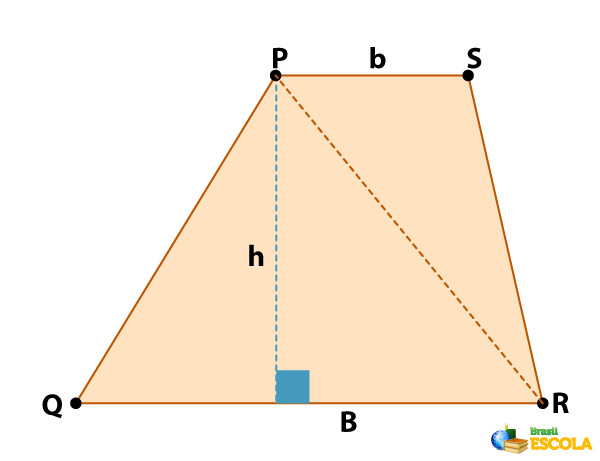
Observe que podemos repartir o trapézio PQRS em dois triângulos: PQR e PRS. Assim, a área do trapézio PQRS é igual à soma das áreas dos triângulos.
\(Área_{PQRS}=Área_{PQR}+Área_{PRS}\)
Como OS é paralelo a QR, a altura do trapézio também é a altura dos triângulos PQR e PRS, logo, a área do trapézio PQRS é dada por:
\(Área_{PQRS}= \frac{B⋅h} 2 + \frac{b⋅h} 2\)
\(Área_{PQRS} =\frac{\left(B+b\right)\cdot h}{2}\)
Como calcular a área do trapézio?
Calculamos a área do trapézio por meio de sua fórmula. Veja um exemplo de cálculo a seguir.
Exemplo:
Considere um trapézio com bases de 4 cm e 12 cm e altura medindo 5 cm. Qual a área desse trapézio?
Resolução:
Segundo o enunciado, a base menor (b) mede 4 cm, a base maior (B) mede 12 cm e a altura (h) mede 5 cm. Portanto, basta substituir essas informações na fórmula da área do trapézio:
\(Área_{trapézio} =\frac{\left(B+b\right)\cdot h}{2}\)
\(Área_{trapézio} =\frac{\left(12+4\right)\cdot 5}{2}\)
\(Área_{trapézio} = \frac{16⋅5}2\)
\(Área_{trapézio}=40 cm^2\)
Veja também: Área da pirâmide — como calcular?
Classificação do trapézio
Podemos classificar um trapézio em três tipos:
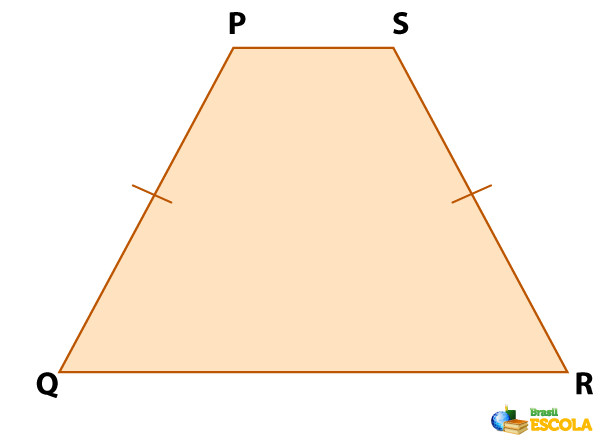
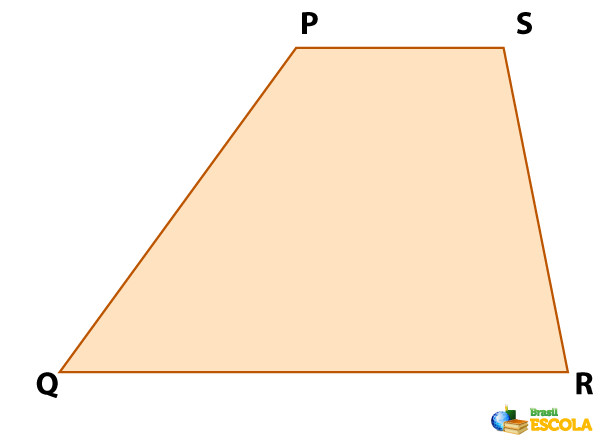
- Trapézio isósceles: quando as laterais são congruentes (de mesma medida).
- Trapézio retângulo: quando uma lateral forma ângulos retos com as bases.
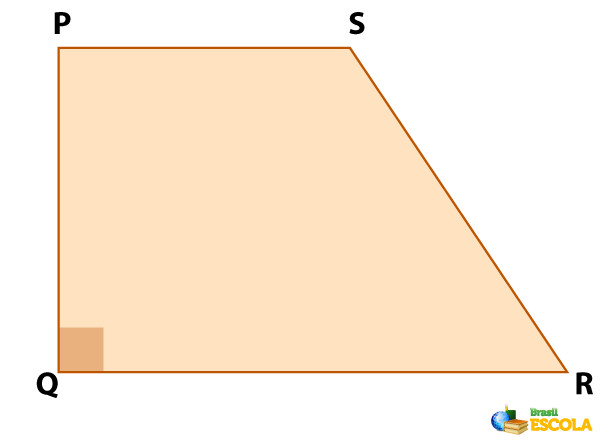
- Trapézio escaleno: nos demais casos, ou seja, quando não for isósceles nem retângulo.
Perímetro do trapézio
O perímetro de um polígono é a medida da soma de seus lados. No caso do trapézio, o perímetro é a soma de seus quatro segmentos, as duas bases e as duas laterais.
Exemplo:
Determine o perímetro de um trapézio com base menor medindo 3 cm, base maior medindo 12 cm e laterais medindo 8,64 cm e 10 cm.
Resolução:
Como o perímetro do trapézio é a soma de seus lados, o trapézio descrito possui:
\(3+12+8,54+10=33,54\ cm\)
Exercícios resolvidos sobre área do trapézio
Questão 1
Um trapézio possui área de 20 cm2, base menor de 2 cm e base maior de 8 cm. A altura desse trapézio é:
A) 4 cm
B) 10 cm
C) 16 cm
D) 30 cm
E) 64 cm
Resolução:
Alternativa A
Como o cálculo da área de um trapézio envolve as medidas das bases e da altura, podemos substituir diretamente os dados do enunciado na fórmula:
\(Área_{trapézio} =\frac{\left(B+b\right)\cdot h}{2}\)
\(20=\frac{\left(8+2\right)\cdot h}{2}\)
\(20=5\cdot h\)
\(h=4\ cm\)
Questão 2
(Unesp – adaptado) A figura representa um triângulo retângulo de vértices A, B e C, em que o segmento de reta DE é paralelo ao lado AB do triângulo.
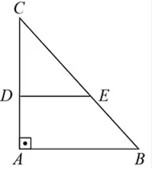
Se AB = 15 cm, DE = 9 cm e AD = 8 cm, a área de ABED, em cm², é:
A) 84
B) 96
C) 120
D) 150
E) 192
Resolução:
Alternativa B
Como o segmento DE é paralelo ao segmento AB, o quadrilátero ABED é um trapézio (em particular, um trapézio retângulo, pois possui um ângulo reto em A).
Perceba que AB é a base maior, DE a base menor e AD é a altura (além de ser uma das laterais do trapézio). Portanto, podemos determinar a área do trapézio ABED:
\(Área_{trapézio} =\frac{\left(B+b\right)\cdot h}{2}\)
\(Área_{trapézio} =\frac{\left(15+9\right)\cdot 8}{2}\)
\(Área_{trapézio}=96 cm^2\)
Por Maria Luiza Alves Rizzo
Professora de Matemática