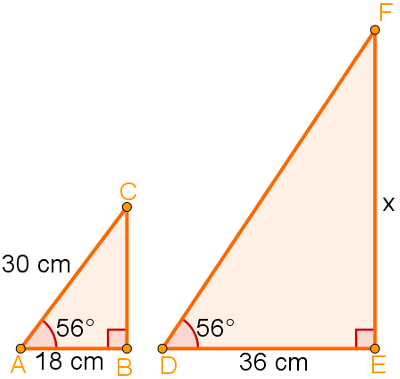
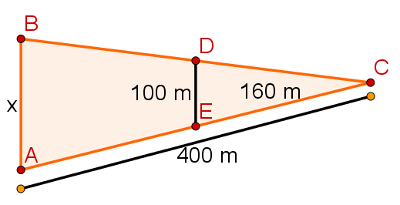
Quando comparamos duas figuras geralmente queremos saber quais as semelhanças existentes entre elas. Algumas vezes elas são iguais, algumas vezes são apenas parecidas e também existem os casos em que as figuras comparadas são completamente diferentes. Na matemática, frequentemente as figuras geométricas são comparadas e os resultados possíveis são: Figuras congruentes, figuras semelhantes e figuras diferentes. A seguir, discutiremos a semelhança entre polígonos e os casos de semelhança entre triângulos.
Dois polígonos são semelhantes quando existe proporcionalidade entre seus lados e seus ângulos correspondentes são todos iguais. Existir uma razão de proporcionalidade quer dizer que se dividirmos a medida de um lado da primeira figura pelo valor de um lado da segunda figura e o resultado for, por exemplo, o número 3, então todas as divisões entre medidas de lados da primeira figura por medidas dos lados da segunda figura terão 3 como resultado.
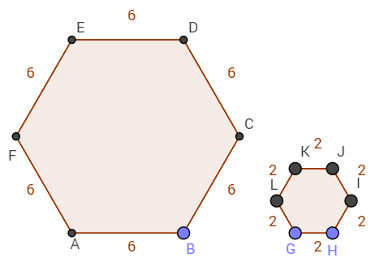
Isso ocorre no caso dos hexágonos da imagem acima. Repare que a divisão de qualquer lado do primeiro hexágono por qualquer lado do segundo tem 3 como resultado.
Para que dois polígonos sejam semelhantes, deve existir proporcionalidade entre seus lados correspondentes, além de ângulos correspondentes congruentes.
Voltando ao exemplo dos hexágonos acima, observe que a razão entre lados correspondentes é sempre 3:
AB = BC = CD = DE = EF = FA = 3
GH HI IJ JK KL LG
Para mostrar que eles são semelhantes, falta apenas mostrar que seus ângulos correspondentes são congruentes. Nesse caso são, por terem sido construídos como polígonos regulares.
Para os triângulos a regra é a mesma. Dois triângulos são semelhantes caso três ângulos correspondentes sejam congruentes e 3 lados correspondentes possuam a mesma razão de proporcionalidade.
Porém, é possível verificar a semelhança nos triângulos de uma forma mais simples. Basta observar se eles se enquadram em um dos casos de semelhança de triângulos a seguir:
1- Caso Ângulo Ângulo (AA): Dois triângulos são semelhantes se possuírem dois ângulos correspondentes congruentes.
Não é necessário verificar o terceiro ângulo e nenhuma proporcionalidade entre os lados. Basta que dois ângulos sejam congruentes e os dois triângulos já podem ser declarados semelhantes, como no exemplo a seguir:
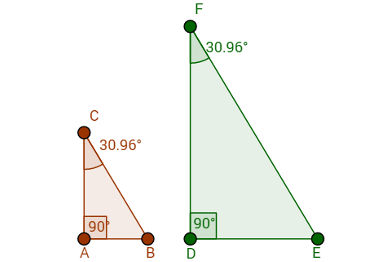
2- Caso Lado Lado Lado (LLL): Se dois triângulos possuem três lados proporcionais, então esses dois triângulos são semelhantes. Portanto, não é necessário verificar os ângulos.
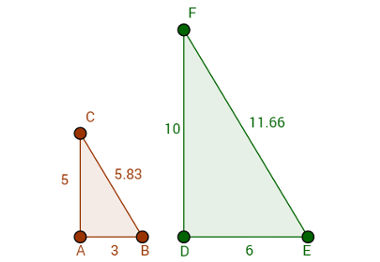
Na imagem acima, observe que as razões entre lados correspondentes têm o mesmo resultado:
AB = BC = CA = 1
DE EF FD 2
Então, pelo segundo caso de semelhança, esses triângulos são semelhantes.
3- Caso Lado Ângulo Lado (LAL): Dois triângulos que possuem dois lados proporcionais e o ângulo entre eles congruente são semelhantes. Observe este caso de semelhança no exemplo:
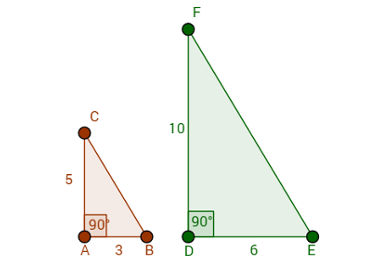
AB = CA = 1
DE FD 2
Nesse exemplo, o ângulo de 90 graus fica entre os lados proporcionais. Configurando assim o caso LAL.
Por Luiz Paulo Moreira
Graduado em Matemática