Você sabe como calcular a área da figura acima? Provavelmente quando você aprendeu a calcular áreas de figuras geométricas, não deve ter aprendido nenhuma fórmula para calcular a área de uma casinha! Mas nós podemos adaptar essa figura para deixá-la com uma forma mais comum e fácil de trabalhar. Essa casinha foi formada por peças do tangram, um antigo quebra-cabeça chinês. Se reorganizarmos as peças do tangram, podemos formar mais de 1000 figuras, mas, sem dúvidas, o formato mais simples para calcular a área é a imagem a seguir:
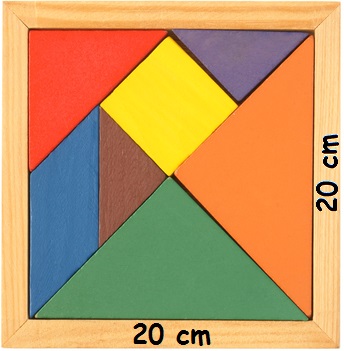
Esse quadrado corresponde a figura anterior, a área de ambas são iguais
Na imagem acima há um quadrado formado exatamente com as mesmas peças que compunham a casinha. Portanto, a área das duas figuras será a mesma. Vamos então calcular a área das figuras, utilizando o último desenho. Para calcularmos a área de um quadrado, devemos fazer:
Área = lado x lado
Área = 20 cm x 20 cm
Área = 400 cm²
Então a área da casinha, assim como a área de qualquer outra figura formada por esse tangram, sempre será 400 cm². Todas as figuras que podem ser formadas através do tangram podem ser chamadas de figuras equidecomponíveis, pois são formas aparentemente distintas, mas que possuem uma mesma área. Utilizando essa ideia, podemos calcular várias formas geométricas, por exemplo:
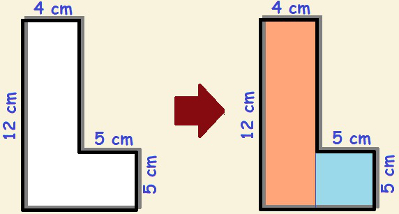
Você conhece uma forma de calcular a área desse polígono côncavo em formato de “L”
Todos os polígonos, sejam eles côncavos ou convexos, são figuras equidecomponíveis. Na figura acima, temos um polígono côncavo, cuja forma assemelha-se a um “L”. Para calcularmos a área dessa figura, podemos decompô-la em duas formas conhecidas, um quadrado e um retângulo. Na figura, destacamos o quadrado com a cor azul e o retângulo com a cor laranja, vamos então calcular sua área:
Área total = área do retângulo + área do quadrado
Área total = (base x altura) + (lado x lado)
Área total = (4 cm x 12 cm) + (5 cm x 5 cm)
Área total = (48 cm²) + (25 cm²)
Área total = 73 cm²
Portanto, a área do polígono em formato de “L” é 73 cm². Partindo desse princípio das áreas das figuras equidecomponíveis, através da decomposição, podemos calcular a área de polígonos sem precisar decorar fórmulas e mais fórmulas. Vejamos nas imagens a seguir alternativas para o cálculo de algumas áreas:
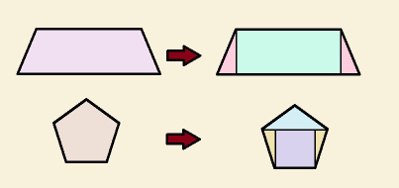
Todos os polígonos podem ser decompostos em figuras equidecomponíveis
Para obtermos a área do trapézio, basta decompô-lo em um retângulo e dois triângulos para que calculemos a área de cada uma dessas formas. O pentágono foi decomposto em três triângulos e um quadrado, mas poderia ter sido decomposto em três triângulos, por exemplo, ou em qualquer outra forma que facilitasse o cálculo.
Por Amanda Gonçalves
Graduada em Matemática
