Área do losango

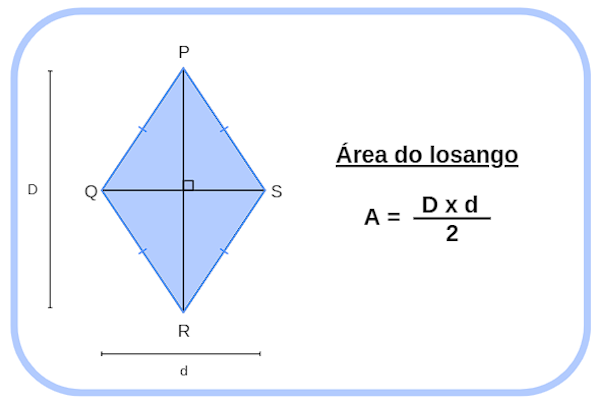
A área do losango é a medida de sua região interna. Uma maneira de calcular a área de um losango é determinar a metade do produto entre a diagonal maior e a diagonal menor, cujas medidas são representadas por D e d respectivamente.

Leia também: Como calcular a área de um quadrado?

Tópicos deste artigo

• 1 - Resumo sobre a área do losango
• 2 - Elementos do losango
• 3 - Propriedades das diagonais do losango
• 4 - Fórmula da área do losango
• 5 - Como calcular a área de um losango?
• 6 - Exercícios sobre a área do losango

Resumo sobre a área do losango

• O losango é um paralelogramo de quatro lados congruentes e ângulos opostos congruentes.

• As duas diagonais de um losango são conhecidas como diagonal maior (D) e diagonal menor (d).

• Cada diagonal de um losango divide esse polígono em dois triângulos congruentes.

• As duas diagonais do losango são perpendiculares e se cruzam em seus pontos médios.

• A fórmula para calcular a área do losango é:

\(A=\frac{D\times d}{2}\)

Elementos do losango

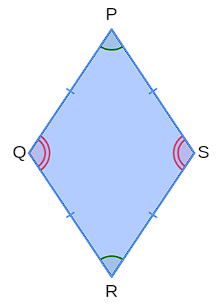
O losango é um paralelogramo formado por quatro lados de tamanhos iguais e ângulos opostos de mesma medida. No losango abaixo, temos que \(\overline{PQ}=\overline{QR}=\overline{RS}=\overline{SP}\), \(\hat{P}=\hat{R}\) e \(\hat{Q}=\hat{S}\).

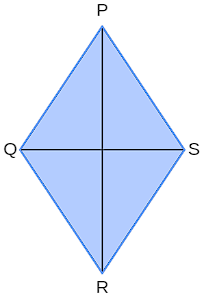
Os segmentos com extremidades em vértices opostos são as diagonais do losango. Na imagem abaixo, chamamos o segmento \(\overline{PR}\) de diagonal maior e o segmento \(\overline{QS}\) de diagonal menor.

Propriedades das diagonais do losango

Vamos conhecer duas propriedades relacionadas às diagonais do losango.

• Propriedade 1: Cada diagonal divide o losango em dois triângulos isósceles congruentes.

 Primeiro considere a diagonal maior \(\overline{PR}\) de um losango PQRS de lado l.

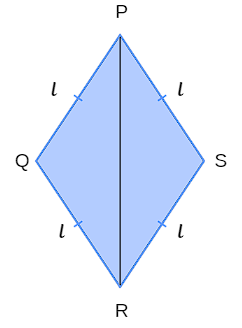
Perceba que \(\overline{PR}\) divide o losango em dois triângulos: PQR e PSR. Ainda:

\(\overline{PQ}=\overline{PS}=l\)

\(\overline{QR}=\overline{SR}=l\)

\(\overline{PR}\) é lado comum.

Assim, pelo critério LLL, os triângulos PQR e PSR são congruentes.

Agora considere a diagonal menor \(\overline{QS}\).

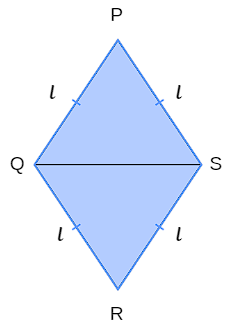
Perceba que \(\overline{QS} \) divide o losango em dois triângulos: PQS e RQS. Ainda:

\(\overline{PQ}=\overline{RQ}=l\)

\(\overline{PS}=\overline{RS}=l\)

\(\overline{QS}\) é lado comum.

Assim, pelo critério LLL, os triângulos PQS e RQS são congruentes.

• Propriedade 2: As diagonais de um losango são perpendiculares e se cruzam no ponto médio de cada uma.

O ângulo formado pelas diagonais \(\overline{PR}\) e \(\overline{QS}\) mede 90°.

Seja O o ponto de encontro das diagonais \(\overline{{PR}}\) e \(\overline{{QS}}\); assim, O é ponto médio de \(\overline{PR}\) e também é ponto médio de \(\overline{QS}\). Se \( \overline{PR}\) mede D e \(\overline{QS}\) mede d, isso significa que:

\(\overline{PO}=\overline{OR}=\frac{D}{2}\)

\(\overline{QO}=\overline{OS}=\frac{d}{2}\)

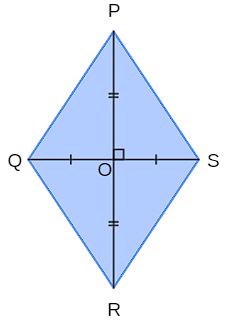
Observação: As duas diagonais de um losango dividem essa figura em quatro triângulos retângulos congruentes. Considere os triângulos PQO, RQO, PSO e RSO. Note que cada um possui um lado de medida l (a hipotenusa), um de medida \(\frac{D}{2}\) e outro de medida \(\frac{d}{2}\).

Veja também: Comparação e semelhança entre triângulos

Fórmula da área do losango

Seja D a medida da diagonal maior e d a medida da diagonal menor de um losango; a fórmula da área do losango é:

\(A=\frac{D\times d}{2}\)

Vejamos, a seguir, a demonstração dessa fórmula.

De acordo com a primeira propriedade que estudamos neste texto, a diagonal \(\overline{QS}\) divide o losango PQRS em dois triângulos congruentes (PQS e RQS). Isso significa que esses dois triângulos possuem a mesma área. Consequentemente, a área do losango é o dobro da área de um desses triângulos.

\(A_{\mathrm{losango}}=2\times A_{triângulo} PQS\)

Conforme a segunda propriedade que estudamos, a base do triângulo PQS mede d e a altura mede D2. Lembre-se de que a área de um triângulo pode ser calculada por  base×altura2. Logo:

\(A_{\mathrm{losango}}=2\times A_{triângulo} PQS\)

\(A_{\mathrm{losango}}=2\times\left(\frac{d\times\frac{D}{2}}{2}\right)\)

\(A_{\mathrm{losango}}=2\times\left(\frac{d\times\frac{D}{2}}{2}\right)\)

\(A_{\mathrm{losango}}=\frac{D\times d}{2}\)

Como calcular a área de um losango?

Como vimos, caso as medidas das diagonais sejam informadas, basta aplicar a fórmula para calcular a área de um losango:

\(A=\frac{D\times d}{2}\)

Do contrário, precisamos adotar outras estratégias, considerando, por exemplo, as propriedades desse polígono.

Exemplo 1: Qual a área de losango cujas diagonais medem 2 cm e 3 cm?

Aplicando a fórmula, temos que:

\(A_{\mathrm{losango}}=\frac{D\times d}{2}\)

\(A_{\mathrm{losango}}=\frac{3\times2}{2}\)

\(A_{\mathrm{losango}}=3 cm²\)

Exemplo 2: Qual a área de losango cujo lado e a diagonal menor medem, respectivamente, 13 cm e 4 cm?

Pela observação da propriedade 2, as diagonais de um losango dividem esse polígono em quatro triângulos retângulos congruentes. Cada triângulo retângulo possui catetos de medida \(\frac{d}{2}\) e \(\frac{D}{2}\) e hipotenusa de medida l. Pelo teorema de Pitágoras:

\(l^2=\left(\frac{d}{2}\right)^2+\left(\frac{D}{2}\right)^2\)

Substituindo \(d=4 cm\) e d=4 cm, temos que

\(\left(\sqrt{13}\right)^2=\left(\frac{4}{2}\right)^2+\left(\frac{D}{2}\right)^2\)

\(13=4+\frac{D^2}{4}\)

\(D^2=36\)

Como D é a medida de um segmento, podemos considerar apenas o resultado positivo. Ou seja:

D=6

Aplicando a fórmula, temos que:

\(A_{\mathrm{losango}}=\frac{D\times d}{2}\)

\(A_{\mathrm{losango}}=\frac{6\times4}{2}\)

\(A_{\mathrm{losango}}=\ 12 cm²\)

Saiba mais: Fórmulas usadas para calcular a área das figuras planas

Exercícios sobre a área do losango

Questão 1

(Fauel) Em um losango, as diagonais medem 13 e 16 cm. Qual é a medida de sua área?

a) 52 cm²

b) 58 cm²

c) 104 cm²

d) 208 cm²

e) 580 cm²

Resolução: alternativa C

Aplicando a fórmula, temos que:

\(A_{\mathrm{losango}}=\frac{D\times d}{2}\)

\(A_{\mathrm{losango}}=\frac{16\times13}{2}\)

\(A_{\mathrm{losango}}=\ 104 cm²\)

Questão 2

(Fepese) Um fábrica produz peças de cerâmica no formato de um losango, cuja diagonal menor mede um quarto da diagonal maior e a diagonal maior mede 84 cm.

Logo, a área de cada peça de cerâmica produzida por esta fábrica, em metros quadrados, é:

a) maior que 0,5.

b) maior que 0,2 e menor que 0,5.

c) maior que 0,09 e menor que 0,2.

d) maior que 0,07 e menor que 0,09.

e) menor que 0,07.

Resolução: alternativa D

Se D é a diagonal maior e d é a diagonal menor, então:

\(d=\frac{1}{4}D\)

\(d=\frac{1}{4}\cdot84\)

\(d=21 cm\)

Aplicando a fórmula, temos que

\(A_{\mathrm{losango}}=\frac{D\times d}{2}\)

\(A_{\mathrm{losango}}=\frac{84\times21}{2}\)

\(A_{\mathrm{losango}}=882 cm²\)

Como 1 cm² corresponde a \(1\cdot{10}^{-4} m²\), então:

\(\frac{1\ cm^2}{882\ cm^2}=\frac{1\cdot{10}^{-4}\ m^2}{x}\)

\(x=0,0882 m²\)

 

Por Maria Luiza Alves Rizzo
Professora de Matemática