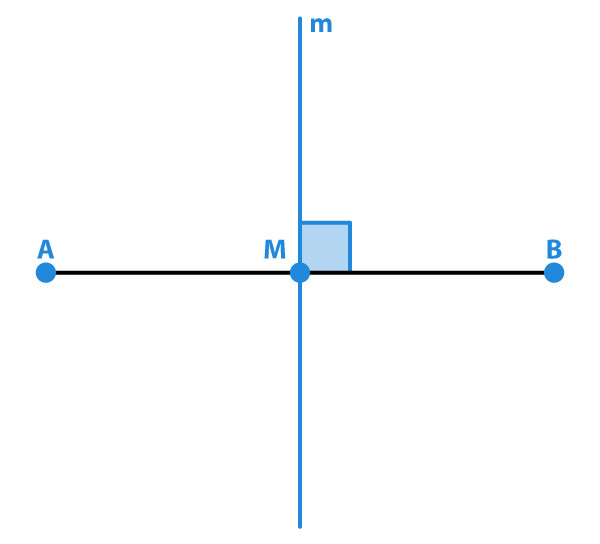
Mediatriz

Mediatriz é a reta perpendicular a um segmento que intercepta seu ponto médio. Podemos construir a mediatriz de um segmento utilizando régua e compasso. Em um triângulo, as mediatrizes são retas perpendiculares aos lados que contêm seus pontos médios. Assim, um triângulo possui três mediatrizes. O ponto de encontro dessas mediatrizes é chamado de circuncentro e constitui o centro da circunferência circunscrita ao triângulo.

Leia também: Distância entre dois pontos — o menor caminho entre dois pontos no plano cartesiano

Tópicos deste artigo

• 1 - Resumo sobre mediatriz
• 2 - O que é mediatriz?
• 3 - Como construir a mediatriz?
• 4 - Como encontrar a equação da mediatriz?
• 5 - Mediatriz de um triângulo
• 6 - Diferenças entre mediatriz, mediana, bissetriz e altura de um triângulo
• 7 - Exercícios resolvidos sobre mediatriz

Resumo sobre mediatriz

• Mediatriz é a reta perpendicular a um segmento passando pelo ponto médio.

• Os pontos de uma mediatriz são equidistantes das extremidades do segmento.

• A mediatriz pode ser construída com régua e compasso.

• A equação de uma mediatriz pode ser determinada com base nas coordenadas das extremidades do segmento.

• Um triângulo possui três mediatrizes, uma em relação a cada lado.

• O ponto de interseção das mediatrizes de um triângulo é chamado de circuncentro. Esse ponto é o centro da circunferência circunscrita ao triângulo.

• A mediatriz de um triângulo se difere da mediana, da bissetriz e da altura de um triângulo.

O que é mediatriz?

Dado um segmento, a mediatriz é a reta perpendicular ao segmento que intercepta seu ponto médio.

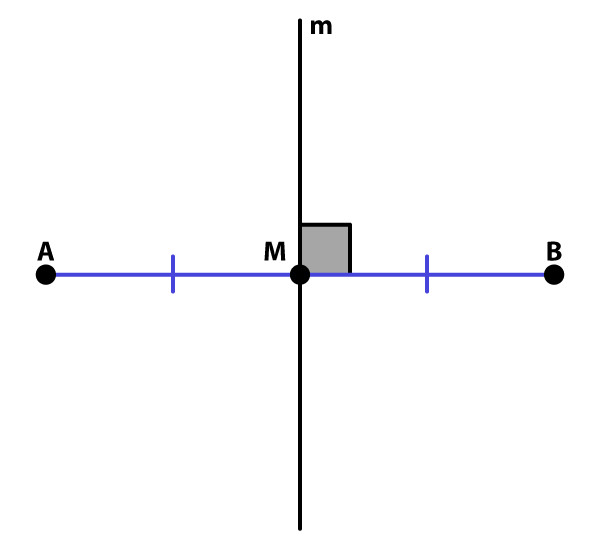
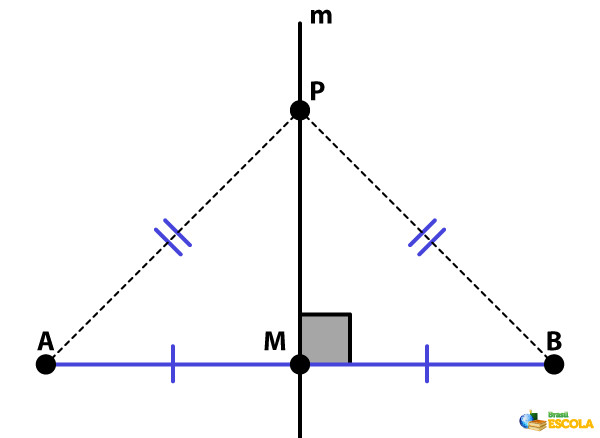
Uma consequência importante dessa definição é que todos os pontos sobre uma mediatriz estão à mesma distância das extremidades do segmento. Em simbologia matemática, se AB é um segmento e o ponto P pertence à mediatriz, então PA = PB.

Como construir a mediatriz?

Para construir a mediatriz de um segmento, precisamos somente de régua e compasso. Os passos para a construção são os seguintes:

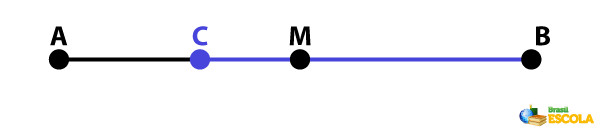
• Passo 1: Dado um segmento AB, abra o compasso com um comprimento maior que a metade do segmento. Dica: uma possibilidade é utilizar o próprio comprimento do segmento.

• Passo 2: Desenhe uma circunferência com centro em uma das extremidades do segmento e raio com a medida escolhida no passo 1.

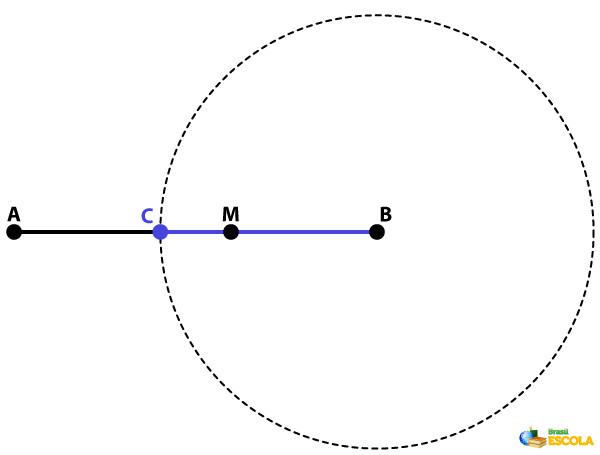
• Passo 3: Repita o passo 2 para a outra extremidade do segmento.

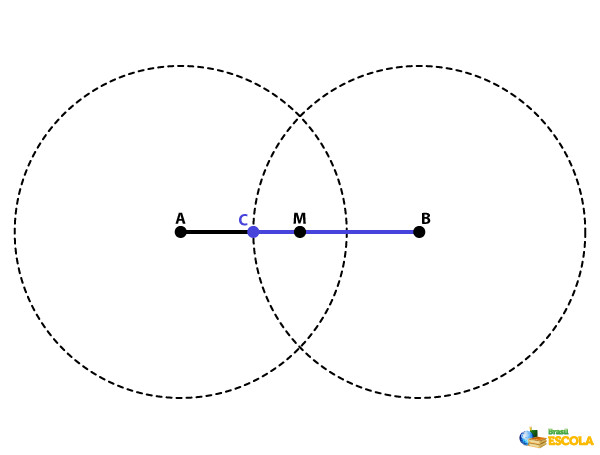
• Passo 4: Una com a régua os pontos de interseção das circunferências.

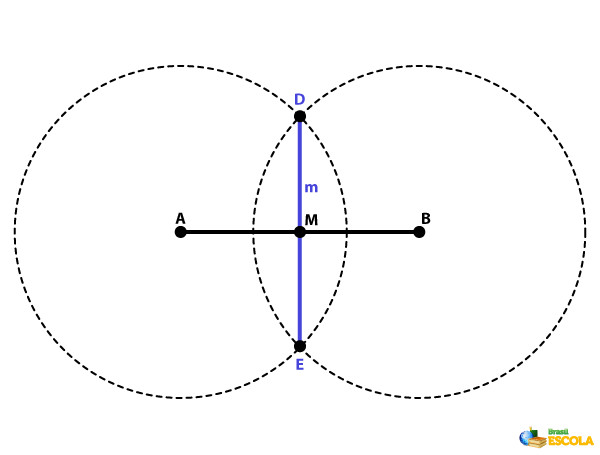
Como encontrar a equação da mediatriz?

Como a mediatriz é uma reta, podemos determinar uma equação que descreva seus pontos, sendo r a reta que contém um segmento AB dado, s a reta mediatriz desse segmento e P (x,y) um ponto qualquer sobre a mediatriz.

Supondo que as coordenadas dos pontos A e B sejam conhecidas, podemos obter o coeficiente angular n da reta r. Como r e s são perpendiculares, o coeficiente angular m da reta s (a mediatriz) também pode ser encontrado, pois é o oposto do inverso multiplicativo de n. Utilizando a expressão para a equação fundamental da reta, \(y-y_0=m(x-x_0 )\), em que \(M(x\_0,y\_0)\) é o ponto médio de AB, concluímos a equação da mediatriz.

• Exemplo:

Determine a equação da mediatriz do segmento determinado pelos pontos A(1,2) e B(3,6).

Resolução:

Primeiramente, vamos obter o coeficiente angular n da reta r que contém o segmento AB:

\(n_r=\frac{Δ y}{Δ x}=\frac{6-2}{3-1}=\frac{4}2 =2\)

Agora, buscamos o ponto médio M do segmento AB:

\(M(x_0,y_0 )=M(\frac{1+3}{2},\frac{2+6}{2})=M(2,4)\)

Lembre-se de que a mediatriz s procurada é perpendicular à reta r (que contém o segmento AB). Logo, o coeficiente angular m da reta s e o coeficiente angular n da reta r se relacionam da seguinte forma:

\(m_s=\frac{-1}{n_r} \)

Portanto, \( m_s=\frac{-1}2\).

Por fim, utilizamos a equação fundamental da reta para determinar a mediatriz s, uma reta que possui coeficiente angular igual a \(-\frac{1}2\) e passa pelo ponto (2,4):

\(y-y_0=m\cdot(x-x_0 )\)

\(y-4=-\frac{1}2\cdot(x-2)\)

\(y=-\frac{1}2 x+5\)

Mediatriz de um triângulo

Os três lados de um triângulo são segmentos de reta. Assim, o termo “mediatriz de um triângulo” refere-se à mediatriz de um dos lados dessa figura geométrica. Portanto, o triângulo possui três mediatrizes. Veja a seguir:

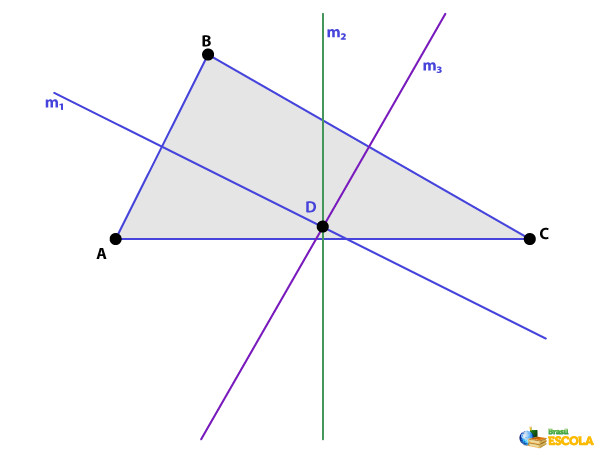
O ponto de encontro das mediatrizes de um triângulo é chamado de circuncentro, pois é o centro da circunferência circunscrita ao triângulo (ou seja, a circunferência que passa pelos três vértices do triângulo).

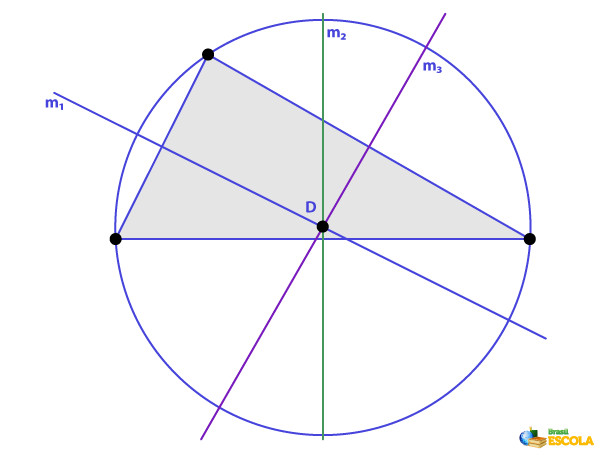
Importante: Como o circuncentro é um ponto comum às três mediatrizes, sua distância em relação a cada um dos vértices é a mesma. Em simbologia matemática, se D é o circuncentro do triângulo ABC, então \(AD=BD=CD\).

Diferenças entre mediatriz, mediana, bissetriz e altura de um triângulo

Mediatriz, mediana, bissetriz e altura de um triângulo são conceitos diferentes. Vejamos cada um de maneira individual e depois em conjunto.

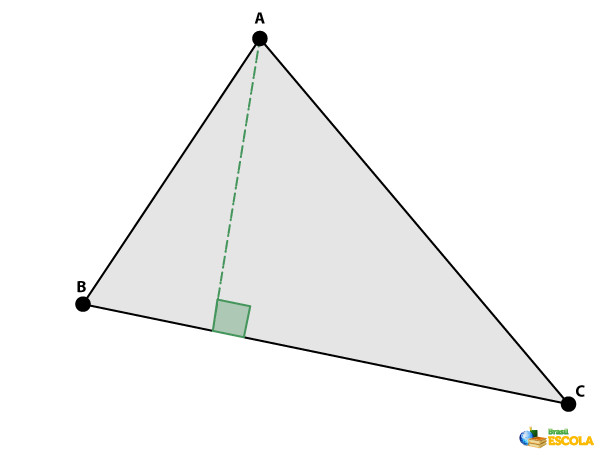
• Mediatriz de um triângulo: é a reta perpendicular a um dos lados que cruza seu ponto médio.

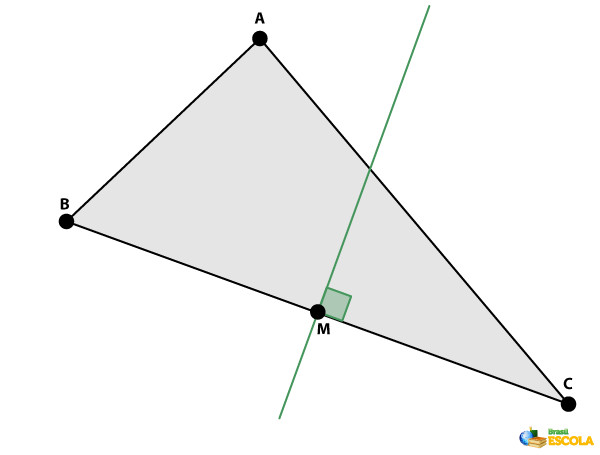
• Mediana de um triângulo: é o segmento com extremidades em um vértice do triângulo e no ponto médio do lado oposto ao vértice.

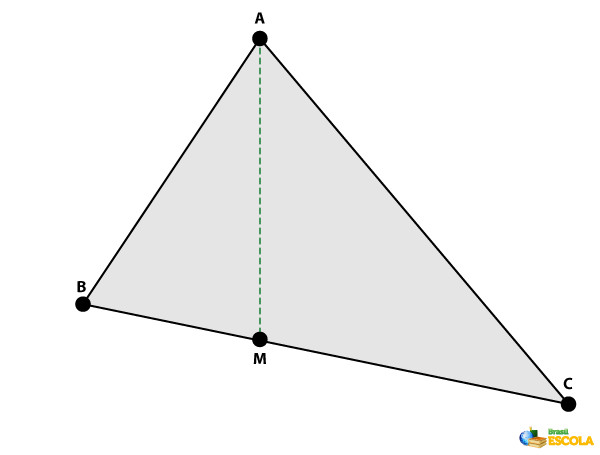
• Bissetriz de um triângulo: é o segmento que divide ao meio um dos ângulos internos do triângulo, com extremidades em um dos vértices e no lado oposto.

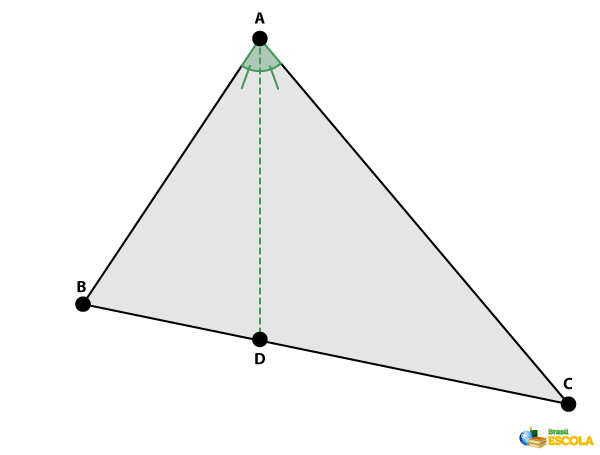
• Altura de um triângulo: é o segmento perpendicular a um dos lados com extremidade no ângulo oposto ao lado.

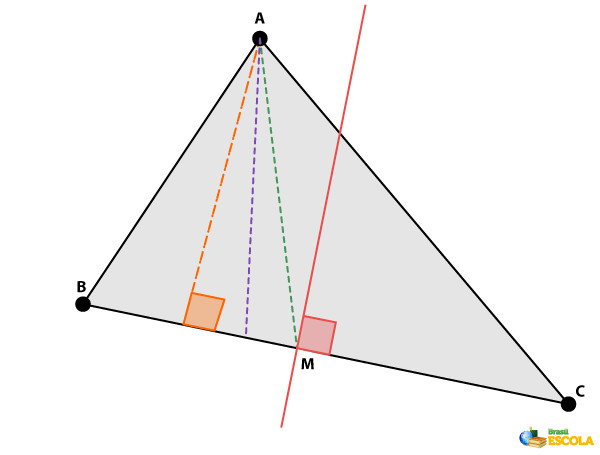
Na imagem a seguir, destacamos, em relação ao segmento BC do triângulo, a altura (linha pontilhada traço em laranja), a bissetriz (linha tracejada em roxo), a mediana (linha pontilhada em verde) e a mediatriz (linha contínua em vermelho).

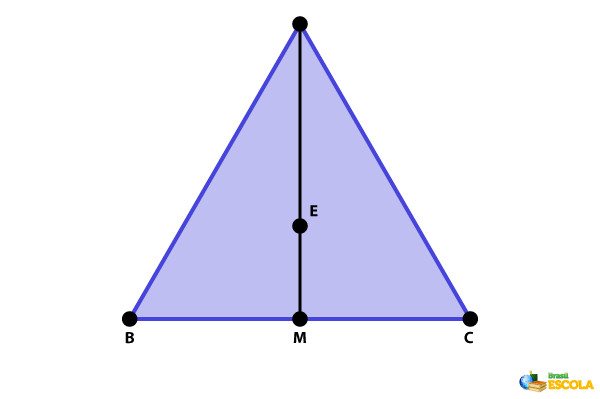
Importante: Em um triângulo equilátero, ou seja, que possui os três lados e três ângulos iguais, as mediatrizes, medianas, bissetrizes e alturas coincidem. Consequentemente, os pontos notáveis de um triângulo (circuncentro, baricentro, incentro e ortocentro) também coincidem. Na imagem a seguir, destacamos, em relação ao segmento BC, a mediatriz, mediana, bissetriz e altura em linha preta contínua. O ponto em evidência E é, portanto, o circuncentro, baricentro, incentro e ortocentro do triângulo ABC.

Veja também: Relações métricas no triângulo equilátero inscrito — quais são elas?

Exercícios resolvidos sobre mediatriz

Questão 1

Considere as afirmações a seguir.

I. A mediatriz de um triângulo é o segmento que começa em um vértice e cruza o ponto médio do lado oposto.

II. O ponto de encontro das mediatrizes de um triângulo é chamado de circuncentro. Esse ponto é o centro da circunferência circunscrita ao triângulo e equidista dos vértices.

III. A mediatriz de um segmento é a reta perpendicular que cruza o segmento no ponto médio.

Qual alternativa contém a(s) correta(s)?

A) I, apenas.

B) II, apenas.

C) III, apenas.

D) I e II.

E) II e III.

Resolução:

Alternativa E

A afirmação I é a única incorreta, pois descreve a mediana de um triângulo.

Questão 2

(Enem — adaptada) Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

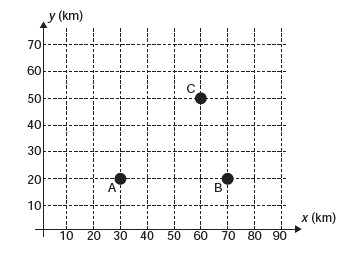
A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas

A) (65, 35).

B) (53, 30).

C) (45, 35).

D) (50, 20).

E) (50, 30).

Resolução:

Alternativa E

Perceba que a localização para a torre deve ser o circuncentro do triângulo formado pelos pontos A, B e C, pois é o local equidistante das três antenas.

As coordenadas para a torre T são \( (x_t,y_t )\). Como T pertence à mediatriz de AB (dada pela reta x = 50), a localização horizontal da torre deve ser \(x_t=50\).

Para determinar a coordenada horizontal \(y_t\) da torre, podemos utilizar duas vezes a expressão da distância entre dois pontos. Como a torre é equidistante, por exemplo, dos vértices A e C (AT = CT), temos que:

\(\sqrt{(30-50)^2+(20-y_t )^2}=\sqrt{(60-50)^2+(50-y_t )^2}\)

Simplificando, obtemos \(y_t=30\).

 

Por Maria Luiza Alves Rizzo
Professora de Matemática