Um quadrilátero pode ser circunscrito a uma circunferência se ocorrer tangência entre seus lados e a circunferência. Observe a figura a seguir:
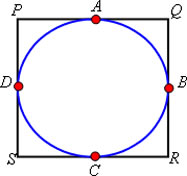
Nesses casos de quadriláteros circunscritos à circunferência, algumas propriedades são utilizadas no cálculo de medidas de segmentos.
Se somarmos os lados opostos dos quadriláteros circunscritos a uma circunferência, verificaremos que os resultados são iguais, isto é, possuem a mesma medida.
PQ + SR = QR + PS
Exemplo 1
Vamos determinar o valor de x na figura envolvendo um quadrilátero circunscrito a uma circunferência.
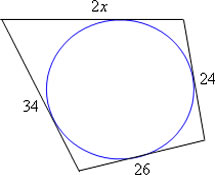
2x + 26 = 34 + 24
2x = 34 + 24 – 26
2x = 58 – 26
2x = 32
x = 32/2
x = 16
Exemplo 2
Determine a medida dos lados do quadrilátero circunscrito à circunferência de acordo com a figura a seguir.
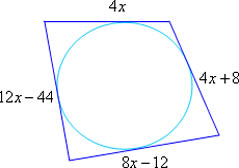
4x + 8x – 12 = 12x – 44 + 4x + 8
4x + 8x – 12x – 4x = – 44 + 8 + 12
– 4x = – 24
4x = 24
x = 24/4
x = 6
4x = 4 * 6 = 24
8x – 12 = 8 * 6 – 12 = 48 – 12 = 36
12x – 44 = 12 * 6 – 44 = 72 – 44 = 28
4x + 8 = 4 * 6 + 8 = 24 + 8 = 32
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola