Quadriláteros são polígonos com quatro lados. Diversos objetos, móveis e construções apresentam formas com quatro lados: janelas, pôsteres, capas de livros, folhas de caderno, telas de monitores e celulares, azulejos, pisos, etc.
Leia também: Classificação dos polígonos — regulares, irregulares, convexos e não convexos
Tópicos deste artigo
- 1 - Resumo sobre quadriláteros
- 2 - Videoaula sobre quadriláteros
- 3 - Elementos dos quadriláteros
- 4 - Tipos de quadriláteros
- 5 - Paralelogramos
- 6 - Trapézio
- 7 - Qual a diferença entre quadrilátero convexo e quadrilátero côncavo?
- 8 - Exercícios resolvidos sobre quadriláteros
Resumo sobre quadriláteros
-
Polígonos com quatro lados são quadriláteros.
-
Os três elementos básicos que constituem os quadriláteros são os lados, os vértices e os ângulos internos.
-
Paralelogramos são quadriláteros com 2 pares de lados paralelos.
-
O retângulo é um paralelogramo com 4 ângulos retos.
-
O quadrado é um paralelogramo com 4 ângulos retos e quatro lados congruentes.
-
O losango é um paralelogramo com 4 lados congruentes.
Anuncie aqui -
O trapézio é um quadrilátero com 1 par de lados paralelos, chamados de bases.
Videoaula sobre quadriláteros
Elementos dos quadriláteros
Os quadriláteros são constituídos por três elementos principais: lados, vértices e ângulos internos.
-
Lados são os segmentos de reta que delimitam o quadrilátero.
-
Vértices são os pontos em que dois lados se encontram.
-
Ângulos internos são as aberturas formadas por dois lados adjacentes.
Exemplo:
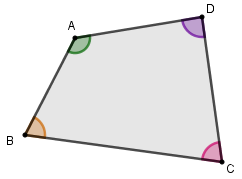
No quadrilátero ABCD, temos que
-
AB, BC, CD e AD são os lados;
-
A, B, C e D são os vértices;
-
\(\hat{A}\), \(\hat{B}\), \(\hat{C}\) e \(\hat{D}\) são os ângulos internos.
Observação: uma propriedade comum a todos os quadriláteros convexos é que a soma dos ângulos internos é 360°.
A diagonal é outro elemento importante dos quadriláteros e consiste no segmento cujas extremidades são vértices não consecutivos. No quadrilátero ABCD, as diagonais são os segmentos AC e BD.
Tipos de quadriláteros
Os quadriláteros são classificados de acordo com a quantidade de lados paralelos.
-
Os quadriláteros com 2 pares de lados paralelos são chamados de paralelogramos.
-
Os quadriláteros com 1 par de lados paralelos são chamados de trapézios.
Também há quadriláteros que não possuem nenhum par de lados paralelos, como o quadrilátero ABCD do tópico anterior.
Veja também: O que são retas paralelas?
Paralelogramos
Paralelogramos são quadriláteros com lados opostos paralelos. Consequentemente, os lados opostos e os ângulos opostos de um paralelogramo são congruentes.
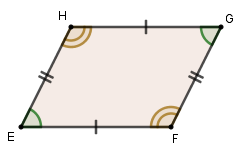
O retângulo, quadrado e losango são casos particulares de paralelogramos, como veremos adiante.
-
Retângulos
Um paralelogramo cujos ângulos são retos é chamado de retângulo.
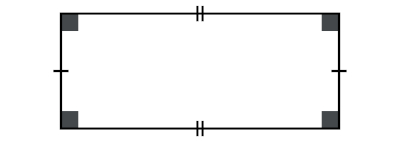
Assim, o retângulo apresenta as seguintes características:
-
lados opostos congruentes;
-
quatro ângulos de 90°;
-
diagonais congruentes que se interceptam nos respectivos pontos médios.
Anuncie aqui
Agora que sabemos o que é um retângulo, vamos descobrir como calcular a diagonal, o perímetro e a área desse quadrilátero.
-
-
Fórmulas do quadrilátero retângulo
-
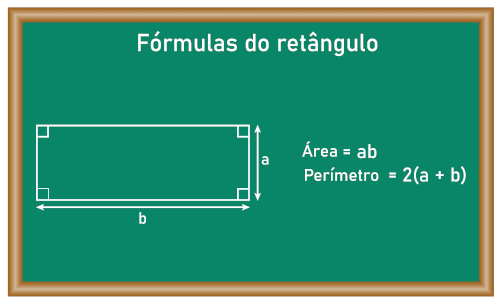
Considere um retângulo de largura a e comprimento b. Perceba que a medida da diagonal d pode ser obtida pela aplicação do teorema de Pitágoras:
\(d^2=a^2+b^2\)
\(d_{retângulo} =\sqrt{a^2+b^2}\)
Como o perímetro de um polígono é a soma de todos os lados, o perímetro P desse retângulo é dado por
\(P_{retângulo} =a+a+b+b\)
\(P_{retângulo} = 2a + 2b\)
\(P_{retângulo} =2⋅(a+b)\)
Já a área A de um retângulo é o produto entre o comprimento e a largura, ou seja
\(A_{retângulo} =a⋅b\)
-
Quadrado
Um paralelogramo cujos ângulos são retos e os lados são congruentes é chamado de quadrado.
Portanto, o quadrado possui as seguintes características:
-
quatro lados congruentes;
-
quatro ângulos de 90°;
-
diagonais congruentes que se interceptam nos respectivos pontos médios.
Note que o quadrado também pode ser classificado como um retângulo, pois é um paralelogramo com quatro ângulos retos. No entanto, o contrário não é verdade, ou seja, o retângulo não é um quadrado, pois não possui quatro lados congruentes.
Agora que sabemos exatamente o que é um quadrado, vejamos como calcular a medida da diagonal, do perímetro e da área desse polígono.
-
-
Fórmulas do quadrilátero quadrado
-
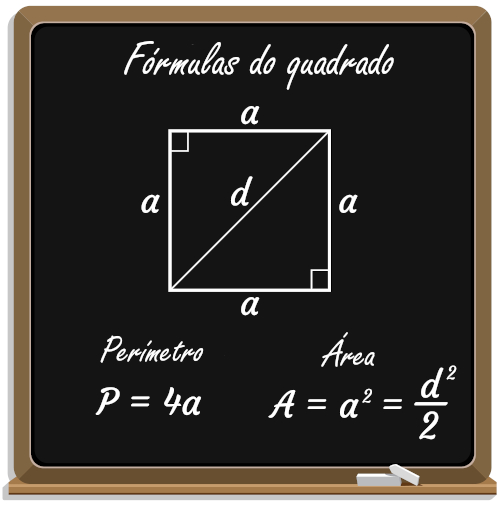
Considere um quadrado de lado a. Note que a medida da diagonal d pode ser determinada pelo teorema de Pitágoras:
\(d^2=a^2+a^2\)
\(d^2=2a^2\)
\(d_{quadrado} =a\sqrt2\)
Já o perímetro é a soma dos quatro lados de medida a, ou seja
\(P_{quadrado} =a+a+a+a\)
\(P_{quadrado} =4a\)
Por fim, a área é o produto entre dois lados adjacentes, ou seja
\(A_{quadrado} =a⋅a\)
\(A_{quadrado} =a^2\)
-
Losango
Um paralelogramo cujos lados são congruentes é chamado de losango.
Logo, o losango apresenta as seguintes características:
-
quatro lados congruentes;
Anuncie aqui -
ângulos opostos congruentes;
-
diagonais perpendiculares que se interceptam nos respectivos pontos médios.
Perceba que o quadrado também pode ser classificado como um losango, pois é um paralelogramo com quatro lados congruentes. No entanto, o contrário não é verdade, ou seja, o losango não é um quadrado, pois não possui quatro ângulos retos.
Agora que conhecemos o losango, vamos descobrir como calcular a medida da área e do perímetro desse polígono.
-
-
Fórmulas do quadrilátero losango
-
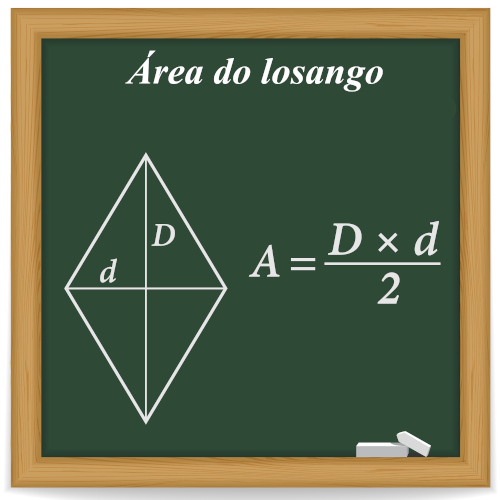
Considere um losango de lado l, diagonal menor d e diagonal maior D. Como o perímetro de um polígono é a soma das medidas dos lados, o perímetro P do losango é dado por
\(P_{losango} =l+l+l+l\)
\(P_{losango} =4⋅l\)
Já a área é a metade do produto entre a diagonal maior D e a diagonal menor d:
\(A_{losango} =\frac{D⋅d}2\)
Trapézio
Como estudamos no início do texto, um trapézio é um quadrilátero que possui um par de lados paralelos. Esses lados são chamados de bases, e os lados não paralelos são chamados de laterais do trapézio.
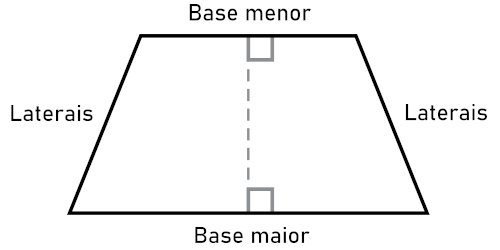
-
Fórmulas do quadrilátero trapézio
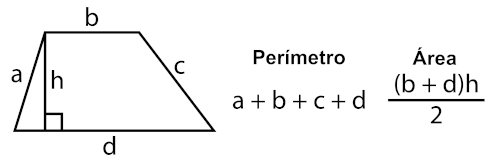
Considere um trapézio em que a base menor mede b, a base maior d e as laterais a e c. Assim, o perímetro P do trapézio é dado por
\(P_{trapézio} =a+b+c+d\)
Já a área é a metade do produto entre a altura do trapézio (que é a distância entre as bases) e a soma das bases:
\(A_{trapézio} =\frac{base\ menor\ +\ base\ maior ⋅h}2\)
\(A_{trapézio} =\frac{(b+d)⋅h}2\)
Saiba mais: Como calcular a área de figuras planas
Qual a diferença entre quadrilátero convexo e quadrilátero côncavo?
Um polígono é chamado de convexo se, dados dois pontos pertencentes ao polígono, o segmento com extremidades nesses pontos está contido no polígono. Caso contrário, o polígono é não convexo (ou côncavo). O mesmo se aplica no caso dos quadriláteros, conforme o exemplo abaixo.
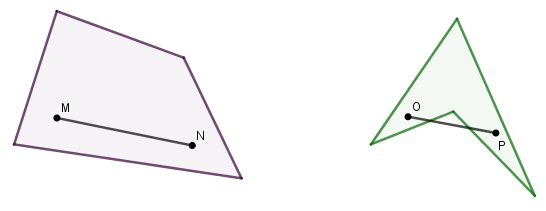
Note que os pontos M e N pertencem ao primeiro quadrilátero, e o segmento MN está contido nesse quadrilátero. Isso se observaria para quaisquer dois pontos pertencentes ao polígono. Assim, é um quadrilátero convexo.
Agora observe que os pontos P e O pertencem ao segundo quadrilátero, mas o segmento PO não está contido nesse quadrilátero. Sendo assim, esse é um quadrilátero não convexo (côncavo).
Exercícios resolvidos sobre quadriláteros
Questão 1
Se o perímetro de um quadrado mede 100 cm, a área desse polígono é igual a
a) 1000 cm²
b) 625 cm²
c) 500 cm²
d) 400 cm²
e) 250 cm²
Resolução
Considere a o lado do quadrado. Assim,
\(P_{quadrado} =4a\)
\(100 = 4a\)
\(a = 25\ cm\)
Portanto,
\(A_{quadrado} =a^2\)
\(A_{quadrado} =25^2\)
\(A_{quadrado} =625\ cm^2\)
Alternativa B.
Questão 2
Considere um retângulo cuja diagonal mede 10 cm e a largura mede 6 cm. Nessas condições, a medida do comprimento, em centímetros, é igual a
a) 8
b) 10
c) 12
d) 14
e) 16
Resolução
Sendo b o comprimento do retângulo,
\(d_{retângulo} =\sqrt{a^2+b^2}\)
\(10=\sqrt{6^2+b^2}\)
\(10^2=6^2+b^2\)
\(100=36+b^2\)
\(b^2=64\)
\(b= 8\ cm\)
Alternativa A.
Fontes
LIMA, E. L. Geometria Analítica e Álgebra Linear. Rio de Janeiro: IMPA, 2014.
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.
Por Maria Luiza Alves Rizzo
Professora de Matemática


