Paralelogramos

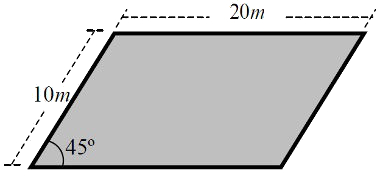
Os paralelogramos são polígonos da geometria plana bastante explorados por serem figuras geométricas comuns no nosso dia a dia. Definimos como paralelogramo um polígono que possui lados opostos paralelos, característica essa que resulta em propriedades exclusivas.

Os casos particulares de paralelogramos são os quadrados, retângulos e losangos. Para cada um desses polígonos, há fórmulas específicas para o cálculo de área e perímetro.

Leia também: Círculo e circunferência – formas geométricas com muitas particularidades

Tópicos deste artigo

• 1 - Elementos de um paralelogramo
• 2 - Propriedades de um paralelogramo
• 3 - Área de um paralelogramo
• 4 - Perímetro de um paralelogramo
• 5 - Casos especiais de paralelogramos
  • Quadrado
  • Retângulo
• 6 - Relação entre os paralelogramos
• 7 - Exercícios resolvidos sobre paralelogramo

Elementos de um paralelogramo

Para ser um paralelogramo, o polígono deve possuir os lados opostos paralelos. Como características específicas, temos que:

• Todo paralelogramo é composto por quatro lados, e os lados opostos são paralelos.

• Todo paralelogramo possui quatro ângulos internos, e a soma desses ângulos é sempre igual a 360º.

• Todo paralelogramo possui duas diagonais.

Vale lembrar que os paralelogramos são casos particulares de quadriláteros, então existem características que são herdadas dessas figuras geométricas, como a existência de duas diagonais, quatro lados e quatro ângulos, bem como a soma dos ângulos internos e dos ângulos externos ser sempre igual a 360º.

Propriedades de um paralelogramo

• 1ª propriedade: Os lados opostos de um paralelogramo são congruentes, isto é, possuem a mesma medida.

• 2ª propriedade: Os ângulos opostos de um paralelogramo são congruentes, e dois ângulos consecutivos são sempre suplementares (a soma é igual a 180º).

Sabendo que AB e CD são paralelos, então os lados BC e AD são transversais de AB e CD; consequentemente, os ângulos formados (w e x) são suplementares, pois são ângulos colaterais internos. Além disso, é possível demonstrar que os ângulos x e z são congruentes.

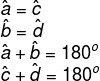
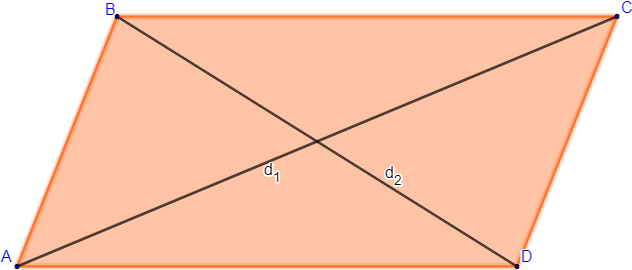
• 3ª propriedade: As diagonais de um paralelogramo cortam-se ao meio.

Quando traçamos as duas diagonais de um paralelogramo, o ponto de encontro delas divide cada uma delas em seus pontos médios.

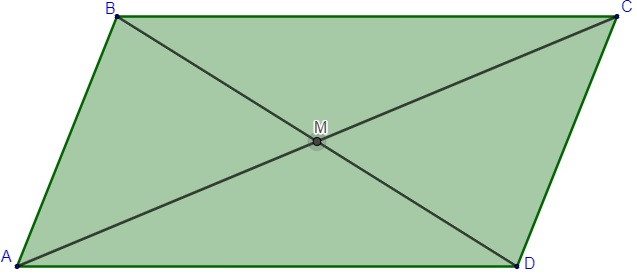
AM = CM

BM= DM

Veja também: Ponto, reta, plano e espaço: conceitos básicos da geometria

Área de um paralelogramo

A área de um paralelogramo, de modo geral, é calculada pelo produto da base pela altura. Há casos particulares (retângulos, losangos e quadrados) que possuem fórmulas específicas – serão apresentadas no decorrer deste texto –, mas que surgem a partir da forma geral.

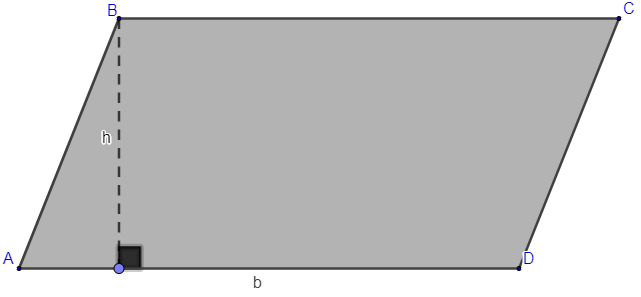
A = b.h

b: base

h: altura

Perímetro de um paralelogramo

O perímetro é dado pela soma de todos os lados. Como um paralelogramo possui, de forma geral, dois lados iguais, o seu perímetro pode ser determinado por:

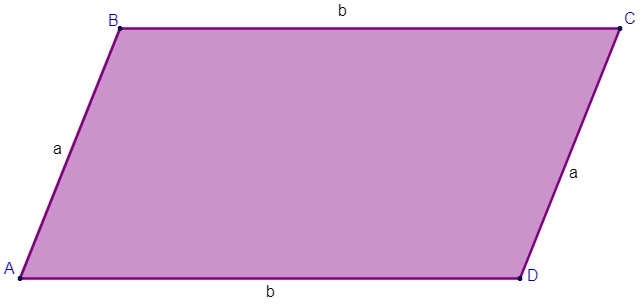
P = 2 (a + b)

Casos especiais de paralelogramos

Como sabemos, por definição, para que seja um paralelogramo, o polígono precisa ter lados paralelos. Existem três quadriláteros que são tratados como casos particulares do paralelogramo: o retângulo, o losango e o quadrado.

• Quadrado

Chamamos de quadrado um polígono de quatro lados que possui os quatro lados e os quatro ângulos congruentes – cada ângulo possui exatamente 90º. Como o quadrado é um paralelogramo, todas as propriedades são válidas para o quadrado.

A área de um quadrado e o seu perímetro são calculados de forma parecida com o que é feito com um paralelogramo, mas como todos os lados do quadrado são iguais, podemos representar a área e o perímetro do quadrado desta forma:

A= l²

P = 4.l

• Retângulo

O retângulo é um paralelogramo que possui todos os ângulos congruentes. Ele recebe esse nome porque todos os seus ângulos são retos, ou seja, os quatro ângulos medem 90º. A área do retângulo é idêntica à área do paralelogramo, mas podemos tratar o lado na vertical como a altura, afinal, ele é perpendicular à base.

A=a .b

P= 2 (a + b)

• Losango

O losango é um paralelogramo que possui todos os seus lados congruentes. Note que não há nenhuma restrição para os ângulos, podendo eles ser diferentes ou não. De maneira distinta dos exemplos anteriores, o cálculo da área de um losango é feito com base nas suas diagonais. Também existe uma relação muito importante entre as diagonais do losango e o seu lado.

 

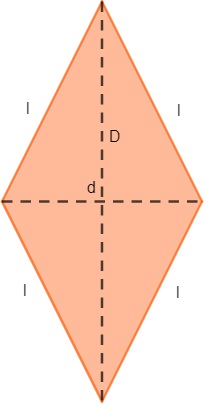
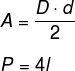
D: diagonal maior

d: diagonal menor

l: lado

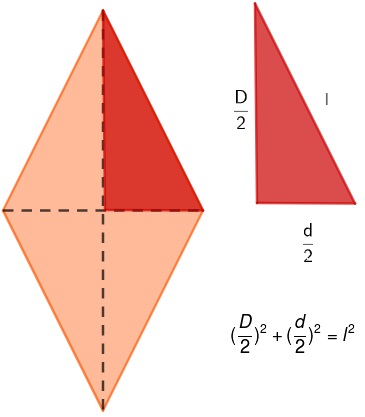
Dado um losango qualquer, sabemos que as diagonais se cruzam no ponto médio, formando quatro triângulos retângulos. Analisando um desses triângulos, é possível perceber uma relação pitagórica entre o lado e a metade de cada uma das diagonais.

Acesse também: Comprimento da circunferência e área do círculo

Relação entre os paralelogramos

É importante entender bem a definição de paralelogramo, para não ter complicação durante a classificação. É sempre bom lembrar que todo paralelogramo é um quadrilátero, mas nem todo quadrilátero é um paralelogramo.

Podemos afirmar também que todo retângulo, todo quadrado e todo losango são paralelogramos. Além disso, comparando os casos especiais de paralelogramos, podemos perceber outra relação, pois o quadrado possui ângulos congruentes, que é a definição de retângulo, e também lados congruentes, que é a definição de losango. Como consequência, podemos afirmar que todo quadrado é um retângulo e também um losango.

Exercícios resolvidos sobre paralelogramo

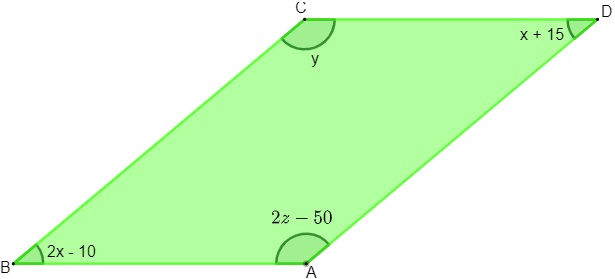
Questão 1 - Sabendo que a figura abaixo é um paralelogramo, qual será o valor de x, y e z respectivamente?

a) 40,140 e 180

b) 30, 100 e 100

c) 25, 140 e 95

d) 30, 90 e 145

e) 45, 55 e 220

Resolução

1º passo: Utilizando a propriedade do paralelogramo, sabemos que ângulos opostos são iguais. Ao analisar a imagem, é mais conveniente utilizar essa propriedade nos ângulos do vértice B e D, pois possuem mesma incógnita.

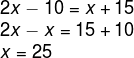
2º passo: Sabendo que ângulos consecutivos são suplementares e que x = 25, é possível encontrar o valor de y.

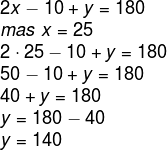
3º passo: Como os ângulos dos vértices C e A são opostos, eles são congruentes, logo podemos encontrar o valor de z.

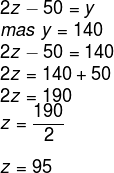
Alternativa C.

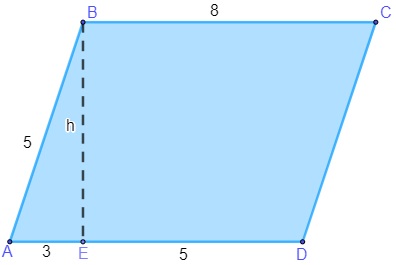
Questão 2 - Calcule a área do paralelogramo (lados medidos em centímetros) a seguir.

a) 16 cm²

b) 32 cm²

c) 8 cm²

d) 64 cm²

e) 40 cm²

Resolução

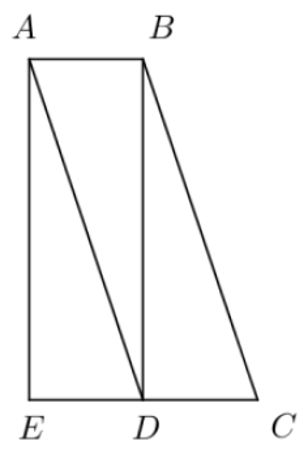
Para encontrar a área do paralelogramo, primeiro é necessário encontrar o valor de h. Note que o triângulo AEB é retângulo de hipotenusa igual a 5, logo podemos aplicar o teorema de Pitágoras para encontrar o valor de h.

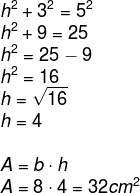
Alternativa B.