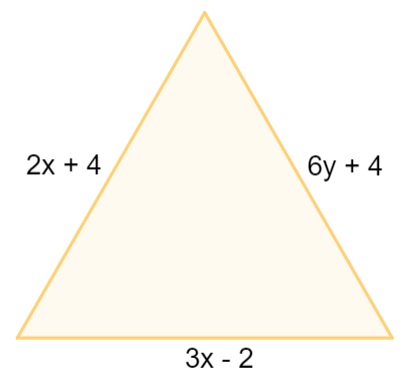
O triângulo equilátero é um tipo especial de triângulo. Por essa razão, todas as propriedades que valem para os triângulos são válidas para ele, mas esse tipo também possui propriedades específicas.
Quando um polígono possui somente três lados, ele é conhecido como triângulo. Essa forma geométrica pode ser classificada quando se comparam seus lados. Assim, um triângulo pode ser escaleno, quando todos os lados são diferentes; isósceles, quando dois lados são congruentes; e equilátero, quando os três lados são congruentes.
O triângulo equilátero possui características específicas em razão das medidas iguais. Há, inclusive, fórmulas para cálculo de área e perímetro que são eficientes somente para triângulos equiláteros
Leia também: Pirâmides – figuras geométricas cujas faces laterais são formadas por triângulos
Tópicos deste artigo
- 1 - Propriedades do triângulo equilátero
- 2 - Perímetro do triângulo equilátero
- 3 - Área do triângulo equilátero
- 4 - Exercícios resolvidos
Propriedades do triângulo equilátero
Um triângulo é conhecido como equilátero quando ele possui a medida dos três lados congruentes, assim, consequentemente, os seus ângulos internos também são congruentes. Como a soma dos ângulos internos de um triângulo é sempre igual a 180º e os ângulos são iguais, ao dividirmos 180º por 3, chegaremos a ângulos de 60º. Os ângulos internos do triângulo equilátero, portanto, sempre medem 60°.
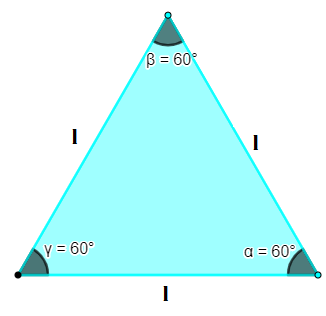
Em razão dessas características, o triângulo equilátero possui propriedades específicas. Se traçarmos a altura do triângulo equilátero, ela também será bissetriz (segmento de reta que divide o ângulo em duas partes congruentes) e mediana (segmento de reta que liga o vértice ao ponto médio do lado oposto).
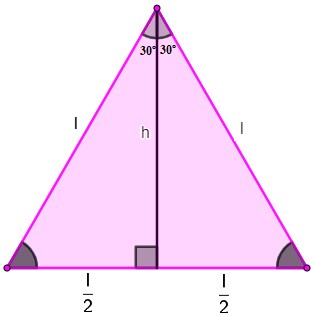
Ao dividirmos o triângulo como feito na imagem anterior, a altura do triângulo pode ser escrita em função do lado, o que pode ser demonstrado tanto por trigonometria quanto pelo teorema de Pitágoras.
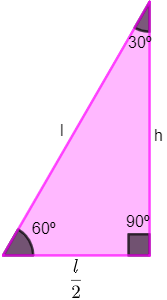
A fórmula para calcular a altura de um triângulo equilátero é:
![]()
Leia também: Mediana, bissetriz e altura de um triângulo
→ 1ª demonstração:
No teorema de Pitágoras, é demonstrado que existe uma relação entre os lados de um triângulo retângulo. A soma do quadrado dos catetos é igual à hipotenusa ao quadrado. A hipotenusa é o maior lado oposto ao ângulo de 90º (no nosso caso, o lado que mede l), e os catetos são os outros dois lados. Então, temos que:
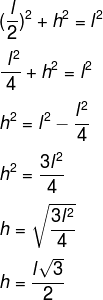
→ 2ª demonstração:
Vale lembrar dois dados importantes da trigonometria. Um deles é o seno de um ângulo e o outro é o valor do seno de 60º.
O seno de um ângulo qualquer é dado pela relação entre o cateto oposto e a hipotenusa do triângulo retângulo:
![]()
Vale lembrar também os ângulos notáveis, que são os ângulos de 30º, 45º e 60º. Neste caso usaremos o ângulo de 60º, então é importante pontuar que:
![]()
Isso torna possível demonstrar que a altura só depende de h. Veja:
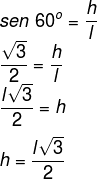
Independentemente do tipo de demonstração, é possível perceber que a altura (h) depende somente do valor do lado para ser calculada.
Perímetro do triângulo equilátero
Perímetro é a soma de todos os lados de um polígono. Como o triângulo equilátero é um polígono regular, ou seja, possui todos os três lados congruentes, o cálculo do seu perímetro é muito simples, depende somente da medida do lado l de um triângulo equilátero. Como ele possui os três lados com a mesma medida, temos que:
P = 3l
Exemplo 1:
Calcule o perímetro do triângulo equilátero cujo lado mede 9 cm.
Resolução:
P = 3l
P = 3.9 = 27 cm
Exemplo 2:
Para cercar um terreno com 5 voltas de arame, foram necessários 450 metros de arame. Sabendo que o terreno tem o formato de um triângulo equilátero, qual é a medida de cada um dos seus lados?
Resolução:
Temos como dado 5 vezes o perímetro e queremos descobrir o valor dos lados.
Sendo assim, temos que:
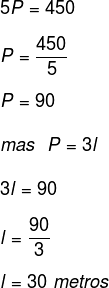
Acesse também: Área do prisma – cálculo feito a partir da planificação de sólidos geométricos
Área do triângulo equilátero
Entendemos que área de um triângulo qualquer é dada pela multiplicação da base pela altura dividida por dois, mas o triângulo equilátero possui uma fórmula especial para ele, que é a seguinte:
![]()
→ Demonstração da fórmula:
A área de um triângulo qualquer é dada por:
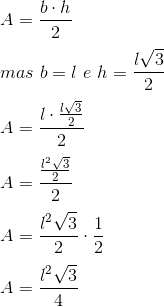

Exercícios resolvidos
Questão 1 - A área e a altura de um triângulo equilátero que possui um perímetro de 15 cm são, respectivamente (sugestão: use √3 = 1,7)?
a) 15 e 225
b) 5 e 11,3
c)10,5 e 21
d) 4,25 e 10,625
e) 8,5 e 22,5
Resolução
- 1º passo: encontrar o valor do lado l.
Se o perímetro é 15 cm, significa que 3l é igual a 15, logo o lado do triângulo é 5 cm.
- 2º passo: calcular altura.
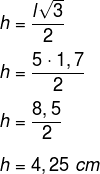
- 3º passo: calcular a área.
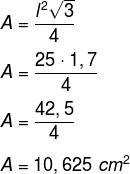
Letra d.
Questão 2 - Um triângulo equilátero possui lados medindo y, 2x + 3 e 4x – 2, logo os valores de x e y são, respectivamente:
a) 5 e 16
b) 16 e 5
c) 4 e 2
d)8 e 2,5
e) 2,5 e 8
Resolução:
Um triângulo equilátero possui lados congruentes, então:
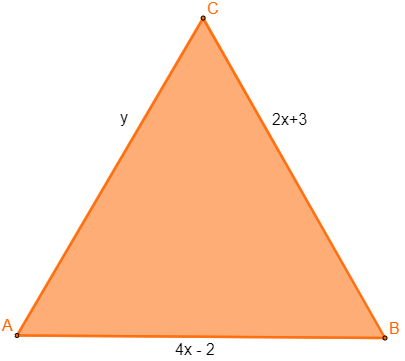
Primeiro, vamos igualar os lados que possuem mesma incógnita:
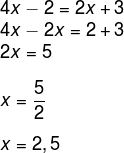
Sabendo o valor de x, escolhemos qualquer um dos lados que possui essa incógnita e igualamos a y.
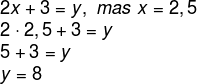
Letra E.
Por Raul Rodrigues de Oliveira
Professor de Matemática