Porcentagem envolve diversas situações com que nos deparamos frequentemente em nosso cotidiano, por exemplo em indicadores econômicos, resultados de pesquisas ou promoções. Entendemos porcentagem como sendo a razão entre um número qualquer e 100, sendo representada pelo símbolo %. Utilizamos a ideia de porcentagem para representar partes de algo inteiro.
Leia também: Cálculo da composição de porcentagem
Tópicos deste artigo
- 1 - Representações da porcentagem
- 2 - Como calcular a porcentagem?
- 3 - Exercícios resolvidos
- 4 - Perguntas frequentes
Representações da porcentagem
Sabemos que a porcentagem é uma razão, logo, pode ser representada por uma fração, que, por sua vez, pode ser escrita na forma decimal. De modo geral, se temos um número acompanhado pelo símbolo %, basta dividi-lo por 100, ou seja:
![]()
Veja os exemplos seguintes que mostram as diferentes representações de porcentagens. Lembre-se, para “transformar” a porcentagem em fração, basta dividir o número que acompanha o símbolo % por 100 e simplificar a fração; para “transformar” a fração em forma decimal, basta realizar a divisão.
-
Exemplo
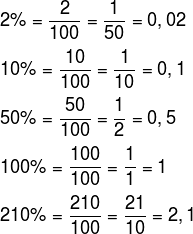
Perceba que quando escrevemos a porcentagem 100% é o mesmo que considerar um inteiro, ou seja, quando consideramos 100% de algo, estamos levando em conta o total daquilo. No caso de 210%, estamos considerando mais que um inteiro, isto é, consideramos 2,1 vezes o total.
Para fazer o caminho de volta, ou seja, dado uma fração ou um número decimal para ser escrito na forma percentual, basta multiplicar o número em questão por 100. Veja:
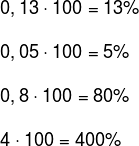
Leia também: Cálculo de porcentagem com regra de três
Como calcular a porcentagem?
Para realizar o cálculo da porcentagem de um valor, basta multiplicar esse valor pela porcentagem em sua forma decimal ou fracionária.
-
Exemplo
- Calcule 50% de 600.
Sabemos que 50% = 0,5, assim, basta fazer a substituição e multiplicar os valores. Veja:
0,5 . 600
300
Podendo também substituir os 50% na forma fracionária, ficando:
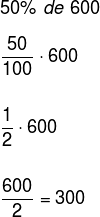
Logo, 50% de 600 = 300. Veja que 50% representam a metade do total que é 600.
Exercícios resolvidos
Questão 1 - (Enem) Uma pessoa investiu certa quantia em dinheiro na bolsa de valores. No primeiro mês, ela perdeu 30% do que investiu e, no segundo mês, teve um lucro de 40% sobre o saldo que havia ficado após o prejuízo. Após esses dois meses, essa pessoa teve com esse investimento, em relação ao capital inicial aplicado,
- um prejuízo de 2%.
- um lucro de 2%.
- um prejuízo de 4%.
- um lucro de 4%.
- o mesmo valor de capital aplicado.
Solução
Seja x o valor que foi investido na bolsa de valores, como no primeiro mês a pessoa teve um prejuízo de 30% desse valor, então temos que calcular essa porcentagem em relação ao valor investido e, em seguida, subtrair do valor investido. Veja:
30% de x
0,3 . x
0,3x a prejuízo
Então o que sobrou na conta dessa pessoa foi:
x – 0,3x
0,7x
Como, em seguida, a pessoa teve um lucro de 40% sobre o valor que tinha sobrado, temos que calcular essa porcentagem em cima desse valor e, em seguida, somar o resultado disso ao valor sobrado, tendo:
40% de 0,7x
0,4 · 0,7x
0,28x a lucro
Logo, temos que o valor que restou é:
0,7x + 0,28x
0,98x
Em relação ao que foi investido inicialmente, temos que a diferença é:
x – 0,98x
0,02x
Assim, ele teve um prejuízo de 2% em relação ao valor investido inicialmente.
R: alternativa a
Questão 2 - Calcule o valor de (30%)2.
Solução
![]()
Perguntas frequentes
Como fazer o cálculo de porcentagem?
- Para realizar o cálculo da porcentagem de um valor, basta multiplicar esse valor pela porcentagem em sua forma decimal ou fracionária.