Regra de três simples

A regra de três é um método que utilizamos para encontrar valores desconhecidos quando estamos trabalhando com grandezas direta ou inversamente proporcionais. Esse método de resolução tem bastante aplicação não só na matemática, como na física, química e em situações constantes do dia a dia. O trabalho com grandezas é fundamental em várias áreas do conhecimento, e, na regra de três, é importante conseguir-se identificar grandezas que se relacionam de forma direta e grandezas que se relacionam de forma inversa.

Leia também: Três erros mais cometidos na regra de três

Tópicos deste artigo

• 1 - Grandezas direta e inversamente proporcionais
• 2 - Como resolver uma regra de três simples?
  • Grandezas diretamente proporcionais
  • Grandezas inversamente proporcionais 
• 3 - Regra de três simples e composta
• 4 - Exercícios resolvidos sobre regra de três simples

Grandezas direta e inversamente proporcionais

A comparação entre duas grandezas é bastante comum e necessária no cotidiano, e quando comparamos e verificamos sua proporção, podemos separá-las em dois casos importantes: grandezas diretamente proporcionais ou grandezas inversamente proporcionais.

• Diretamente proporcionais: à medida que uma dessas grandezas aumenta, a outra também aumenta e na mesma proporção. Existem várias situações no nosso cotidiano que envolvem grandezas diretamente proporcionais, um exemplo seria a relação preço e peso na compra de uma determinada verdura, quanto menor a quantidade, menor o preço, e quanto maior a quantidade, maior o preço.

• Inversamente proporcionais: à medida que uma dessas grandezas aumenta, a outra grandeza diminui na mesma proporção. Um exemplo dessa situação no cotidiano é a relação entre velocidade e tempo. Quanto maior a velocidade para percorrer-se determinado percurso, menor será o tempo.

Como resolver uma regra de três simples?

Para resolver-se situações utilizando a regra de três, é fundamental que exista a proporcionalidade, além disso, é de grande importância a identificação da relação entre as grandezas.

Os problemas que envolvem regra de três simples podem ser separados em dois casos, quando as grandezas são diretamente proporcionais ou inversamente proporcionais. Ao deparar-se com qualquer questão que possa ser resolvida com regra de três, seguimos os seguintes passos:

1º passo – Identificar as grandezas e construção da tabela.

2º passo – Analisar se as grandezas são diretamente ou inversamente proporcionais.

3º passo – Aplicar o método de resolução correto para cada um dos casos, e, por fim, resolver a equação.

• Grandezas diretamente proporcionais

Exemplo:

Para revitalização de um parque, a comunidade organizou-se em um projeto conhecido como Revitalizar. Para que o projeto fosse eficiente, foram arrecadadas várias mudas frutíferas. Um planejamento para o plantio foi feito, e nele 3 pessoas trabalhavam no plantio e plantavam, por dia, 5 m². Devido à necessidade de um plantio mais eficiente, mais 4 pessoas, todas com o mesmo desempenho, comprometeram-se a participar da causa, sendo assim, qual será a quantidade de m² reflorestada por dia?

As grandezas são pessoas e área reflorestada.

Inicialmente havia 3 pessoas, e agora há 7.

Inicialmente havia 5 m² de plantio por dia, porém não sabemos a quantidade de m² que será cultivada pelas 7 pessoas, então representamos esse valor por x.

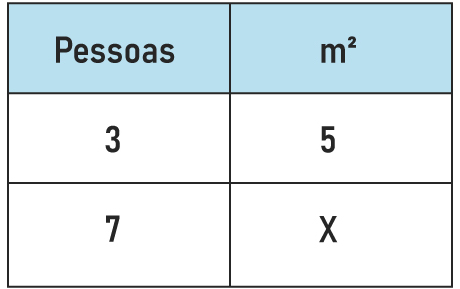
Agora é fundamental a comparação entre as duas grandezas. À medida que eu aumento o número de pessoas, a quantidade de m² reflorestada por dia aumenta na mesma proporção, logo, essas grandezas são diretamente proporcionais.

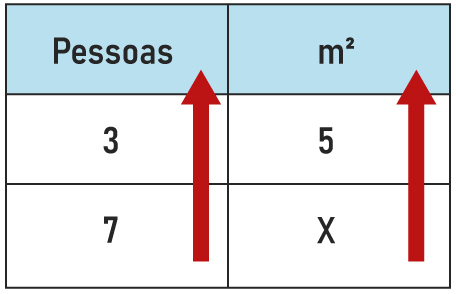
Quando as grandezas são diretamente proporcionais, basta multiplicar os valores da tabela de forma cruzada, gerando a equação:

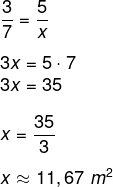
Veja também: O que é proporção?

• Grandezas inversamente proporcionais 

Exemplo: 

Para a confecção das provas de um concurso, uma gráfica dispunha de 15 impressoras, que demorariam 18 horas para imprimir todas as provas. No preparo para o início do trabalho, foi diagnosticado que só havia 10 impressoras funcionando. Qual é o tempo, em horas, que será gasto para a confecção de todas as provas do concurso?

As grandezas são quantidades de impressoras e tempo.

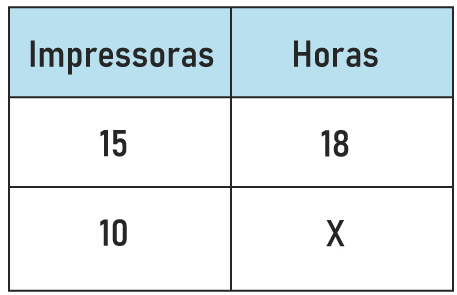
Analisando-se as duas grandezas, é notório que se a quantidade de impressoras for diminuída, consequentemente, o tempo para fazer as impressões será aumentado, logo, essas grandezas são inversamente proporcionais.

Quando as grandezas são inversamente proporcionais, é necessário inverter-se a fração (trocar numerador e denominador) de uma das frações, para, posteriormente, multiplicar-se cruzado.

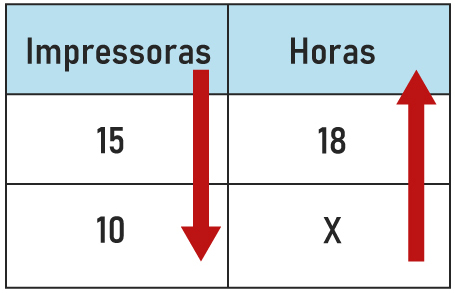
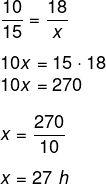
Dica: Em resumo, quando as grandezas são inversamente proporcionais, sempre invertemos uma das frações e multiplicamos cruzado — detalhe esquecido durante muitas resoluções de problemas e que faz muitos estudantes errarem ao esquecerem-se de analisar qual tipo de proporcionalidade (direta ou inversa) o problema está trabalhando.

Regra de três simples e composta

Existem duas formas de aplicar-se a regra de três, a regra de três simples, quando o problema envolve duas grandezas, e a regra de três composta, quando o problema envolve mais grandezas. Então a regra de três composta nada mais é que uma extensão da regra de três simples quando há um número maior de grandezas, e, para compreendê-la, a regra de três simples é fundamental.

Acesse também: Cálculo de porcentagem com regra de três

Exercícios resolvidos sobre regra de três simples

Questão 1 – Em uma granja com 800 frangos, 984 kg duram exatamente 10 dias. Caso a granja tivesse 200 frangos a mais, essa ração duraria:

A) 9 dias

B) 8 dias

C) 7 dias

D) 6 dias

E) 12 dias

Resolução

Alternativa B

Primeiro vamos identificar as grandezas, são elas: tempo e quantidade de frangos. Agora é possível montar a tabela e analisar se elas são diretas ou inversamente proporcionais. Sabemos que quanto maior a quantidade de frangos, menos tempo a ração vai durar, logo, as grandezas são inversamente proporcionais.

A informação da quantidade de ração torna-se irrelevante para responder o problema.

Sabemos que 800 + 200 = 1000, e queremos descobrir por quanto tempo a ração duraria se tivessem 1000 frangos.

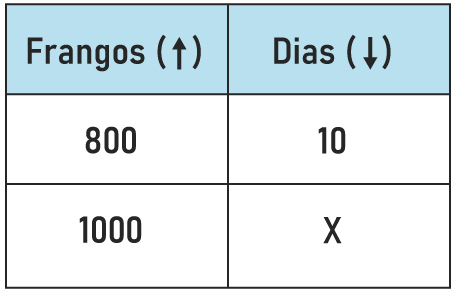
Como são inversamente proporcionais, multiplicaremos reto:

1000x = 800 · 10

1000x = 8000

x = 8000 : 1000

x = 8 dias

Questão 2 – Para analisar os processos de multa de trânsito, a prefeitura dispôs de 18 funcionários, que conseguiam realizar o trabalho diariamente analisando 135 processos. Em um dia, infelizmente, 4 funcionários não compareceram. Supondo-se que todos os funcionários atendem a mesma demanda de processos, nesse dia, a quantidade de processos analisados será de:

A) 135

B) 120

C) 110

D) 105

E) 100

Resolução

Alternativa D

Analisando-se a situação, as grandezas são: quantidade de funcionários e quantidade de processos. Sabemos que quanto mais funcionários tiver, mais processos serão analisados, logo, as grandezas são diretamente proporcionais. 18 – 4 = 14 funcionários. Montando a tabela, temos que:

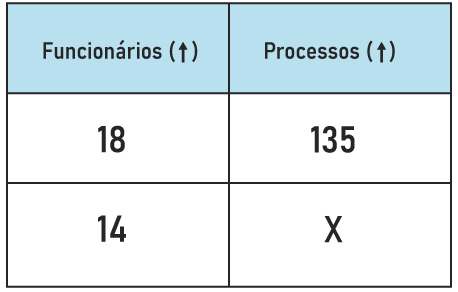
Como as grandezas são diretamente proporcionais, multiplicaremos cruzado:

18x = 135 · 14

18x = 1890

x = 1890 : 18

x = 105