Segmentos de reta são partes da reta que possuem ponto inicial e ponto final. Dessa forma, é possível medir o comprimento de um segmento de reta, diferentemente da reta, que não possui um ponto inicial ou um ponto final. Ela é infinita.
Para afirmar que segmentos de reta são proporcionais, é preciso saber primeiro o que é proporcionalidade. Para compreender bem, por sua vez, a proporcionalidade, é necessário entender as razões.
Razão é o resultado da divisão entre dois números reais. Assim, se “a” e b” são números reais, e a divisão entre eles tem como resultado “c”, então dizemos que a razão entre “a” e “b” é igual a “c” e escrevemos:
a = c
b
Muito comum é encontrar duas razões que possuem o mesmo resultado. Razões que resultam de um processo de simplificação de frações, por exemplo, têm resultados iguais. Observe:
2 = 6 = 8 = 2
1 3 4
Essas razões que possuem o mesmo resultado são chamadas de proporções e dizemos que os números que as geraram são proporcionais. Com base nesse raciocínio, quatro números, por exemplo, são proporcionais quando as razões formadas por eles, ordenadamente, são iguais.
Em outras palavras, dados os números A, B, C e D, caso a seguinte igualdade seja válida, dizemos que esses números são proporcionais.
A = C
B D
Segmentos proporcionais:
Uma vez que os segmentos de reta são “pedaços” da reta que podem ser medidos, a definição de proporcionalidade acima fica válida e, de certa forma, até óbvia. Basta conhecer as medidas de quatro segmentos de reta e verificar a proporcionalidade. Observe:
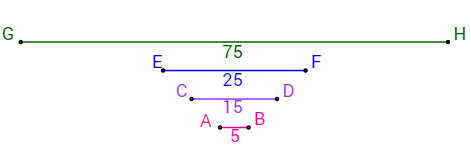
Nos segmentos acima, podemos observar a seguinte igualdade:
CD = GH = 3
AB EF
Logo, os segmentos CD, AB, GH e EF, nessa ordem, são proporcionais.
Portanto, dizemos que quatro segmentos (AB, CD, EF e GH) são proporcionais quando, respeitando determinada ordem, podemos escrever:
AB = EF
CD GH
No exemplo seguinte, utilizamos essa proporcionalidade para determinar a medida do quarto segmento.
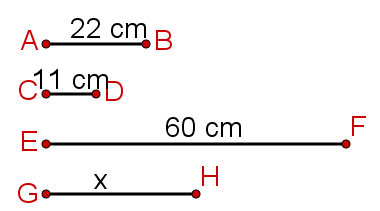
Exemplo – Sabendo que os segmentos AB, CD, EF e GH, nessa ordem, são proporcionais, determine a medida do segmento AB.
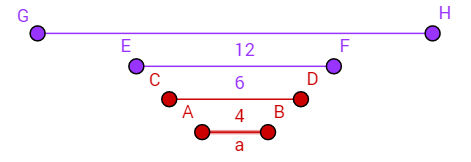
Conforme a ordem proposta pelo exercício, escreva a proporcionalidade:
AB = EF
CD GH
Substitua as medidas dos segmentos:
a = 6
4 12
12a = 24
a = 24
12
a = 2
Portanto, o segmento AB mede 2.
Por Luiz Paulo Moreira
Graduado em Matemática