PUBLICIDADE
A Geometria Espacial é a Geometria considerando três dimensões, ou seja, é a Geometria no espaço. Vivemos em um mundo tridimensional e estamos cercados de objetos geométricos, como os conhecidos sólidos geométricos, os poliedros, os corpos redondos, entre outros. Na Geometria Espacial é possível compreender melhor as formas geométricas que possuem três dimensões, uma vez que seus estudos são voltados a elas.
Leia também: Geometria Analítica — a Geometria que estuda as formas e sólidos geométricos com o auxílio da Álgebra
Tópicos deste artigo
- 1 - Resumo sobre Geometria Espacial
- 2 - O que a Geometria Espacial estuda?
- 3 - Conceitos importantes da Geometria Espacial
- 4 - Principais figuras da Geometria Espacial
- 5 - Principais fórmulas da Geometria Espacial
- 6 - Diferença entre Geometria Espacial e Geometria Plana
- 7 - Exercícios resolvidos sobre Geometria Espacial
Resumo sobre Geometria Espacial
-
A Geometria Espacial é o estudo de objetos geométricos no espaço, ou seja, em um universo tridimensional.
-
O ponto, a reta, o plano e o espaço são conceitos importantes para a Geometria Espacial.
-
Na Geometria Espacial estudamos os sólidos geométricos, como os poliedros e os corpos redondos.
-
Na Geometria Espacial existem fórmulas importantes envolvendo os sólidos geométricos, como o cálculo do volume e da área total.
-
Diferentemente da Geometria Espacial, a Geometria Plana estuda objetos no plano, ou seja, com duas dimensões. Ela é a base da Geometria Espacial.
O que a Geometria Espacial estuda?
A Geometria Espacial estuda as figuras espaciais conhecidas como sólidos geométricos. O cubo, o cilindro, o cone, as pirâmides, entre outros, são objetos de estudo da Geometria Espacial. Por meio da Geometria Espacial é possível descobrir as características e propriedades dos sólidos geométricos, e também é possível desenvolver fórmulas para o cálculo de volume e de área desses sólidos.
Conceitos importantes da Geometria Espacial
Para compreender a Geometria Espacial, é importante conhecer os elementos primitivos, que são: o ponto, a reta, o plano e o espaço. Os elementos primitivos são assim chamados por serem a base da Geometria e não possuírem uma definição, entretanto, todos temos uma intuição sobre cada um deles.
→ Ponto
Os pontos são representados por letras maiúsculas do nosso alfabeto e são o primeiro elemento primitivo da Geometria. O ponto não possui nenhuma dimensão, ou seja, é adimensional.
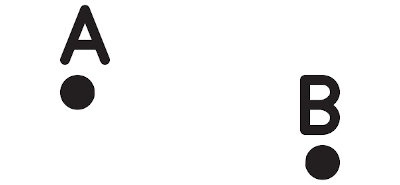
→ Reta
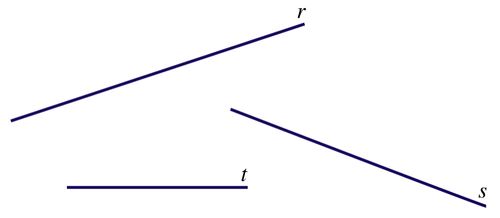
A reta é o segundo elemento primitivo, representado por letras minúsculas do alfabeto (por exemplo, r). A reta possui infinitos pontos colineares e uma única dimensão.
→ Plano
O plano é o terceiro elemento primitivo. Ele é representado por letras do alfabeto grego, como α, β, entre outras. O plano possui duas dimensões.
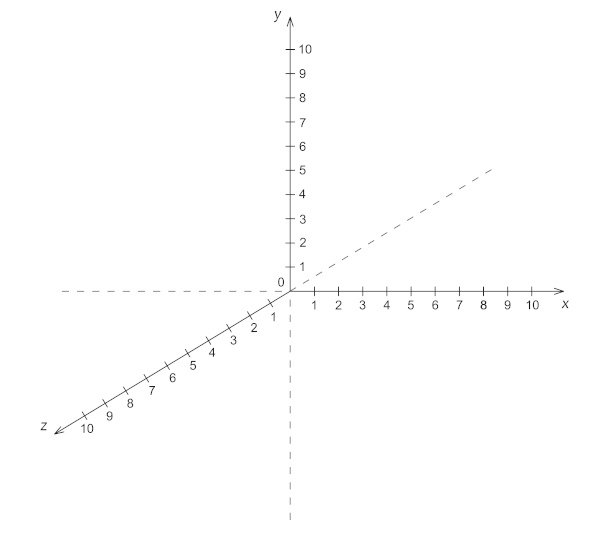
→ Espaço
O espaço possui três dimensões. Podemos representar o espaço quando temos três eixos reais, um para cada dimensão, como na imagem a seguir:
Veja também: Posição relativa entre reta e plano
Principais figuras da Geometria Espacial
As figuras da Geometria Espacial são conhecidas como sólidos geométricos. Os sólidos geométricos são divididos em dois grupos: os poliedros e os corpos redondos.
→ Poliedros
Os poliedros são os sólidos geométricos que possuem faces formadas por polígonos, como o cubo, as pirâmides e os prismas.
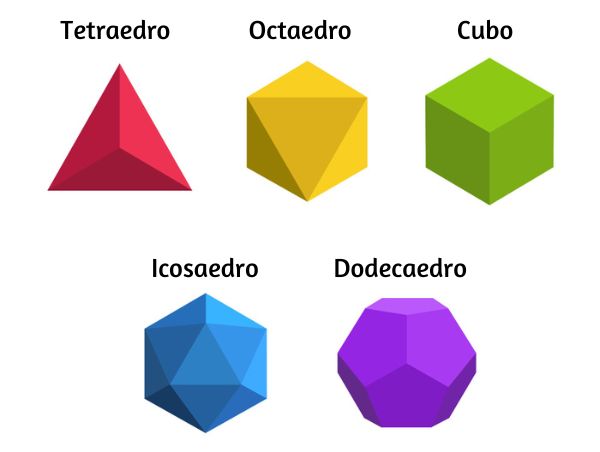
◦ Sólidos de Platão
Os sólidos de Platão são poliedros que possuem todos as faces congruentes. São classificados como sólidos de Platão o tetraedro, o hexaedro, o octaedro, o dodecaedro e o icosaedro. Todos esses cinco sólidos são poliedros regulares, ou seja, possuem arestas e faces congruentes.
→ Corpos redondos
Os corpos redondos são os sólidos geométricos que possuem formas arredondadas. Os principais corpos redondos são a esfera, o cone e o cilindro.
Principais fórmulas da Geometria Espacial
No estudo da Geometria Espacial são desenvolvidas fórmulas específicas para calcular o volume e a área total dos sólidos geométricos.
→ Fórmulas do prisma
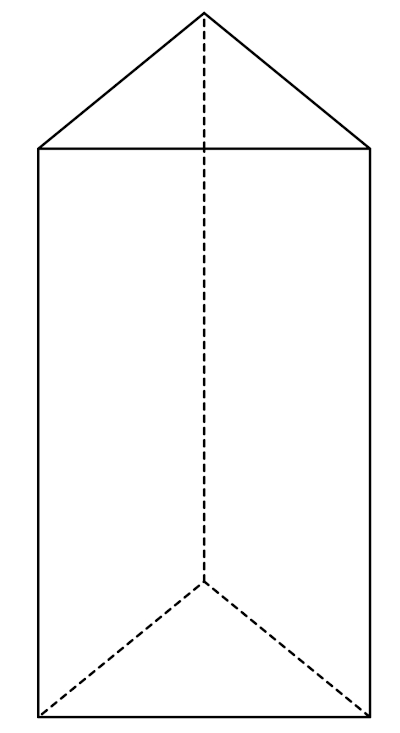
Para calcular o volume do prisma, é necessário conhecer a área da sua base e a sua altura. Já a área total do prisma é calculada utilizando a área da base e a área lateral. As fórmulas do volume, representado por V, e da área total, representada por \(A_t\), são:
V = Ab· h
At = 2Ab + Al
-
Ab → área da base.
-
Al → área lateral.
-
H → altura.
→ Fórmulas da pirâmide
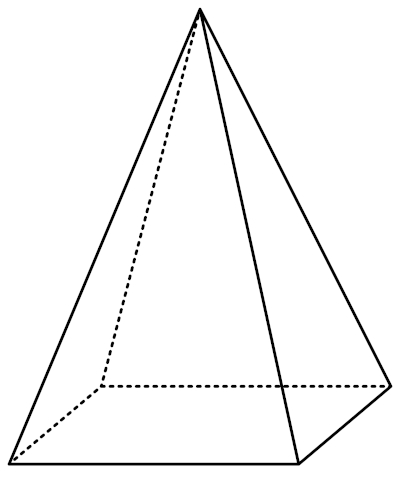
Assim como o prisma, as fórmulas de volume e área total da pirâmide dependem da sua área da base, da área lateral e da altura.
\(V=\frac{A_b⋅h}3\)
\(A_t=A_b+A_l\)
→ Fórmulas do cilindro
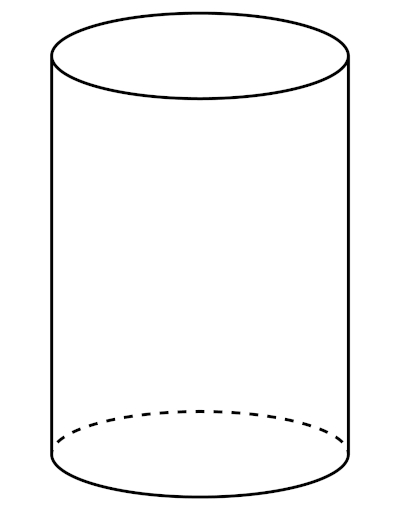
Para calcular o volume e a área total do cilindro, é necessário conhecer o comprimento da altura e do raio do cilindro.
V = πr² · h
At = 2πr (r + h)
-
r → raio.
→ Fórmulas do cone
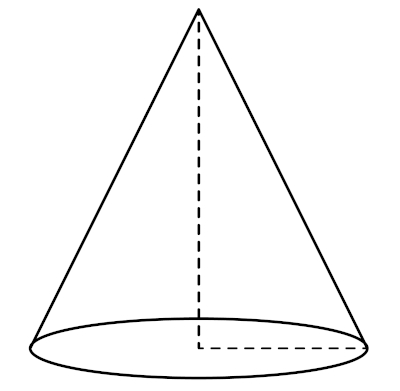
O cone, além da fórmula do volume e da área total, tem também a fórmula da geratriz, que relaciona seu raio e sua altura.
\(V=\frac{π⋅r^2⋅h}3\)
g² = r² + h²
At = πr (r + g)
-
g → geratriz do cone.
→ Fórmulas da esfera
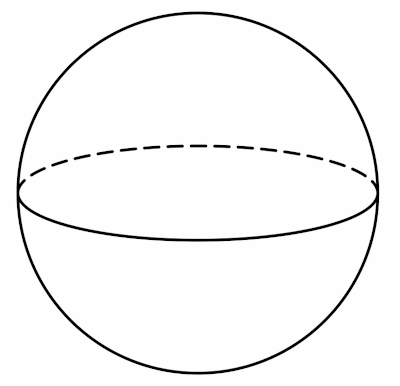
Para calcular o volume e a área total da esfera, é necessário conhecer somente o comprimento do seu raio.
\(V=\frac{4πr^3}3\)
At = 4πr²
Diferença entre Geometria Espacial e Geometria Plana
A diferença entre a Geometria Espacial e a Geometria Plana é que a Geometria Espacial é tridimensional e a Geometria Plana é bidimensional. Ambas possuem grande importância para o desenvolvimento da Geometria, e a Geometria Plana é base para a Geometria Espacial.
Exercícios resolvidos sobre Geometria Espacial
Questão 1
Das figuras geométricas as seguir, marque a alternativa que contém uma figura que não é espacial.
A) Pirâmide
B) Cilindro
C) Cubo
D) Circunferência
E) Prisma
Resolução:
Alternativa D
Nas alternativas, a única figura geométrica que não é espacial, ou seja, não possui 3 dimensões, é a circunferência.
Questão 2
(Enem 2011) A figura seguinte mostra um modelo de sombrinha muito usado em países orientais.
Esta figura é uma representação de uma superfície de revolução chamada de
A) pirâmide.
B) semiesfera.
C) cilindro.
D) tronco de cone.
E) cone.
Resolução:
Alternativa E
A superfície da sombrinha possui o formato de um cone.
Por Raul Rodrigues de Oliveira
Professor de Matemática
